想定読者
高階関数、カリー化、部分適用、クロージャ
などの言葉を目にするたび不安になってしまい
それぞれの意味を何度も調べてしまう人へ1。
カリー化の反対にあたる逆カリー化に焦点を当て、
もう忘れないように理解をまとめておきたい。
高階関数
引数もしくは戻値が関数であるとき
その関数を高階関数と呼ぶらしい。
const apply = f => x => f(x)
関数 apply は1引数関数 f を引数に取って
関数 x => f(x) を返すので高階関数と言える。
関数の関数という構造は何となく神秘的で
特別な名前を付けたくなる気持ちは分かる。
しかし、本質的に重要なのは
数値などと同じように関数を扱えること^first-class object
なのではないかと個人的には思う。
引数もしくは戻値が数値であるとき
その関数を数値関数と呼んでみよう。
const succ = n => n + 1
関数 succ は数値 n を引数に取って
数値 n + 1 を返すので数値関数と言える。
それはそうであると感じるのではないだろうか。
高階関数もその程度の理解で良いと思われる。
カリー化と逆カリー化
カリー化と逆カリー化は
変換と逆変換の関係に相当する。
変換してから逆変換すると元に戻る2。
カリー化とは元に戻せる変換である。
変換
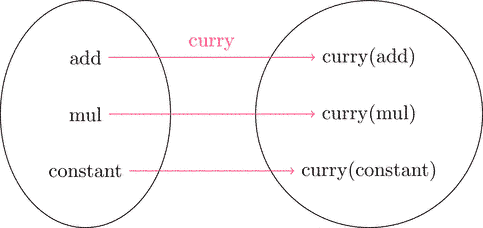
カリー化とは次のような変換のことだ。
const curry = f => x => y => f(x, y)
高階関数 curry は2引数関数 f を
高階関数 x => y => f(x, y) に変換する。
例として、次の2引数関数 add を考える。
const add = (x, y) => x + y
当然ではあるが add(2,3) $=$ 5 となる。
カリー化された高階関数 curry(add) は
同様に curry(add)(2)(3) $=$ 5 である。
逆変換
逆カリー化とは次のような逆変換のことだ。
const uncurry = g => (x, y) => g(x)(y)
高階関数 uncurry は高階関数 g を
2引数関数 (x, y) => g(x)(y) に逆変換する。
例として、次の高階関数 add を考える。
const add = x => y => x + y
当然ではあるが add(2)(3) $=$ 5 となる。
逆カリー化された2引数関数 uncurry(add) は
同様に uncurry(add)(2, 3) $=$ 5 である。
変換と逆変換
再び例として、次の2引数関数 add を考える。
const add = (x, y) => x + y
変換 curry と逆変換 uncurry に対して
add(2, 3) $=$ uncurry(curry(add))(2, 3) $=$ 5
が成り立つことを確認できるだろう。
これは任意の引数 (x, y) に対して成り立ち、
add $=$ uncurry(curry(add)) である3。
任意の2引数関数 f に対して、
カリー化された関数 curry(f) は
逆変換 uncurry で元の関数 f に戻せる。
const add = (x, y) => x + y
const mul = (x, y) => x * y
const constant = (x, _) => x
変換により f と curry(f) は1対1対応する。
部分適用
部分適用とは次のような変換のことだ。
const papply = (f, x) => y => f(x, y)
高階関数 papply は2引数関数 f と引数 x の
組 (f, x) を1引数関数 y => f(x, y) に変換する。
例として、次の2引数関数 mul と constant を考えよう。
const mul = (x, y) => x * y
const constant = (x, _) => x
第1引数に 0 を部分適用すれば以下となる。
const mul0 = papply(mul, 0)
const constant0 = papply(constant, 0)
この関数 mul0 は全てを 0 にする。
[1, 2, 3].map(mul0) $=$ [0, 0, 0]
また関数 constant0 も全てを 0 にする。
[1, 2, 3].map(constant0) $=$ [0, 0, 0]
上記の関数 mul0 と constant0 は
変換 curry を用いて次のようにも書ける。
const mul0 = curry(mul)(0)
const constant0 = curry(constant)(0)
変換 papply と curry は、確かに似て見えて、
同じことをしていてるように感じるかもしれない。
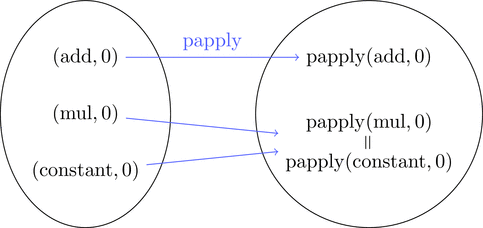
ここで注目すべきは mul0 や constant0 を
元の (mul, 0) や (constant, 0) に戻せるかどうかだ。
関数 mul0 と constant0 は全てを 0 にする。
つまり mul0 $=$ constant0 であることに注意しよう。
例えば部分適用された関数 mul0 の逆変換を試みても、
(mul, 0) と (constant, 0) のどちらに移せば良いか
分からないため、元の (mul, 0) に戻せない。
const add = (x, y) => x + y
const mul = (x, y) => x * y
const constant = (x, _) => x
変換と逆変換で見たような1対1対応こそが
元に戻せるという性質をあらわしている。
クロージャ
環境とラムダ式(アロー関数)の両者を
合わせたものをクロージャと呼ぶらしい4。
{
let a = 2
let b = 1
const closure = x => a*x + b
}
関数 closure の中では宣言されておらず
外の環境で宣言されているような変数 a と b を
関数の宣言時に閉じ込めるイメージだろうか。
変数 a と b をグローバル変数だと思えば、
次のような関数もクロージャと考えられるだろう。
const closure = x => a*x + b
変数の数はいくつでも良いと思うので、
たまたま0個な次のような関数もクロージャだろう。
const closure = x => 2*x + 1
クロージャと関数を同一視してしまっても
実用上はなんの問題もないような気がする。
と思っていたけれど、例えば Rust においては
関数ポインタ型 fn() とクロージャ型 Fn() の
区別を意識する必要がありそうだ5。
コンパイラの気持ちになってみれば、
実行前に内容がある程度分かる関数ポインタ型と
環境に応じて内容が変わるクロージャ型を
同一視されると困るというのは分かる気もする。
狭義には次のような高階関数 enClosure の戻値
すなわち関数 closure をクロージャと呼ぶだろう。
const enClosure = (a, b) => {
const closure = x => a*x + b
return closure
}
これを次のように書けば、単なる高階関数に見える。
const enClosure = (a, b) => x => a*x + b
やはりクロージャと関数を同一視しても良さそうだ。
クロージャの例としてよく見るカウンターを考えよう。
const newCounter = count => {
const counter = del => {
count = count + del
return count
}
return counter
}
これまでと異なり変数 count は可変だが、
高階関数 newCounter の戻値 counter を
クロージャと呼んでいるに過ぎないだろう。
少し苦しいが次のように書けば、単なる高階関数だ。
const newCounter = count => del => count = count + del
クロージャとは関数だと理解しておくことにする。
そのほうが覚えるべきことが減って簡単なはずだ。
まとめ
カリー化と部分適用の違いについては
分かりやすい解説がたくさんあるけれど、
特に1対1対応を重視したような解説は
見つけることができなかったので書いてみた。
タイトルに関しては次記事のリスペクトです。
「食べられないほうのカリー化入門」(2013-07-22)
食べ物のカレーを元の材料には戻せないので、
元に戻せるかどうかでもカレー化とカリー化の
両者を区別することが可能だと思いました。