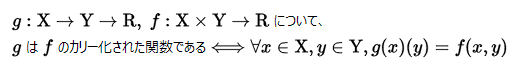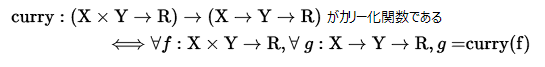『カリー化』(Currying) という概念をご存知でしょうか。"Curry" は食べ物のカレー(Curry)と同じスペルですが、ここでいう Curry はそれとは別のもので、多くのプログラミング言語に応用できるかもしれない、とても便利かもしれない概念です。
では教えてくれ。”カリー化”とはなんのことだ?
『ふたつの引数のうち、大きい方の数を返す』という機能を持った関数 max を実装したいとしましょう。そのようなとき、大抵は次のように定義すると思います。
function max(x, y){
return x > y ? x : y;
}
しかしながら、次のように定義した別の関数 _max でも同じような機能を実現することができます。
function _max(x){
return function(y){
return x > y ? x : y;
}
}
この関数 _max も『大きい方の数を返す』という機能を持っていますが、_max は max とは呼び出し方が少し異なります。たとえば、_max で 1 と 2 のうち大きい方を求めるには、 _max(1)(2) のように書きます。
_max が通常の max と異なるところは、関数を呼び出すときに引数をひとつづつ渡すようになっているところです。引数をひとつ渡すと、『引数をもう一つわたすと、最初に渡した引数と今渡された引数のうち大きいほうを返す関数』を返すようになっているのです。括弧が増えるぶんソースコードはいくらか長くなりますが、呼び出し方が異なるだけで目的とする機能が実現できていることには違いはありません。このように、『2引数以上の関数を、1引数の関数の定義だけで同じ機能を持つように定義を書き換えること』を カリー化 といいます。もちろん2引数に限らず、引数の数がそれ以上であってもカリー化することは可能です。
カレーがシャッキリポンとコード上で踊るわ!
さて、わざわざこんな妙な関数の定義をして、いったい何が嬉しいんでしょうか?プログラミングにおけるカリー化のメリットのひとつとして、 カリー化された関数に引数を渡すだけで、べつの機能を持つ関数を簡単に作り出せる 、というものがあります。
たとえば、配列 brightness に画像の各ピクセルの明るさが格納されていて、いくつかの画像処理の結果、要素に負の数の要素が現れるようになったとしましょう。明るさは 0.0~1.0 の範囲で、明るさが 0 より小さくなってはまずいので 0より小さい値は 0 に変えたいとします。配列のすべての要素に関数を適用する関数 Array.prototype.map を利用して実装することにすると、map に『0より小さい値は 0 に変える』というような関数を渡せばいいでしょう。 でもそのような関数はないので、無名関数を使って次のように定義することになると思います。
var brightness = [0.2, -0.3, 1.0, -0.5];
brightness = brightness.map(function(x){ return max(0, x) });
上のコードの function(x){ return max(0, x) } という式は、『引数をもう一つわたすと、0 と今渡された引数のうち大きいほうを返す関数』という関数を表しています。そういえば、先ほど定義した _max は、引数を渡すと『引数をもう一つわたすと、最初に渡した引数と今渡された引数のうち大きいほうを返す関数』を作ってくれる関数でした。それなら、_max(0) は『引数をもう一つわたすと、0 と今渡された引数のうち大きいほうを返す関数』を返してくれるはずです。つまり、無名関数を使わずとも _max を使うと次のように書きなおせることがわかります。
var brightness = [0.2, -0.3, 1.0, -0.5];
brightness = brightness.map(_max(0));
function 式もなくなって、とてもシンプルになりました!このように、関数リテラルで function(x){ return max(0, x) } のような面倒な記述をしなくても、カリー化された関数なら引数を渡すだけで別の関数を簡単に作り出せるのです。
なるべく手をかけず簡単に。これが美味しいカレーを作るこつです
さて、先程は max を手作業でカリー化された形式 _max を定義しなおしたわけですが、いくらカリー化された関数にメリットがあるとしても、関数を定義するたびに先ほどのように function 式を入れ子にして書くのはなかなか面倒です。なんとか関数を簡単にカリー化できないものかと、カリー化を行う関数 curry を次のように定義してみました。
function curry(f){
return function _curry(xs){
return xs.length < f.length ? function(x){ return _curry(xs.concat([x])); } : f.apply(undefined, xs);
}([]);
}
この関数 curry を使えば、さきほどの max のような関数や、一部の標準ライブラリ関数などを簡単にカリー化することができます。たとえば、次のように標準ライブラリの Math.max をカリー化することで _max を定義できます。
var _max = curry(Math.max);
したがって、先ほどの画像処理のプログラムも、curry を使えば次のように書くことができます。
var brightness = [0.2, -0.3, 1.0, -0.5];
brightness = brightness.map(curry(Math.max)(0));
このカレーはできそこないだ。食べられないよ
さて、カリー化されていない関数でも curry に通すだけで簡単にカリー化できるようにはなりましたが……果たしてコレ、役に立つんでしょうか?既存の関数はもちろんカリー化されていないので、map や filter のような関数にはいちいち curry を呼び出してから渡す必要があります。記述は多少短くなったものの、curry を呼ぶ手間に関してはどうしようもありません。また、場合によっては curry の呼び出しやカリー化された関数の呼び出しのオーバーヘッドも無視できません。カリー化のメリットが最も発揮されるのは、
- 通常の方法で定義された関数は、すべてカリー化されている
- 関数適用の構文がシンプル
- 高階関数を多用する API が用意されている
という条件が揃った時だと思います。言語そのものにカリー化の機能があればとても便利ですが、そうでない言語において curry のような関数を持ち込んでも、結局のところ curry の呼び出し自体を取り除くことはできませんし、あまり標準的なコーディングでない方法を持ち込むことで他の人にコードが読みにくいと言われるかもしれません。多少コードが冗長になったとしても、カリー化しないで標準的な function 式を使うコーディングを使ったほうがいいかもしれません。
じゃあカリー化がちゃんと活躍している言語にはどんなものがあるかというと、Haskell や OCaml が挙げられます。Haskell では先程の画像処理のプログラムを次のように書くことができます。
brightness = [0.2, -0.3, 1.0, -0.5]
brightness' = map (max 0) brightness
このとき、
-
maxは Haskell 組み込みの関数で、最初からカリー化された形式で定義されています。関数を普通に定義すると、それは自動的にカリー化された関数になります。 - 関数適用の構文は、
max 0 1のように関数の後ろに空白で区切って引数を書くだけなので、普通に呼び出しても括弧だらけになったりしません - リストの各要素に関数を適用して別のリストに写す
mapを始め、このような高階関数(関数を引数にとったり関数を返す関数)がごく当たり前の手法として用いられています。for 文などは最初から存在しません。
これを考えると、JavaScript にカリー化を持ち込んで味わえる旨味というのは、Haskell で味わえる旨味には及ばないと言わざるを得ないのです。残念……。
このカレーを作ったのは誰だあっ!!
カリー化(Currying) の "Curry" は食べ物のカレーとスペルがまったく同じですが、カリー化は食べ物とは関係なくて、この辺りの分野に大きな業績のある論理学者・数学者のハスケル・カリー(Haskell Curry)さんの名前に由来します(そうです、Haskell もこのひとの名前に由来しています)。でもWikipedia によれば、最初にカリー化の概念を示したのは Moses Schönfinkel さんとゴットロープ・フレーゲさんだそうな。自分は Schönfinkel さんは失礼ながらご存じあげないのですが、フレーゲさんは論理学者としてとても有名な方ですよね。カリー化はプログラミング特有の概念というわけではなく、もともと数学で関数の振る舞いを調べるときに便利なように考案されたものみたいです。
やれやれ。こんな部分適用をカリー化と言っているようじゃ、ほんとに理解しているのか怪しいもんだ
複数の引数をもつ関数に、一部だけ引数を渡して呼び出すことを関数の 部分適用 といいますが、カリー化は関数の部分適用とよく混同されるようです。一部の言語において実際には部分適用を行う関数に何故か curry という名前を付けてしまったものが存在し、それがさらに混乱を招いているということもあるようです。確かにカリー化と部分適用は非常に近しい関係にありますが、あくまで両者は似て非なるものです。せっかくですので、カリー化と部分適用の違いについて正確に理解しておきましょう。
自然言語でいろいろと説明を尽くすのも大事なことですが、正確な理解のためには形式的な定義に勝るものはありません。カリー化を形式的にいうと、次のようになります。簡単のためここでは2引数の関数についてのみ述べますが、3引数以上の関数でも同じように議論できます。( 数式を読むのが面倒臭いひとは、結論だけ読んでください )
また、
関数 f を curry に適用するだけでカリー化された関数 g に変えてくれるわけですね。
それに対し、部分適用はというと、
この操作 partial(f, x) を関数の 部分適用 といいます。関数 f に x を部分適用した式 partial(f, x) は、残りの引数を渡すと普通に f にすべての引数を渡したのと同じように計算してくれます。あくまで f は2引数の関数ですが、そのうち最初の 1 つの引数だけを適用しているようになっているので『部分』適用と呼ぶわけです。
最後に、カリー化関数 curry と部分適用関数 partial の関係を形式的に表してみましょう。
『f に x を部分適用する』というのは、『 f をカリー化してから x を適用する』のとおなじだ、というわけです。したがって、『f に x を部分適用する』というのは、『 f をカリー化する』のとは異なります。これで部分適用 partial(f, x) とカリー化 curry(f) の違いがおわかり頂けたのではないでしょうか。