はじめに
- 自己紹介:UbuntuでPythonを書いてデータ分析とか異常検知してます。
- Twitterやってます。
- AutoMLの一分野であるNAS(Neural Architecture Search)に興味があります。
- NASのブームのきっかけであるNAS with RL(Zoph and Le, 2017)を抄訳&解説しました。
- この論文を読もうと思った理由:NASのブームのきっかけだから
- リンクはこちら
簡単にまとめ
- NNの構造と重みを自動で最適化するNASという研究分野の論文
- pros:既存のNAS手法&ハンドクラフトのNNより性能が出た
- cons:計算量が高すぎる
- 面白いなと思ったところ
- 微分不可能な目的関数を、方策勾配法で最適化
- LSTMの出力をNNのハイパラと見なす
- AttentionでSkip connect等を表現すれば誤差逆伝播可能
ABSTRACT
- NNを人力で設計することは非常に大変です。
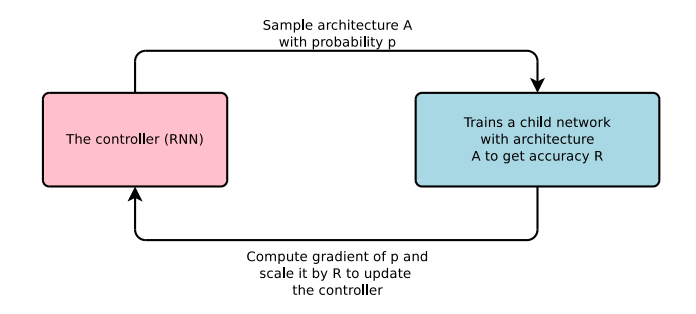
- 本論文では、RNNを使って最適化したいNNを生成します。
- このRNNをController、最適化したいNNをChild Networkと呼びます。
- Child Networkのvalidデータでの精度を報酬として、Contollerを強化学習でtrainします。
- これを繰り返してChild Networkを最適化します。
- 2種類の実験を行いました。(1)CNN:CIFAR-10で分類 (2)RNN:PTBで言語モデリング
- 両方共よい結果が出ました。 (1)Test error:3.65% (2)Perplexity:62.4
1. INTRODUCTION
- DNNの登場によって、特徴量設計からNNの構造設計にパラダイムシフトが起こりました。
- それでも、タスクに応じたNNの構造設計は難しいです。
- 私達はNNの構造は可変長の文字列で表すことができるという所に着目しました。
- その可変長の文字列を生成するRNN(Controller)を考えます。
- Contorollerの出力(可変長の文字列)からChild Networkを生成し、Child Networkを学習させます。
- タスクを解かせ、その精度を報酬にしてControllerを方策勾配法で学習…を繰り返します。
- これによって、優れたNNモデルを0から作る事が出来ます。
2. RELATED WORK
- 既存のHPO(Hyperparameter optimization)は固定長の空間しか探索できません。
- だからNNの構造(レイヤは何層?ノードは何個?とか)と接続(Skip connectする?とか)を表現できません。
- ベイズ最適化は可変長の空間を探索できますが、本手法より柔軟ではありません。
- 進化的アルゴリズムも可変長の空間を探索できるし、柔軟ですが、本手法より計算コストがかかります。
- これらはsearch-basedな手法なので、ちゃんと動かしたかったらヒューリステックが必要という欠点もあります。
- Controllerはauto-regressiveです。つまり、過去の予測を元に予測を行います。
- そういう意味ではSeq2Seqに似ています。
- 本手法とSeq2Seqとの違いは、微分不可能なMetric(Child Networkの精度)を最適化するという点です。
- そういう意味では機械翻訳におけるBLUE最適化に似ています。
- 本手法とBLUE最適化との違いは、教師有り学習ではなく強化学習を行っている点です。
- メタ学習の考え方も参考にしています。
- 重要な参考文献は以下の2点です。
- NNを用いて、別のNNを勾配降下法で更新する(Andrychowicz et al., 2016)
- 強化学習を用いて、アルゴリズム設計を自動化する(Li & Malik, 2016)
3. METHODS
- 本セクションでは以下の4点について説明します。
- Controller(RNN)でCNNを生成する方法
- Child Networkの精度を報酬として、方策勾配法でControllerを学習する方法
- Core approach : 学習速度を上げる手法と、Child Networkの表現力を高める手法
- key contribution : RNNを生成する方法
3.1 Controller(RNN)でCNNを生成する方法
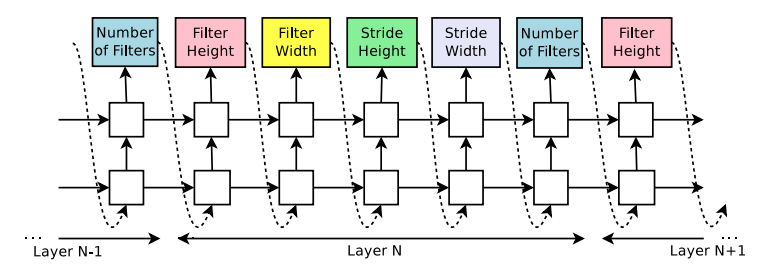
- Figure 2は、RNNがCNNのハイパーパラメータを生成する様子です。
- 出力されたトークン(Filter Heightなど)は、CNNのN層目のハイパーパラメータを示しています。
- 本実験では、Controllerの学習につれレイヤ数を増やし、しきい値を超えると終了するように設定しました。
- Controllerの学習が終わった後、そのトークンで表されるCNNが生成され、trainデータで学習を行います。
- CNNの学習が終わった後、validデータで精度を記録します。
- Controllerの方策パラメータ$\theta_c $を、Child Networkの精度が最大になるよう最適化します。(次節で解説)
3.2 方策勾配法でControllerを学習する方法
- Controllerの出力は、強化学習の文脈において、Child Networkを生成する行動 $a_{1:T}$のリストとみなせます。
- Child Networkの精度$R$を報酬とすると、予想される報酬は $J(\theta_c)=E_{P(a_{1:T}; \theta_c)}[R]$で表せます。
- ここで、$T$はControllerが出力するハイパーパラメータの総数です。
- $R$は$\theta_c$で微分不可能なので、方策勾配法の一種であるREINFORCEアルゴリズム(Williams, 1992)で$J(\theta_c)$を求めます。
$$\nabla_{\theta_c}J(\theta_c) = \sum_{t=1}^{T}E_{P(a_{1:T}; \theta_c)}[\nabla_{\theta_c}\log P(a_t\mid a_{(t-1):1};\theta_c)R]$$ - 1個のControllerからm個のChild Networkをサンプルします。
- k番目のChild Networkの精度(報酬) $R_k$を用いて、以下のように近似できます。
$$\frac{1}{m}\sum_{k=1}^{m}\sum_{t=1}^{T}\nabla_{\theta_c}\log P(a_t\mid a_{(t-1):1};\theta_c)R_k$$
- さらに、勾配の推定値の分散を減らすために、ベースライン関数 $b$を用いて近似し直します。
$$\frac{1}{m}\sum_{k=1}^{m}\sum_{t=1}^{T}\nabla_{\theta_c}\log P(a_t\mid a_{(t-1):1};\theta_c)(R_k-b)$$ - 本論文では、$b$として以前のChild Networkの精度の指数移動平均を用います。
解説
方策勾配法:時間ステップ$t$で、目的関数の方策パラメータ$\theta$に関する確率勾配$G_t$を用いて$\theta$を更新する手法。
環境が未知の場合、目的関数はblackboxであり$G_t$が計算出来ないため推定する必要がある。
ここで、差分行動価値関数$Q_\infty^{\pi}$とその推定値$\hat{Q_t}$を用いて$G_t$は以下のように表すことができる。
証明は強化学習(森村, 2019)6章3節を参照。
$Q_\infty^{\pi}$は期待累積報酬で、通常の行動価値観数$Q$と異なり、時間割引がない。
代わりに、報酬から平均報酬を引くことで発散を防いでいる。
$$G_t = \nabla_{\theta_c}\log \pi_\theta(a_t\mid s_t)(\hat{Q_t}-b(s_t)) $$
$Q_\infty^{\pi}$の推定にモンテカルロ標本を用いるのが本論文で登場したREINFORCE法。
モンテカルロ標本 : 確率的に入力を与えて得るサンプル。
他にはクリティックで$Q_\infty^{\pi}$を近似・推定するアクター・クリティック方策勾配法などもある。
つまり、REINFORCE法は方策勾配法の1種であり、期待累積報酬にモンテカルロ標本を用いる手法。
REward Increment=Nonnegative Factor times Offset Reinforcement times Charactaristic Eligibilityの頭文字。
即時報酬$r$による$\theta$の微小変化を、非負の学習率 * オフセットした即時報酬 * 更新前の$\theta$の適格度 で表す。
$$ \Delta \theta = \alpha*(r-b)*e_t$$
オフセット : ベースライン$b$を用いて勾配の推定の分散を小さくする事。$b$として平均報酬の推定値が使われる事が多い。
適格度は以下のように変形できる。
$$e_t = \nabla_{\theta}\log \pi(a_t\mid s_t,\theta) = \nabla_{\theta}\log P(a_t,s_t) = \frac{1}{P(a_t,s_t)} \frac{\partial P(a_t,s_t)}{\partial \theta}$$
またNNの重み$W$を用いて、以下の式が成り立つ。
$$(r-b) * e_t = \frac{\partial E[r \mid W]}{\partial \theta}$$
つまり適格度とはNNの重みが与えられた際の即時報酬の期待値の微分と、即時報酬の比であると言える。
本節のまとめ
- 期待報酬$J(\theta_c)$を最大化するよう、$\theta$を学習する。
- 方策勾配法の一種であるREINFORCEを用いた。
- 具体的には、$\nabla_{\theta_c}J(\theta_c)$をモンテカルロ標本を用いて、$\theta$の近似式で表した。
参考資料
- REINFORCE(Williams, 1992) 4章
- 「これからの強化学習」勉強会#2 P8
- ゼロから始める深層強化学習(NLP2018講演資料) P43~47
- 強化学習(森村, 2019) 6章
3.3 Core approach
3.3.1 学習速度を上げる手法
- $\theta_c$を更新する度に、数時間かけてChild Networkを学習させる必要があります。
- その為、分散学習と非同期パラメータ更新を用いてControllerの学習速度を向上させました。
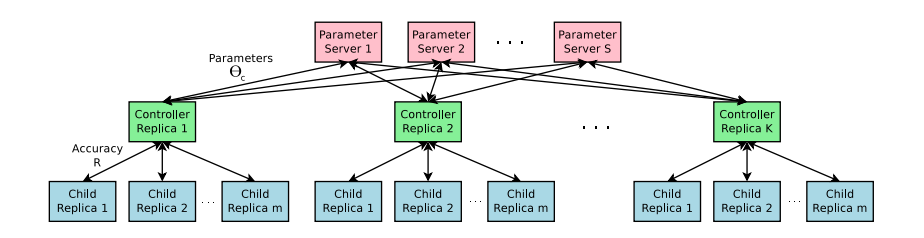
Figure 3 : 分散学習のイメージ。 - S個のパラメータサーバがK個のControllerの$\theta$をシェアします。
- 各Controllerはm個のChild Networkをサンプルし、それらはパラレルに学習されます。
- 本実験では、Child Networkのエポック数がしきい値に達すると学習を終了するよう設定しています。
3.3.2 Child Networkの表現力を高める手法
- セクション3.1のFigure 2では、Controllerを用いてバニラCNNを出力できる事を示しました。
- 本セクションでは、Skip connectionやBranchレイヤなどを生成する方法について説明します。
- これらによって、GoogleNetやResNetの様な、表現力の高いCNNを生成することが出来ます。
- 本論文ではAttentionの一種であるSet-selection type attention(Neelakantan et al., 2015)を用いました。
- 層ごとにアンカーポイントを設け、1〜N-1層目のアンカーポイントと確率的に接続します。
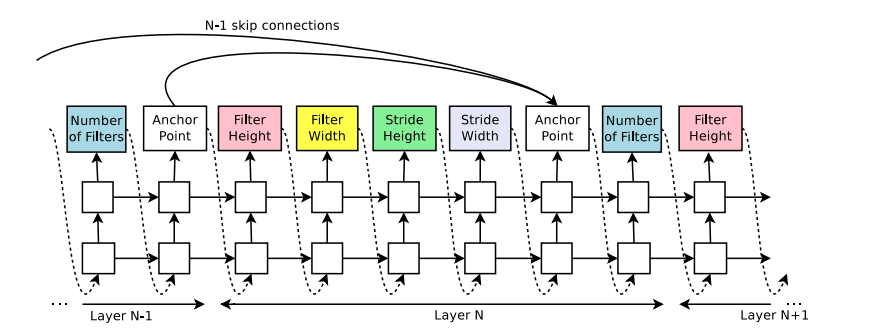
Figure 4 : 層ごとにアンカーポイントを設け、Skip connectを表現可能にしたController。
- 層間が伝播する確率はシグモイド関数で表現します。
- N層目の隠れ状態を$h_N$、Child Networkの学習パラメータ$v, W$を用いて以下の式で表すことが出来ます。
$$P(j層目の出力がi層目に入力される)=sigmoid(v^{T}tanh(W_{prev}* h_j + W_{curr} * h_i))$$
- 確率的な接続があってもREINFORCEアルゴリズムは適用可能です。
- 本実験では、N層目に複数層から入力があった場合、チャンネル方向にConcatnateするように設定しました。
- 接続を確率的に表現した場合、ある層への入出力がなくなってしまう場合があります。
- また、サイズが違う場合Concatenateできないという問題も有ります。
- それらを防ぐため、3つのルールを設けます。
- どの層からも入力がない層がある場合、最初のイメージを入力します。
- どの層にも出力されない層がある場合、最後の層に接続します。
- サイズが違う場合、0埋めでサイズを合わせてConcatenateします。
- 以上、Skip connectを実現する手法を紹介しました。
- Controllerにステップを追加し、学習率・プーリング層・Local contrast norm・Batch normなども表現可能です。
3.4 key contribution:RNNを生成する方法
-
本セクションではChild NetworkとしてRNNを生成する手法について説明します。
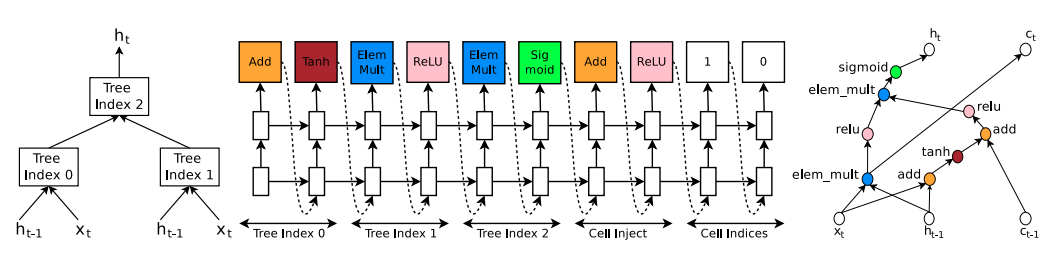
Figure 5 : RNNを生成する方法の一例。 -
RNNはタイムステップ$t$において、入力$x_t$と直前の隠れ状態$h_{t-1}$を受けとります。
$$h_t = tanh(W_1 * x_t + W_2 * h_{t-1})$$ -
さらに、LSTMは次のタイムステップに渡すセル$c_t$を保持します。
-
Figure 5 左図は、$h_{t-1}$と$x_t$から$h_t$が計算される流れをTreeで表したものです。
-
Tree Index0, 1, 2において、Combination→Activationの演算(2入力1出力)が行われます。
-
Combinationの例としては、Addやアダマール積があります。
-
Activationの例としては、TanhやSigmoid、ReLUがあります。
-
Figure 5 中央図の「Tree Index 0〜2」に注目して下さい。
-
左のステップでCombinationを、右のステップでActivationを選択しています。
-
$c_{t-1}$を入力とする演算はFigure 5 中央図の「Cell Inject」で行われています。
-
$c_t$を出力する演算はFigure 5 中央図の「Cell Indices」で行われています。
-
Figure 5 における演算の流れは以下の通りです。
Tree Index 0 の出力 $a_0 = tanh(W_1 * x_t + W_2 * h_{t-1})$
Tree Index 1 の出力 $a_1 = ReLU((W_3 * x_t) \otimes (W_4 * h_{t-1}))$
$a_0$と $c_{t-1}$の演算の結果 $a_0^{new} = ReLU(a_0 + c_{t-1})$ ←ここには学習パラメータはない
Tree Index 2 の出力 $a_2 = sigmoid(a_0^{new} \otimes a_1)$
定義から $h_t = a_2$
Cell Indexの左のステップにおいて どのTree Indexのcombinationを$C_t$にするか決める
Figure 5 では1が出力されている。つまり $c_t = (W_3 * x_t) \otimes (W_4 * h_{t-1})$ -
Figure 5 では2個のLeaf nodeを持つTreeを表していますが、本実験では8個のLeaf nodeを使用しました。
解説
LSTMでは、$c_{t-1}$、$h_{t-1}$、$x_t$を受け取って$h_t$、$c_t$を出力する。
本論文においては、$h_t$をsoftmaxに通して得られたトークンが$x_{t+1}$になる。
Figure 5 左図では、$c_t$と$c_{t-1}$を無視してTreeが描かれているが、
実際にはTree Index 0と2の間に$c_{t-1}$との演算(Add→ReLU)が行われている。
Figure 5 では、以下を仮定している。
$x_t$と$h_{t-1}$を入力とする演算は2種類(種類数は選べる)
→結果として「Add→Tanh」と「アダマール積→ReLu」になった
$c_{t-1}$を入力とする演算は1種類(自明)
→「Add→ReLU」になった
$c_t$を出力する演算は1種類(自明)
→「アダマール積→Sigmoid」になった
だからFigure 5 左図においてLeaf nodeは2個しかない。
論文の実験では8個のLeaf nodeを考えている。
つまり$h_{t-1}$と$x_t$を入力とする演算の組み合わせが8種類あるということ。
4. EXPERIMENTS AND RESULT
- 「CNNを設計し、CIFAR-10で画像分類」と「RNNを設計し、PTBで言語モデリング(と転移学習)」の2種類の実験をしました。
4.1 CNNを設計し、CIFAR-10で画像分類
Dataset : CIFAR-10、Data Arg、白色化、アップサンプリング→32*32にクロップ、水平フリップ
Search space : バニラCNN+ReLU、Batch norm、Skip connect。フィルタサイズは[1, 3, 5, 7]、フィルタ数は[24, 36, 48, 64]、ストライドは[1固定, [1, 2, 3]]、プーリングは[無し, Controllerの13・24層目に入れる]。
Controller : 隠れユニット35個の2層LSTM、Optimizer=ADAM、LR(Learning Rate)=0.0006、重みは-0.08〜0.08で初期化。
分散学習 : パラメータサーバ数$S=20$、Controller数$K=100$、ControllerあたりのChild Netrowk数$m=8$。
学習条件 : CNNの学習は50epochsで終了、直近5epochsのvalidデータでの精度をRとする。validはランダムに選んだ5000サンプル。1600サンプルごとにCNNの深さを2ずつ増やすように設定。(つまりControllerの隠れユニットは14ずつ増える)
詳細条件 : DenseNet(Huang et al. 2016)と同じ(Optimizer=Momentum、LR=0.1、momentum=0.9、weight decay=0.0001)。
本条件で学習終了後、CNNの構造を固定して、LR、WD、Batch normの $\epsilon$、LRを減衰させるepoch数についてグリッドサーチ探索し、testデータでの精度を計算する。
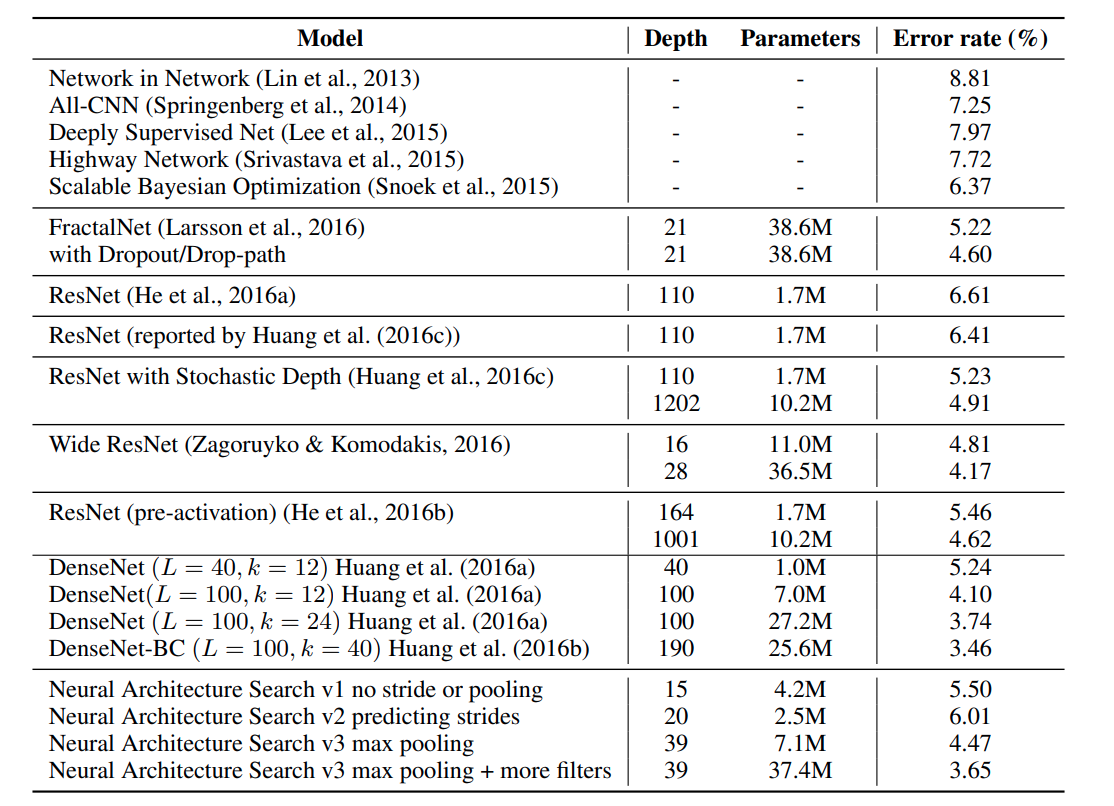
Table 1 : NASで探索したCNN4種類のCIFAR-10の精度、層数、パラメタ数
v1 : ストライド無し・プーリング無し(構造は6. APPENDIXに記載)
v2 : ストライド[1, 2, 3]・プーリング無し
v3 : ストライド[1, 2, 3]・プーリング有り
v4 : ストライド[1, 2, 3]・プーリング有り・フィルタ数を[6, 12, 24, 36]に変更・手動で40個のフィルタを追加
解説
Controllerは隠れユニット35個の2層LSTM。
バニラCNN(フィルタサイズの縦横、ストライドの縦横、フィルタ数5種)+Batch norm、Skip connectのアンカー2種なので、CNN1層あたり7隠れユニットが対応している。
つまり、$\frac{35}{7}+1 = 6$ なので6層CNNから探索を始めている。
$\frac{45000}{1600}$ = 28.125なので、CNNの学習終了時には6 + 28 * 2 = 62層CNNまで探索している。
1600サンプルごとにCNNの構造を変更しているので、合計$K * m * 1600 = 12800$種類のCNNを探索する。
4.2 RNNを設計し、PTBで言語モデリング(と転移学習)
Dataset : PTB。小さいデータセットのためoverfit対策が必須。Dropoutを用いる。Shared embeddings(入出力のembeddingに同じ重みを用いることで精度を向上させる手法。weight tyingとも呼ばれる。)を用いる。
Search space : Combinationは[Add, アダマール積]、Activationは[identity, tanh, sigmoid, ReLU]。よって組み合わせは8通り。
学習条件 : Child Networkの学習は35epochsで終了、$\frac{80}{{perplexity}^2}$をRとする。
その他の設定は、以下の3点を除き、セクション4.1のCNNの実験と同じ。(1)Controllerの学習率は0.0005。(2)分散学習について、S=20、K=400、m=1。400個のControllerを400個のCPUで同時に学習させた。 (3)Controllerの非同期学習では、10回目的関数の勾配を受け取ったらパラメータ$\theta$を更新する。
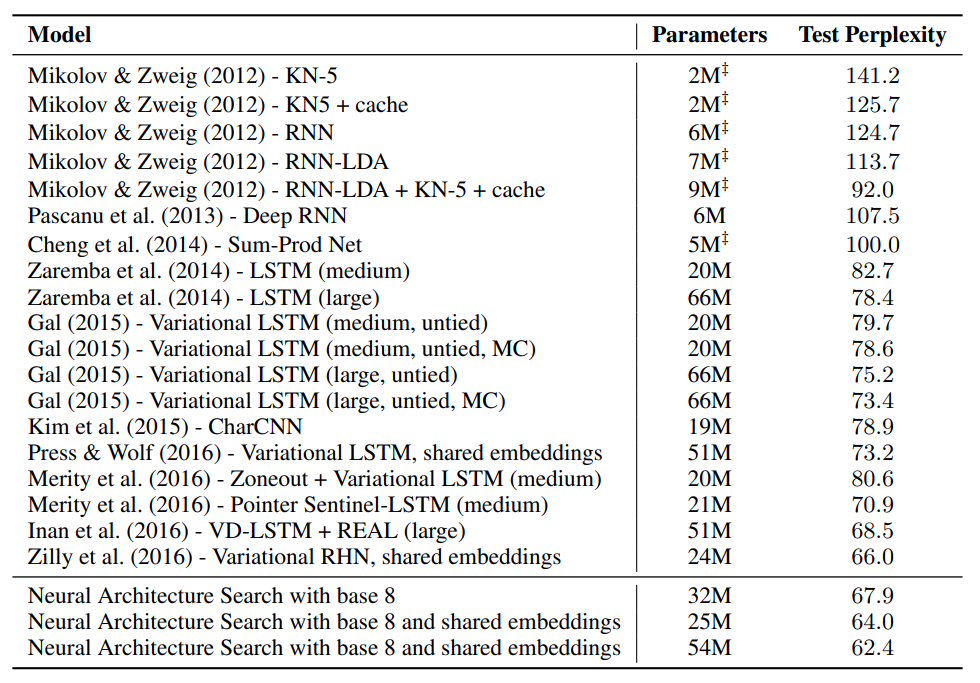
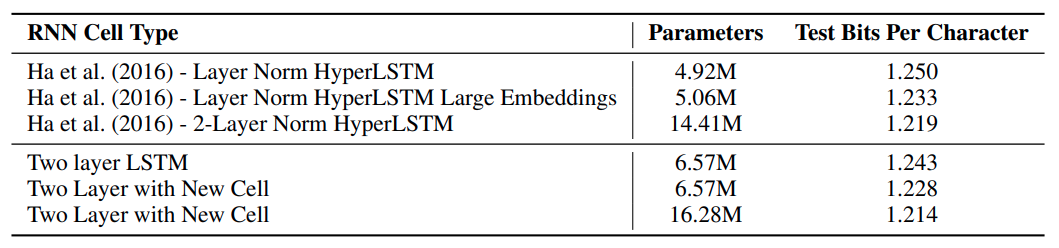
Table 2 : NASで探索したRNN(LSTM)3種類のPerplexity、パラメタ数
(二重短剣符はMerity et al., 2016)による推定値)
解説
言語モデリング(単語レベル)の評価指標にはPerplexityを用いる。
Perplexityは「正しい単語が選ばれる確率の逆数」で、「選択しうる単語の分岐数」と考える事ができる。
Perplexityが小さい程、言語モデルの性能が良いと言える。
RNNにDropoutを適用する場合は、2層以上のRNNにおいて、次タイムステップへの隠れ状態$h$は決定的に伝搬させ、同一タイムステップ中での入出力を確率的にDropoutさせることで情報を失うことなくDropoutを適用し過学習を防ぐことができる。
Activationのidentityは恒等関数の意。
転移学習
- 上記の手法で得られたモデルを使って、PTBでのcharacter language modelingを行いました。
- パラメタ数は増えましたが、SOTAを更新しました(BPC=1.214)。比較をTable 3に記載します。
- また、Google's Neural Machine Translation(GNMT)のフレームワークを用いて、英独の機械翻訳を行いました。
- 既存のLSTMセルよりも、BLUEスコアが0.5改善しました。
解説
言語モデリングが単語レベルでモデル化をしているのに対して、character language modelingは文字レベルでモデル化を行う。
評価指標はBits Per Characterであり、小さいほどモデリングの性能が良い。
数理的には1文字あたりのエンコードに必要なBit数であり、クロスエントロピーとほぼ同義。(文献によるが、前者は底が$e$、後者は2の場合が多い)
機械翻訳の評価指標BLUE(BiLingual Evaluation Understudy)は大きいほど翻訳の性能が良い。
参考
Google's Neural Machine Translation(GNMT)解説
NLPの様々なMetric解説
単語レベルと文字レベルそれぞれのSOTAまとめ
Control Experiment 1 – Adding more functions in the search space
- ロバスト性を検証するため、Combinationの探索空間に$max$を、Activationの探索空間に$sin$を加えて同様の実験を行いました。
- 結果、探索空間が広くなっても、同程度のパフォーマンスのモデルを発見できる事がわかりました。
- Figure 8に、$max$と$sin$を探索空間に含めた場合のベストな構造を図示します。
解説
Combinationの$max$は、2入力の大きい方を出力する関数。
Control Experiment 2 – Comparison against Random Search
- 方策勾配法の代わりにランダムサーチ(RS)で探索した場合との比較を行いました。
- それぞれの手法(NAS, RS)の上位1,5,15位(までの平均)の手法のPerplexityの差をFigure 6にプロットしました。
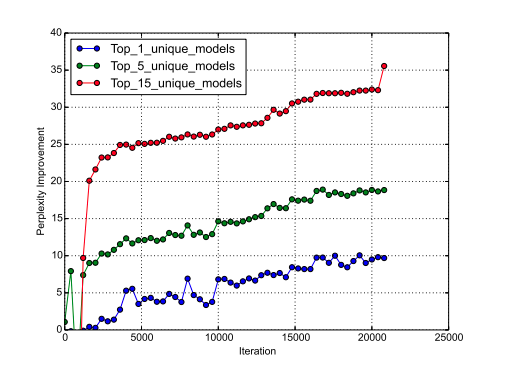
Figure 6 : NASで探索したモデルとRSで探索したモデルとのPerplexityの差
5. CONCLUSION
- 本論文のポイントは、ControllerにRNNを使ったため柔軟である(可変長の構造空間を探索できる)点です。
- CIFAR-10とかPTBの言語モデリングで良いパフォーマンスが出せました。
- 本手法で見つけたRNN(Child Networkの方)はNASCellという名前でTensorFrowに公開しました。
6. APPENDIX
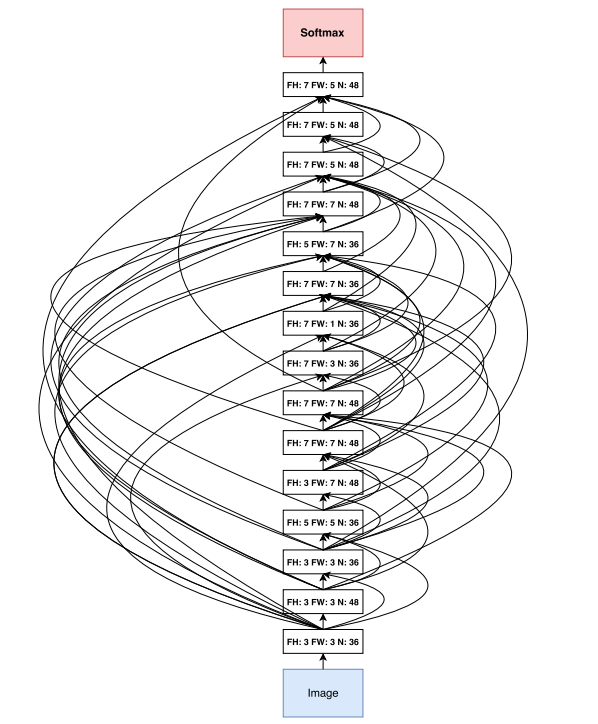
Figure 7 : セクション4.1で自動的に設計された15層DNN(CIFAR-10で精度94.5%)
解説
4種類の実験の内、v1条件(探索空間にストライド・プーリングを含まない)のモデル。
図中のFH, FW, Nはそれぞれフィルタ高さ、幅、フィルタ数。
Skip connectはConcatenateで結合される。
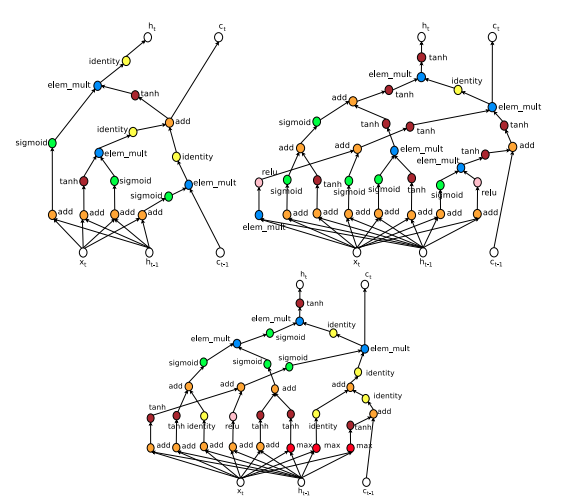
Figure 8 : NASで設計されたLSTM
左上 : LSTMの例
右上 : セクション4.2で自動的に設計されたLSTM
下 : Control Experiment 1で自動的に設計されたLSTM(探索空間に$max$と$sin$が含まれている)
解説
探索空間に$max$と$sin$を含めた場合も、$sin$は選ばれていない。
感想
強化学習で微分不可能な目的関数を最適化する+それをNN設計の自動化に応用するという点がとても面白かったです。
「Controllerの設計にハイパラが存在すること(Leaf node数とかプーリングレイヤの場所とか)」「探索空間にハイパラが存在すること(CNNのフィルターサイズをどの整数から選ぶかとか)」「計算量が高すぎること」「(Skip connectなど)既存の構造を表現することはできるが、ブレイクスルーとなる新しい要素(マクロな構造ではなく、ミクロな要素)を生むことは出来なさそうなこと」あたりが改善点だと思いました。
→ASNG-NAS(Akimoto et al., 2019)という手法がありました。
「Controllerにカテゴリ分布を使う」「自然勾配法を使う」などの工夫でハイパラ・計算量を削減しています。
(0.11GPUdayでCIFAR-10の分類のTest errorが2.89%。すごい)
co-authorのSaitoさん(Twitter)の解説スライドと合わせて読み込みたいと思います。