はじめに
2019年12月に刊行された「ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践」の第12章「交差検証によるバックテスト」について翻訳者が補足解説します。CPCV(Combinatorial Purged Cross-Validation)法について説明します。
色々なアイデアが詰まったこの本全体の中でも、CPCVは特に有用性が高い手法ではないかと思います。にもかかわらず本章の記述はとてもわかりにくいです（汗）。翻訳の際にはできるだけ原文に忠実に訳しましたが、実にわかりにくい。CPCVの比較対象となっているウォークフォワード（WF）法と交差検証（CV）法の定義がちゃんとされていないとか。謎の数式が多いとか。pythonコードがないとか。
ということで本記事は、サラッと読めてCPCV法がざっくり理解できるよう試みたいと思います。
WF（ウォークフォワード）バックテスト
機械学習を使った投資戦略のバックテストをする際に、ふつうに時間軸に沿って行うのがウォークフォワード(WF)法です。その時点より前のデータを使ってモデルを訓練して、その時点の投資判断をしていく、というのを時間を進めながら繰り返します。
次の表をごらんください。1月から6月の6ヶ月分のデータを使ってバックテストする場合を考えます。便宜的に、バックテストは1ヶ月単位で進めることとします。
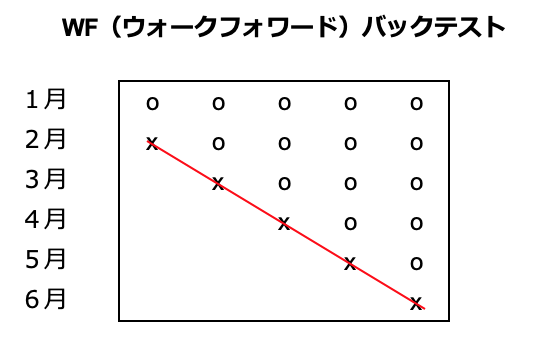
表の中で、"o"印は訓練データ、"x"印はテストデータを示しています。"x"の期間に実際に投資判断を行って、その結果（パフォーマンス）をつなげたものがこの投資期間のバックテスト結果となります。（赤線で示しています）
言葉で説明すると
・1月のデータでモデルを訓練して、2月に運用してパフォーマンスを計測
・1〜2月のデータでモデルを訓練して、3月に運用してパフォーマンスを計測
・1〜3月のデータでモデルを訓練して、4月に運用してパフォーマンスを計測
・1〜4月のデータでモデルを訓練して、5月に運用してパフォーマンスを計測
・1〜5月のデータでモデルを訓練して、6月に運用してパフォーマンスを計測
としてから、2月〜6月のパフォーマンスをつなげたものが、WFバックテストの結果となります。1月は書籍の12.2.1節でいう「ウォームアップ期間」になります。
バックテスト結果のシャープレシオがいくつ以上だったらOKなので実戦投入しようとか、複数の戦略をバックテストしてシャープレシオが一番高いものを選ぼう（これには後述する大きな問題がありますが）、とかいうふうに使います。
CV（交差検証）バックテスト
次はCV法です。CV法では時系列にこだわらず、未来のデータで訓練したモデルで過去の投資判断をしてもよいものとします。
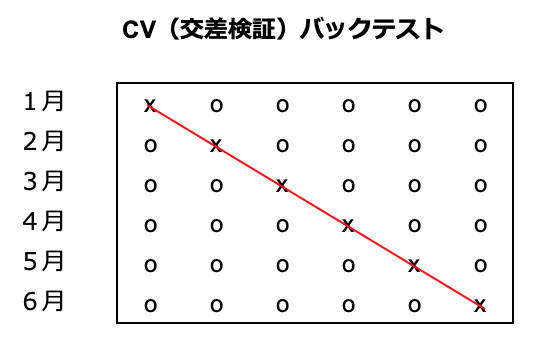
言葉で説明すると
・2〜6月のデータでモデルを訓練して、そのモデルで1月を運用しパフォーマンスを計測
・1、3〜6月のデータでモデルを訓練して、そのモデルで2月を運用しパフォーマンスを計測
（中略）
・1〜5月のデータでモデルを訓練して、そのモデルで6月を運用しパフォーマンスを計測
という具合です。
ウォームアップ期間が必要ないし、すべての投資判断が5ヶ月分のデータで訓練されたモデルでなされる、というのがWF法と比較した時の長所です。でも得られるバックテスト経路は変わらず一つです。
CPCV(Combinatorial Purged Cross-Validation、組合せパージング交差検証）バックテスト
さていよいよ本書が提案するCPCV法です。CV法を拡張して、テストデータ期間を1つでなく2つ（以上）にして、その組合せを生成することにより経路を増やす手法です。
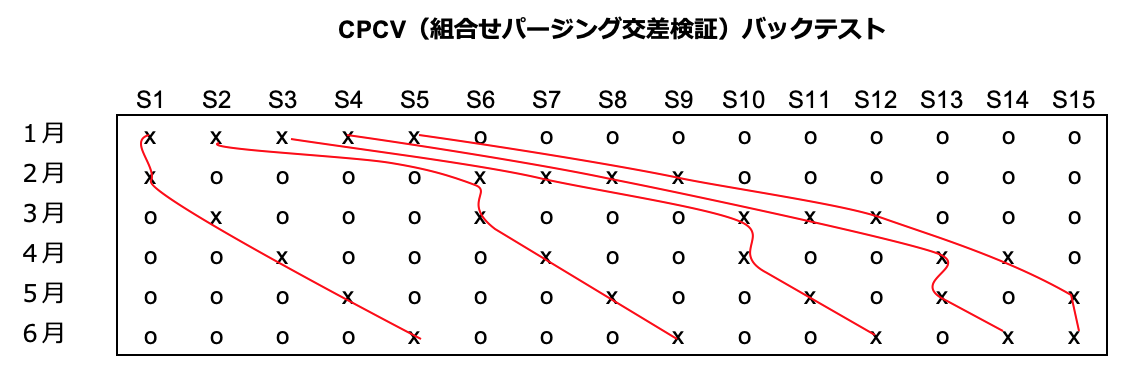
先ほどの図のCV法と比較すると、テストデータ（"x"印）が1つから2つになっています。これにより、訓練データとテストデータの組合せを $_{6} C _{2}=15$ 通り作ることができ、これをつなげて赤線で示した $\varphi[6,2]=5$ 通りのバックテスト経路を作ることができます。
お気づきかと思いますが上記の図は、書籍p212の図12-1, 図12-2と同じものです。（書籍では"o"が空白になっている）
Purging(パージング)とEmbargo(エンバーゴ)
もう一つ、CPCVの重要なポイントが、パージングとエンバーゴという処理を入れていることです。パージングとエンバーゴは第7章で出てきた手法で、時系列データのクロスバリデーションにおいてリーケージの原因となるようなデータを訓練データから落とす前処理です。ここでは概念図を再掲しておきます。(Source: 原著者ホームページ)
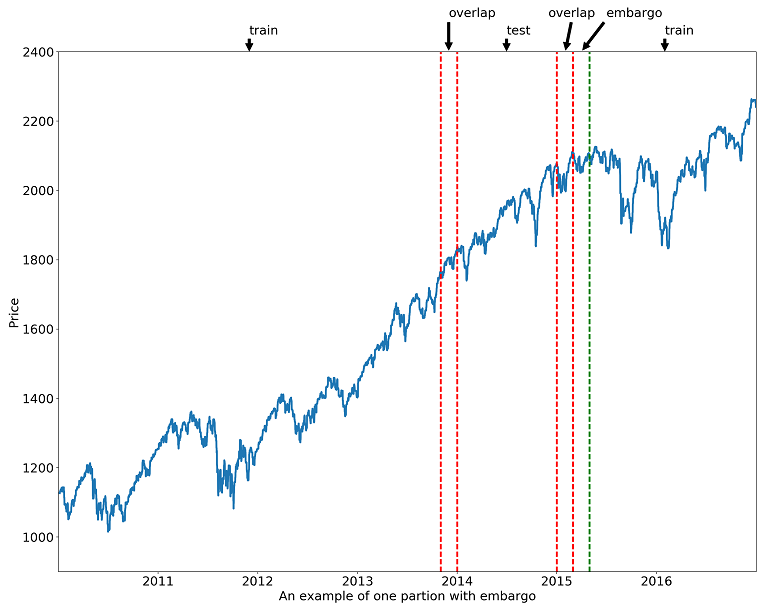
時系列データでCV（CPCVも含む）バックテストをする際には、パージングとエンバーゴを行わないと誤ったモデル選択をしてしまう可能性が高くなります。
CPCVは何がうれしいのか（12.5節）
本書でMarcosが繰り返し指摘するのがバックテストのオーバーフィット問題です。Bailey et al.[2014]をもとにしたこちらの記事の下記チャートは、Marcosが"the most important plot in finance"と呼んでいるものです（大げさだけど…）。
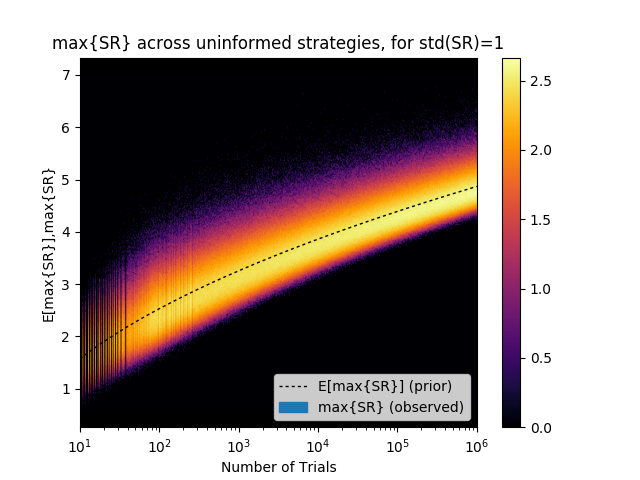
横軸はバックテスト試行回数、縦軸はバックテスト結果のシャープレシオの最大値（の分布、黒点線が期待値）です。つまり、真のシャープレシオがゼロの戦略でも、バックテスト試行回数を増やせば高いシャープレシオが得られてしまう。例えばグラフの横軸 $10^3$ のあたりを見ると、1000回試行すれば、3以上のSRを叩き出す戦略が平均して1つは見つかる、ということです。
この期待値 $E [max \{ y_i \} _{i=1,\cdots,I} ]$ は、試行回数$I$ が増えれば増えるほど、またバックテストのバリアンス（分散）$\sigma[y_i]$ が大きくなればなるほど高くなります。
WFバックテストでは、このバックテストのバリアンス $\sigma[y_i]$ が高い、つまりバックテストを試行するごとの結果のブレが大きい、というのが本書の指摘です。上で見たようにテスト期間の前半では少ない割合のデータで学習したモデルとなるため、その分結果が観測値のノイズに影響されやすいためです。
CVバックテストでは、各時点では同じ量のデータで学習したモデルを使うため、WFよりはバリアンスが小さくなります。しかしWFと同様に、バックテストの結果得られるのは一つの経路で計算された一つのシャープレシオのみです。
CPCVでは、WFやCVのように一つのシャープレシオではなく、複数（上記の例では5つ）のシャープレシオの分布が得られます。これによって、得られる結果の分散が小さくなる、つまりオーバーフィットの危険性を低減することができるというわけです。
参考〜Pythonライブラリ・動画解説
CPCVはmlfinlabパッケージで実装されています。pip install mlfinlab して CombinatorialPurgedKFold.split(X,y)で訓練／テスト分割を出力してくれます。
（追記）残念ながらmlfinlabパッケージは有料化されてしまいました。
別の実装
https://github.com/sam31415/timeseriescv
解説記事
https://blog.quantinsti.com/cross-validation-embargo-purging-combinatorial/
動画解説
https://quantoisseur.com/2019/11/05/combinatorial-purged-cross-validation-explained/
