1. 背景
世間からはだいぶ遅れているのかもしれませんが、将来何かの役に立つかも知れないと思い、最近機械学習の勉強をしています。特に、この分野ではとても有名(らしい)、PRML(Pattern Recognition and Machine Learning)という本を読んで勉強しています。今は、4章の「線形識別モデル」を読んでいるのですが、「線形分離可能なデータに対しては、必ず過学習が発生してしまう」(「4.3.2 ロジスティック回帰」(P205))という記述がよくイメージできなかったので、実際にデータを作って分析してみることで理解を深めようと思い、色々と試してみました。
ちょうどクリスマスのAdvent Calendarのシーズンでしたので、せっかくなので結果を投稿してみることにしました。同じような疑問を持たれている方のお役に立てれば嬉しいです。
2. ロジスティック回帰の概要
まずは、簡単にロジスティック回帰の概要を説明したいと思います。(本題ではないので、さらっと流します。詳細は、PRMLや、他の機械学習の教科書をご参照ください。)
2.1 線形識別モデル
線形識別モデルは、簡単に言うと、あるベクトル$\mathbf{x}$が与えられた時に、$\mathbf{x}$がどのクラスに分類されるかを判別するものです。
一般的に、入力のベクトルは$\mathbf{x}$は$n$次元、分類するクラスは$k$個のものを考えることができますが、今回は、簡単のため、1次元の入力ベクトル$\mathbf{x}$を2つのクラスへ分類することを考えます。
2.2 ロジスティック回帰
ロジスティック回帰は、線形識別モデルの1つです(「回帰」という名前ですが、実際には「分類」をするためのモデルだそうです)。具体的には、ロジスティック回帰では、入力ベクトル$\mathbf{x}$を以下の方法で分類します。
- 入力ベクトル$\mathbf{x}$に重みベクトル$\mathbf{w}$をかけ、「決定面」$\mathbf{w}^{t} \mathbf{x}$を求める。
- 1で求めた決定面をシグモイド関数に入力し、$\mathbf{x}$が各クラスに含まれる確率を求める。(シグモイド関数は、$(-\infty, +\infty) \rightarrow (0, 1)$にマッピングする関数なので、$\mathbf{w}^{t} \mathbf{x}$を確率密度に変換することができます。)
- $\mathbf{x}$は、2で求めた確率がもっとも大きなクラスに属すると分類する。(2クラスの分類の場合は、クラス1の確率が0.5以上の場合はクラス1に分類されるものとする。)
3. ロジスティック回帰の過学習について調べる
では本題です。先ほども少し書きましたが、PRMLによると、「線形分離なデータに対しては、ロジスティック回帰は必ず過学習を起こしてしまうのだそうです。具体的には、
- 線形分離可能なクラスについては、$\mathbf{w} \rightarrow +\infty$が最尤解となる。
- そのそき、すべてのデータについて、事後確率$P(C_{k}|\mathbf{x})=1$となってしまう。
とのことです。一方で、PRMLのその次の節には「誤差関数はパラメータベクトル$\mathbf{w}$の凸関数なので、必ず唯一の最小解を持つ」ともあります。私は最初上記意味がよく分からなかったのですが、よく考えると以下のような意味なんじゃないかと理解しました。
- とにかく誤差関数は凸関数となる。
- しかし、$\mathbf{x}$が線形分離可能な場合は、$+\infty$が最小になるような凸関数になっている(反比例のグラフみたいなイメージ)。
ということで、$x$が1次元のときに、実際に、線形分離可能なデータと、線形分離できないデータについて、決定面や尤度関数や誤差関数を求めてみることで、上記理解が正しいかを試してみました。
3.1 データの作成
以下2パターンのデータを作成しました。
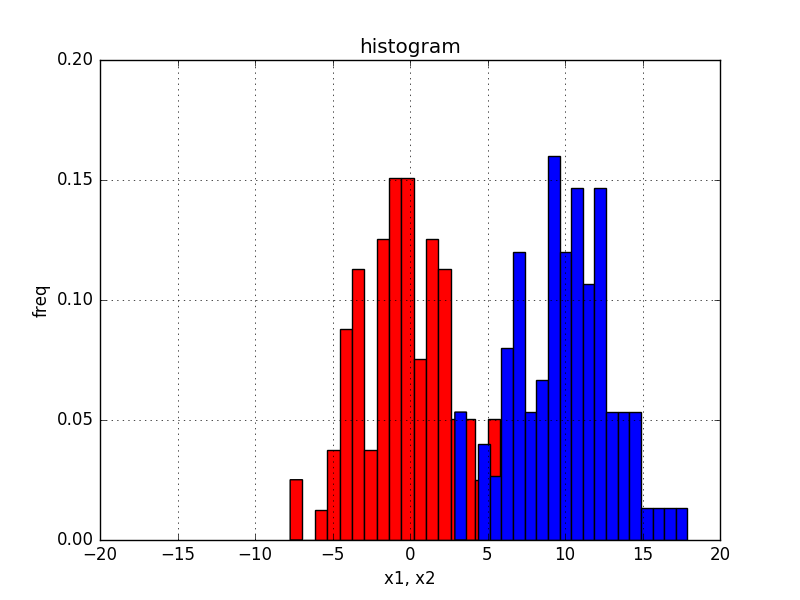
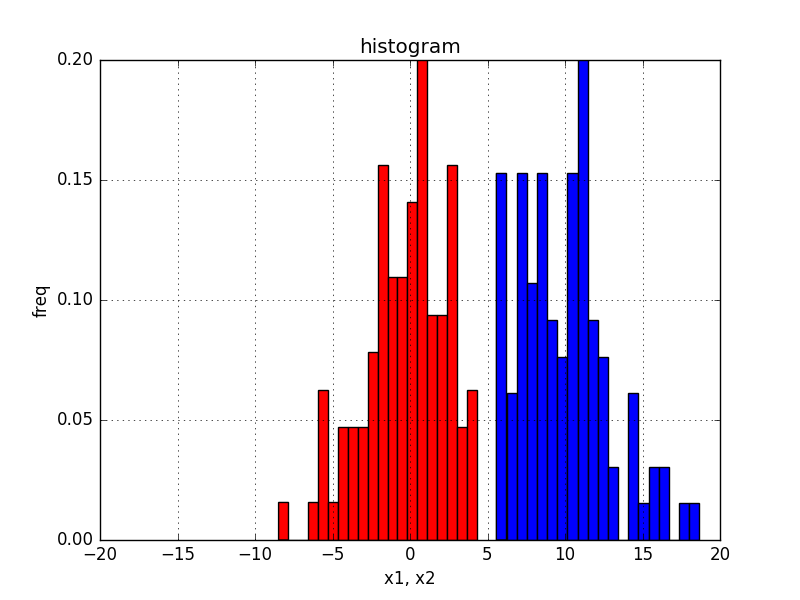
- 線形分離不可能なデータセット
- クラス1: 平均$0$、分散$3$の正規分布に従うデータ
- クラス2: 平均$10$、分散$3$の正規分布に従うデータ
- 線形分離可能なデータセット
- 上記1のデータセットを加工し、x=5で分離でできるようにしたデータ
上記データセットは、それぞれ、以下の通り作成しました。
num_samples = 100
mu1 = 0
sigma1 = 3
mu2 = 10
sigma2 = 3
x1 = sigma1 * np.random.randn(num_samples) + mu1
x2 = sigma2 * np.random.randn(num_samples) + mu2
# データセット1に対して、以下処理で加工
thr = 5
x1[x1>thr-0.5] = x1[x1>thr-0.5]-thr
x2[x2<thr+0.5] = x2[x2 < thr+0.5]+thr
ここで、注意ですが、今回の入力データ$x$は1次元ですが、通常は「バイアス成分」を考えるため、$\mathbf{w}$は2次元になります。つまり、決定面は$\mathbf{w}^{t} \mathbf{x} = w_{1} x + w_{0}$となります。
上記方法に作成したデータセットを散布図で表示してみると、以下のようになります。データセット2は、$x=5$でスパッと分離できていますね。
ヒストグラムで表すと以下のようになります。
3.2 wを動かし、決定面、事後確率、対数誤差がどうなるか調べてみる。
次に、$\mathbf{w} = (w_{0}, w_{1})$を動かしてみて、決定面・事後確率・対数誤差がそれぞれどのように変化するかを見てみることにします。$w_{0}$と$w_{1}$はそれぞれ独立に動かしてみてもよいのですが、今回は、決定面が$x=5$を通るように動かしてみることにします。(つまり、$\mathbf{w}$は、$w_{1} = - w_{0} / 5$を満たすように動かすことにする。)
では、まずは、早速結果を見てみましょう。(後ほど図の見方の説明をします。)
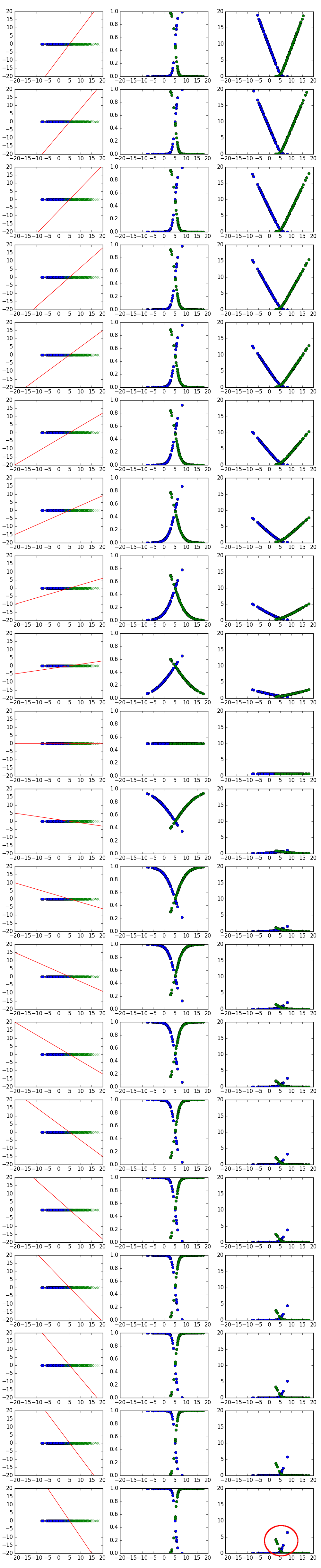
3.2.1 データセット1(線形分離不可能な場合)
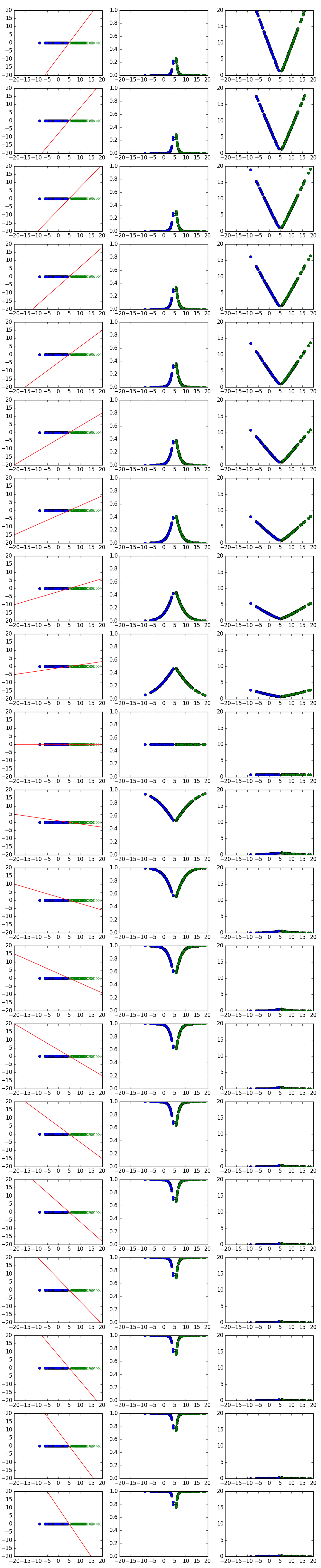
3.2.2 データセット2(線形分離可能な場合)
3.2.3 図の説明
先ほども少しご説明したように、図は、データセット1とデータセット2について、それぞれ、$w_{1} = - w_{0} / 5$を満たすように$w_{0}$、$w_{1}$を動かした時に、決定面・事後確率・対数誤差がそれぞれどうなるかを調べたものです。詳細は以下のとおりです。
- $w_{0}$を$-10$から$10$まで動かす。(対応して、$w_{1}$は$2$から$-2$まで動く)
- つまり、決定面$\mathbf{w}^{t}\mathbf{x} = w_{1}x + w_{0}$は、常に$x=5, \mathbf{w}^{t}\mathbf{x}=0$を通るように$\mathbf{w}$を動かしている。
- 各行の図が、1つの$w_{0}, w_{1}$の値に対応。また、各行について、3つの図は左からそれぞれ、決定面、事後確率、対数誤差を表す。それぞれの図の詳細は以下のとおり。
3.2.3.1 決定面の図
各行の左の図は、横軸が$x$、縦軸が$\mathbf{w}^{t}\mathbf{x}$を表したグラフです。赤い直線は$\mathbf{w}^{t}\mathbf{x} = w_{1}x + w_{0}$を表しています。
- 式からも分かるように、$w_{0}$は決定面の切片、$w_{1}$は決定面の傾きを表す。
- グラフは常に$(5,0)$を通る。(そのように$w_{0}, w_{1}$を動かしているので。)
- $x$軸上に、データの散布図をあわせて表示している。
3.2.3.2 事後確率の図
各行の真ん中の図は、事後確率を表した図となります。つまり、横軸が$x$、縦軸が事後確率$P(C_{k}|x)$です。事後確率はシグモイド関数なので、$(0,1)$上のS時のグラフになっていることが分かります。詳しい考察は後ほどご説明します。
3.2.3.3 対数誤差の図
各行の右の図は、対数誤差のグラフです。実際には、正確に言うと、対数誤差の各要素を表しています。つまり、このグラフの各点の合計が対数誤差となります。対数誤差$=-log(事後確率の対数)$ですので、このグラフの動きは、事後確率の動きと上下が反転した動きとなっています(事後確率が↑のとき対数誤差は↓)。
3.2.4 考察
ロジスティック回帰の目的は、対数誤差関数を最小にすることですので、一番右の各点の合計が最小になる$\mathbf{w}$が最適な$\mathbf{w}$ということになります。では、データセット1、2それぞれについて、$\mathbf{w}$を動かすと対数誤差関数はどのように変化して行っているかを考察してみることにします。順番が逆ですが、まずはデータセット2から見てみることにします。
3.2.4.1 線形分離可能なデータ(データセット2)の考察
下のほうの図に行くにつれて(=$w_{0}$が大きくなるにつれて)、右の図の各点は$0$に張り付いて行っていることが分かります。また、この時、$w_{0}$はどんどん大きくなり、$w_{1}$はどんどん小さくなって行っています。つまり、$|\mathbf{w}|$をどんどん大きくしていくと、それにつれて決定面の傾きはどんどん急になり、かつ、対数誤差関数(=右図の各点の合計)は限りなく$0$に近づいていくことが分かります。また、真ん中の事後確率の図から、ほとんどの点$x$について、事後確率が$1$に張り付いていることも確認できます。
3.2.4.2 線形分離不可能なデータ(データセット1)の考察
次に、データセット1の結果を見てみます。この場合もデータセット2の場合と同様に、下のほうの図に行くにつれて(=$w_{0}$が大きくなるにつれて)、右の図の各点は$0$に張り付いて行っていますが、一部、$x=5$付近のデータは逆に下のほうの図では大きくなってしまっていることが分かります(図の赤丸付近)。このため、データセット1については、$w_{0}$をどんどん大きくしていっても、減少していく箇所と増加していく箇所のトレードオフにより、必ずしも対数誤差関数は小さくなっていかないことが分かります。(パッとみた感じでは、上から11番目くらいのグラフが対数誤差(一番右の図の各点の合計)は一番小さくなっている感じでしょうか。)
3.2.4.3 線形分離不可能な場合(データセット1)と分離可能な場合(データセット2)の違い
上記見てきたように、対数誤差関数のグラフは、データセット1、データセット2ともに、一番下のグラフ($w_{0}$が大きい時)では、青色のグラフ(クラス1に属する点)は$x \lt 5$で$0$に張り付いており、緑色のグラフ(クラス2に属する点)は$x\gt5$で$0$に張り付いていることが分かります。
線形分離可能な場合(データセット2)では、(線形分離できているので)、クラス1の点は必ず$x\lt5$にのみ存在し、クラス2の点は必ず$x \gt 5$にのみ存在するため、結果として、クラス1のグラフもクラス2のグラフも全て$0$に張り付いているのですね。
一方で、線形分離が不可能な場合(データセット1)では、クラス1、クラス2に属する点は双方ともに$x=5$の両側に存在することになります。このため$x=5$の反対側に存在する点についてはグラフが$0$に張り付かないということが起こるということになるんですね。
3.3 wを動かした場合の対数誤差の動きをみてみる
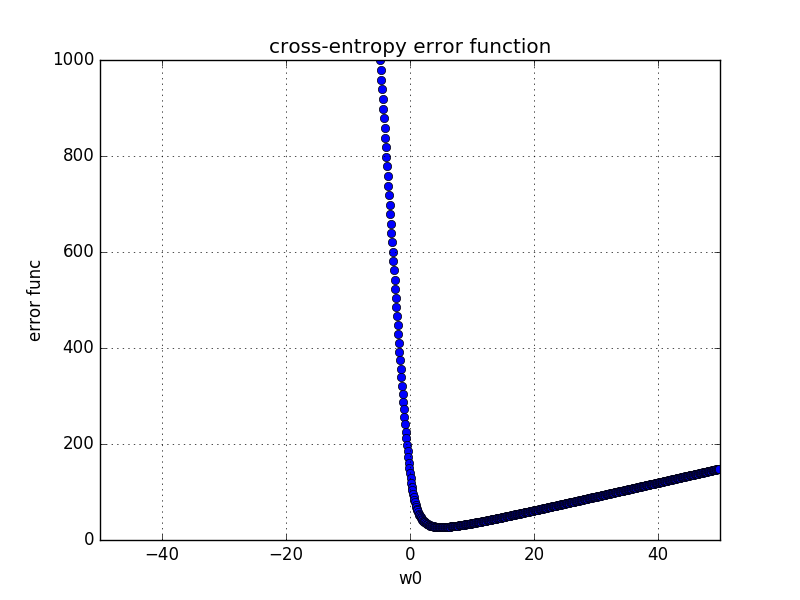
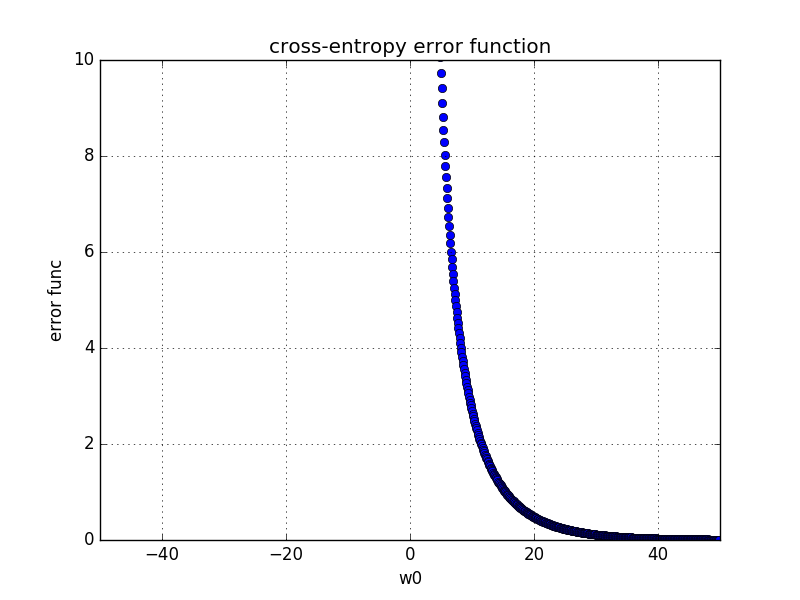
以上で、線形分離可能な場合は$|\mathbf{w}|$を大きくすると対数誤差はどんどん小さくすることができる一方で、線形分離不可能な場合は必ずしもそうではないということが想像はできました。では、次に、実際に、$\mathbf{w}$を動かした時に、出来上がりの対数誤差がどうなるかを見てみましょう。
- 線形分離不可能な場合
- 線形分離可能な場合
ん〜、確かに、冒頭の予想通り、線形分離可能な場合は凸関数ですが$\mathbf{w}$が大きくなるにつれてどんどん小さくなる関数になっていますね!
一方で、線形分離不可能な場合は、有限な最適解が存在していることが分かります。
4. 過学習との関係
で、次に私が湧いた疑問は、「$\mathbf{w}\rightarrow \infty$、事後確率$P(C_{k}|x)=1$」のときはなぜ過学習と言えるのか?ということです。これは次のような説明になると思います。今回のデータセット2の例では、$x=5$を境に、$x\lt5$では$P(C_{1}|x)=1$、$x\gt5$では$P(C_{1}|x)=0$となります。つまり、今回学習に用いたデータセットから導かれた結果では、$x\lt5$の点は必ずクラス1に属し、$x\gt5$の点は必ずクラス2に属するということです。しかし、これはたまたま今回のデータセットの境界が$x=5$であっただけであって、本当の境界は$x=4.5$かもしれません。その場合は、例えば、$x=4.7$の入力値に対しては、クラス2に分類されるのが本当は正しいのですが、今回の学習結果を用いると$x=4.7$の点はクラス1に分類されてしまうのです。つまり、今回の学習データにフィットしすぎている(=過学習)ということです。
5. ソースコード
ソースコードと言うほど大したものではないですが、一応GitHubにソース(jupyterのnotebook)をあげておきましたので、よろしければそちらも見ていただけましたらと思います(こちら)。
6. まとめ
個人的には、今回の分析をしてみてとてもすっきりしましたが、いざ書いてみると分かりにくくなってしまったかもしれません。疑問点や誤り等ありましたらコメントをいただけましたらと思います。また、PRMLを輪読等で一緒に勉強していただける方も募集中です(一人で読んでいると計算に詰まったりして時間がかかるので)。もしくは、おすすめの勉強会とかあっらご紹介していただけると嬉しいです。