本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
前回、ランクのご説明をしましたが、「大学で習うランクの計算方法とどのような関連があるのか?」というご質問を受けましたので、今回は、ランクの説明の補足として、ランクを手で計算する方法のご説明と、前回ご説明した「ランク=変換後の次元数」との関係をご説明したいと思います。
1. ランクを手計算する必要があるか?
まず始めにお伝えしておきますと、たぶん、行列式や逆行列の手計算も同様ですが、**大学1年生の授業以外では、ランクを手で計算する機会は99.9%無いのではないかと思います。**ただ、よく思い出してみると、私も大学1年生の時に、意味がわからないままこれらの計算をしていたことが線形代数でつまずいた原因の一つだったような気もしてきたので、前回ご説明した、ランクの意味とランクの手計算方法の関係をはっきりさせておいたほうがいいかなと思い、ちょっと説明を書いてみることにしました。
2. ランクの計算方法
説明すると言いつつ丸投げですみませんが、例えばこちらのサイト等(※)に説明があります。
(※)私はこのサイトとは全く関係無い者ですが、Googleで一番上に出てきたので。。
超ざっくりと言うと、要は、各行に、他の行を何倍かしたものを足し引きして、最終的にすべて0でない列の数がランクになるというイメージになります。大学1年の時に、とても退屈な思いをして勉強した「掃き出し法」による式変形ってやつですね。
3. 行列のランクの意味(おさらい)
次に、ランクの意味をさらっとおさらいしておきますと、
- ある行列$A$のランクとは、$A$により変換される変換先の空間の次元数
- 具体的には、行列$A=(\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n)$のランクは、角列ベクトル$\mathbf{a}_i$で張られる空間の次元数になる。
ということになります。詳細は第9回をご参照ください。
4. ランクの計算方法(上記2)とランクの意味(上記3)の関係
では、今回の本題ですが、ランクの計算方法とランクの意味の関係について見ていきます。
4.1. 掃き出し法の意味
まず、掃き出し法が何をやっているかの意味を考えてみます。以下の行列の2行目に1行目の-2をかける例を見てみましょう。
$$
\left(
\begin{matrix}
1 & 4 & 7 \
2 & 5 & 8 \
3 & 6 & 9 \
\end{matrix}
\right)
$$
実は、この掃き出しは、行列の掛け算で表現でき、左から以下のような行列を掛けているということなのです!(下の式の右辺をよーく眺めてみてください。)
$$
\left(
\begin{matrix}
1 & 0 & 0 \
-2 & 1 & 0 \
0 & 0 & 1 \
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 4 & 7 \
2 & 5 & 8 \
3 & 6 & 9 \
\end{matrix}
\right)=
\left(
\begin{matrix}
1 & 4 & 7 \
2+ (-2) \times 1 & 5 + (-2) \times 4 & 8+ (-2) \times 7 \
3 & 6 & 9 \
\end{matrix}
\right)
$$
くどいようですが、同様に、3行目に1行目の-3をかける操作は、行列の積を用いて以下のように表すことができます。
$$
\left(
\begin{matrix}
1 & 0 & 0 \
0 & 1 & 0 \
-3 & 0 & 1 \
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 4 & 7 \
2 & 5 & 8 \
3 & 6 & 9 \
\end{matrix}
\right)=
\left(
\begin{matrix}
1 & 4 & 7 \
2 & 5 & 8 \
3+ (-3) \times 1 & 6 + (-3) \times 4 & 9 + (-3) \times 7
\end{matrix}
\right)
$$
このように、ある行に、別の行の何倍かをかけるという操作は、単位行列の形を少し変えた行列(上記例のように、かける元とかける先に対応した成分に値を入れた行列)で表すことができるのです。
ちなみに、同様に、ある列に別の列の定数倍をかける操作は、右から行列をかける操作で表すことができます。
4.2. ある行列に正則な行列を掛けた時のランク(※)
(※)ご説明していなかったかも知れませんが、フルランクな正方行列(行数=列数の行列)のことを正則行列と言います。
次に、ある行列に、正則な行列を掛けた行列のランクは、元の行列のランクと等しいという性質があります。つまり、ある行列$X$と正則な行列$A$について、以下が成り立ちます。
$$
rank(AX)=rank(X)
$$
証明は省略しますが、前回のご説明のとおり、フルランクな行列は、例えば、2次元から2次元、3次元から3次元のように、次元を変えない変換を表していたので、まあ、イメージはわくのではないかと思います。
例えば、$3 \times 2$で、ランクが2の行列$X$があった時、これに、$3 \times 3$のフルランクな行列$A$を掛けた時に、$AX$のランクは、元の行列$X$のランクと同じで2になるということです。これは、
- まず、$X$により2次の空間全体が、3次元空間中の2次元の平面に変換される。
- 次に、この3次元の空間が$A$により3次元に変換される。よって、この3次元空間中の2次元の平面(1の平面)も2次元の平面に変換される。
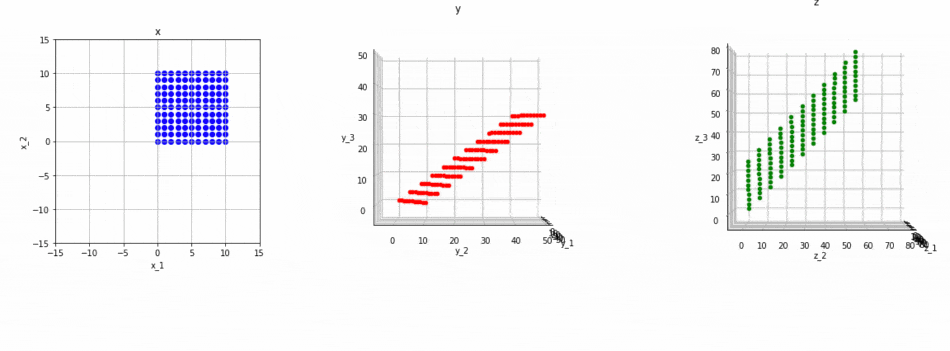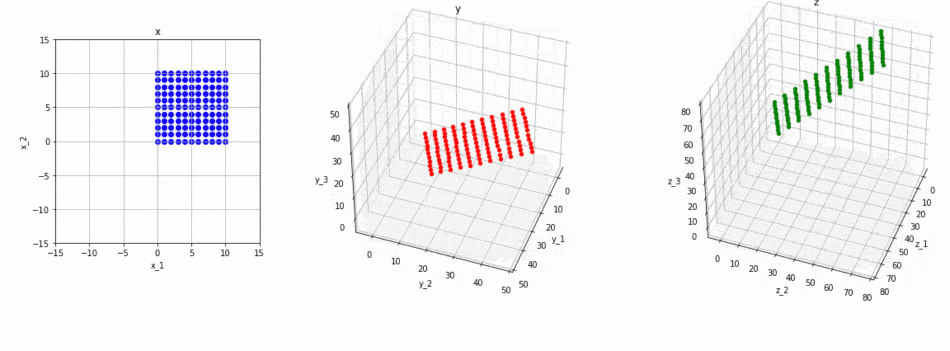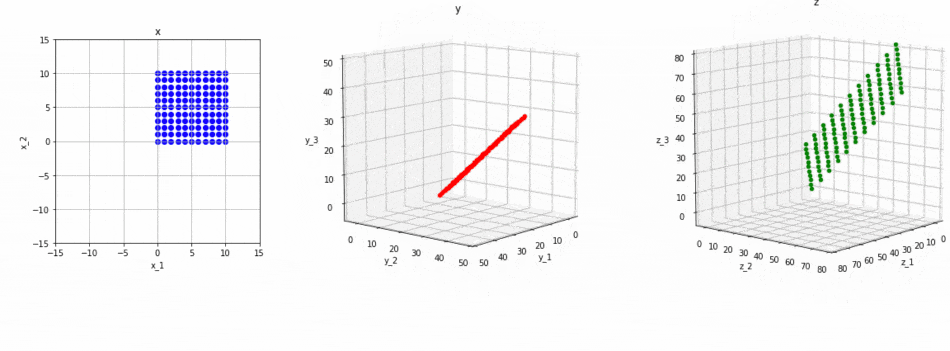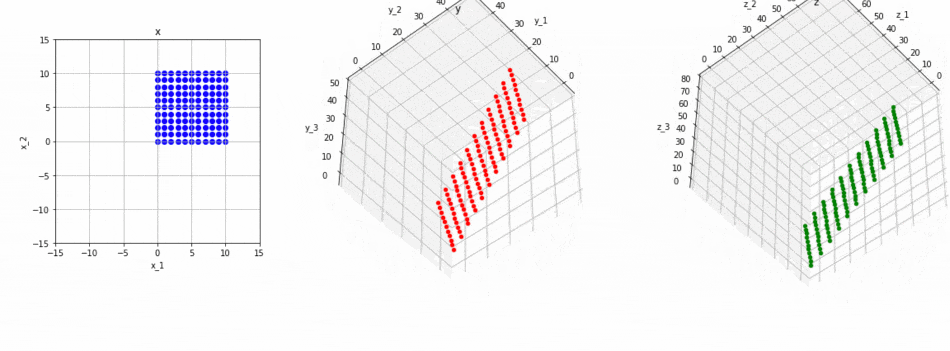
ということになります。イメージは以下の図のとおりです。
図の意味は以下の通りです:
- まず、$2 \times 3$の行列で、左図の2次元空間上の青色の平面が、中央図に3次元空間上の赤色の平面(2次元)に変換されます。
- 次に、フルランクの$3 \times 3$の行列により、中央図の3次元の空間が、右図の3次元の空間に変換されます。これに伴い、中央図上にあった赤色の平面(3次元中の平面)が、右図にある緑色の平面(3次元中の平面)に変換されます。
- 結果として、もともと2次元だった空間(左図の青色の部分)は、(3次元空間中の)2次元の空間(右図の緑色の部分)に変換されます。よってこの変換のランクは2であることが分かります。なぜならば、変換先が平面(=2次元)だからです。
ちなみに、証明は例えばこちら等にあります。(このサイトも私とは一切関係無いですですが、リンクを張らせていただきました。)
4.3. 掃き出し法で使われる行列は正則
次に、掃き出し法で使われる行列は正則になることを見てみましょう。4.1で見てきたように、掃き出し法で使われる行列は、例えば、以下のような形をしています。
$$
\left(
\begin{matrix}
1 & 0 & 0 \
0 & 1 & 0 \
4 & 0 & 1
\end{matrix}
\right)
$$
この例は、3行目に、1行目の4倍を足すという操作を表す行列でした。この行列は、よく見ると、単位行列の$(3,1)$の成分だけを$4$に置き換えている形になっています。これは、$x$軸方向の成分を、$z$方向に4倍だけシフトさせる変換を表していることが分かります。(詳しくは第6回の「1. 行列の各列の意味」をご参照ください)。よって、この行列による変換先は、$x$軸の方向が4だけシフトだけなので、(変換先が潰れていないので)正則になります。つまり、掃き出し法で使われる行列は正則になると言えます。分かりにくいかも知れないので、次の$2 \times 2$の行列でもう少し詳しく確認してみましょう。
$$
\left(
\begin{matrix}
1 & 0 \
2 & 1
\end{matrix}
\right)
$$
正規直交基底$\mathbf{e}_1=(1,0)^t, \mathbf{e}_2=(0,1)^t$の、この行列による変換先$\mathbf{a}_1, \mathbf{a}_2$は、以下のようになります。
$$
\mathbf{a}_1 =
\left(
\begin{matrix}
1 \
2
\end{matrix}
\right)
, \mathbf{a}_2 =
\left(
\begin{matrix}
0 \
1
\end{matrix}
\right)
$$
この基底を図示してみると以下のようになります。$y$軸方向の軸が$x$方向に2だけ平行移動された平行四辺形になっていますね。なので、(変換先が潰れていないので)、この行列は2次元から2次元への変換。つまり、ランク=2、フルランクであることが分かります。
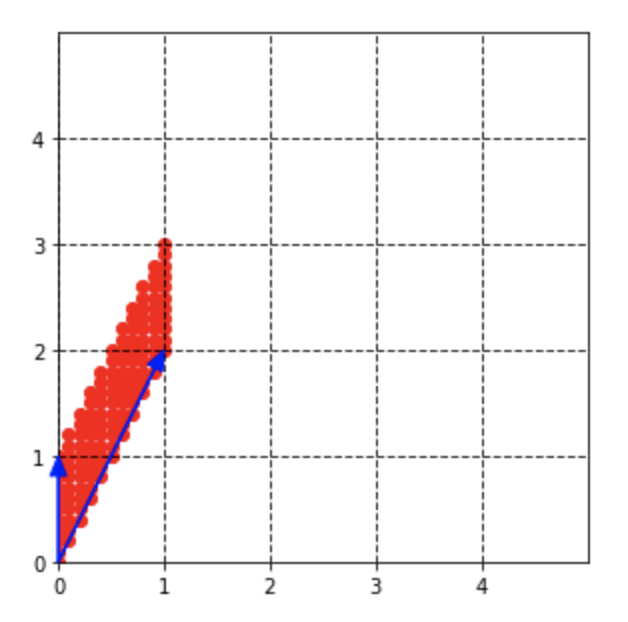
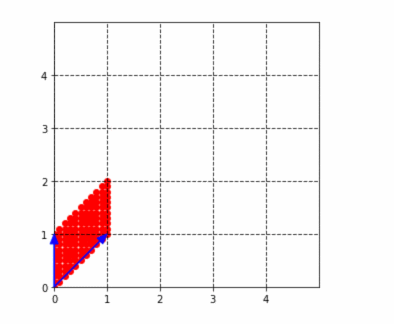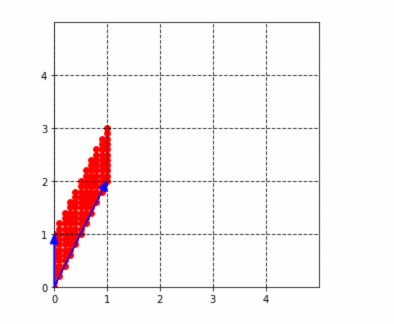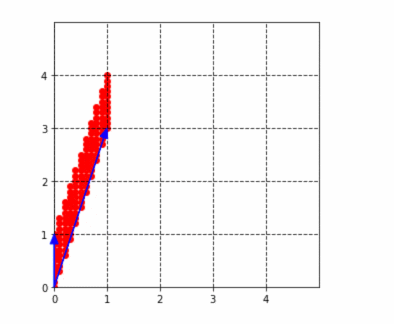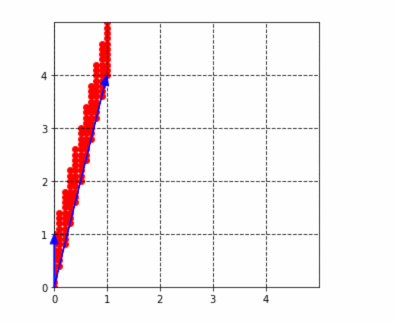
ここで、(2,1)の成分は、どんな整数が入っていても、この結果は必ず平行四辺形になります。なぜなら、この行列のすべての対角成分が1になっているからです。試しに、以下の行列で、$a$を1〜4まで動かしてみると、下図のようになります。確かに平行四辺形はだんだん細長くなっていきますが、潰れることはないですね!(なぜなら高さ(x軸)が必ず1だからです。)
$$
\left(
\begin{matrix}
1 & 0 \
a & 1
\end{matrix}
\right)
$$
また、ここでは、図示した時に見やすいよう、$2 \times 2$の行列で考えましたが、一般的に$n$次元でも同様のことが成り立ちます。(少しイメージしていただくと、3次元でも同様であることはお分かりいただけると思います。)
4.4. 結論:掃き出し法による操作の前後ではランクは不変
ここまでで、
- 掃き出し法の操作は、対象の行列に正則行列をかけるという形で表すことができる。→4.1, 4.3
- 正則行列をかける前後では、対象の行列のランクは不変 →4.2
ということが分かりました。つまり、掃き出し法の操作の前後ではランクは不変ということになります。ですので、掃き出し法によるランクの計算方法は、正則な行列を順々に掛けていくことによりもともと求めたい行列のランクを変えずに行列を分かりやすい形に変形していき、最後に行き着いた行列のランクを調べることで、元々求めたい行列のランクを求めているということが分かりました。
5. まとめ
今回は、掃き出し法によるランクの計算の意味について見てみました。この記事により、退屈な掃き出し法についての理解を深めていただける方がいらっしゃると嬉しいです。(ただ、最初の話と繰り返しになりますが、大学1年生の線形代数以降で掃き出し法を使う機会は無いかも知れませんが。。。)
次回はさらっと逆行列についてご説明をする予定です。