本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
たまに思い出したようにの更新ですみませんが、今回は行列のランクについてご説明をしたいと思います。
1. 行列の各列の意味(復習)
まず、行列のランクを理解するためには、行列の各列の意味について理解をすることがとても重要になります。第6回の冒頭でご説明しました通り、行列$A$の各列は、変換元の空間の正規直交基底の変換先のベクトルを表しています。
例えば、
$$
A=(\mathbf{a}_1, \mathbf{a}_2)=
\left(
\begin{matrix}
2 & 1 \
1 & 4
\end{matrix}
\right)
$$
の1列目$\mathbf{a}_1=(2, 1)^t$は、変換元の正規直交基底$\mathbf{e}_1=(1, 0)^t$に$A$を掛けた時の変換先を表しています。これは、実際に、$A \mathbf{e}_1$を計算してみると確認することができます。
つまり、基底$\mathbf{e}_1=(1,0)^t$, $\mathbf{e}_2=(0,1)^t$で表される空間は、行列$A=(\mathbf{a}_1, \mathbf{a}_2$)の各列によって$\mathbf{a}_1=(2,1)^t$, $\mathbf{a}_2=(1,4)^t$で表される空間に変換されることになります。詳細は第6回をご参照下さい。
2. 行列のランク
では次に、今日の主題である、行列のランクのご説明です。**行列$A$のランクは、行列$A$による変換先の空間の次元数として定義されます。例えば、上記の例ですと、ランクは2です。この例は2x2の行列(2次元から2次元への変換)なので、変換先の次元は2なのは当たり前ではないか!と思われるかも知れませんが、実は、必ずしも行列の次元とランクは一致はしない**のです!以下で、行列の次元とランクが異なる例を見て見てみましょう。
2.1. 2x2行列で、ランクが2の場合
まず、先ほどあげた例で、元の空間上の点を(0,0)〜(10,10)に変化させた時に、変換先の点がどのようになるかを見てみましょう。
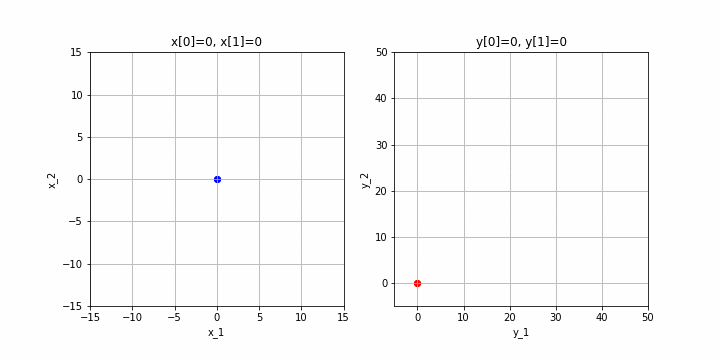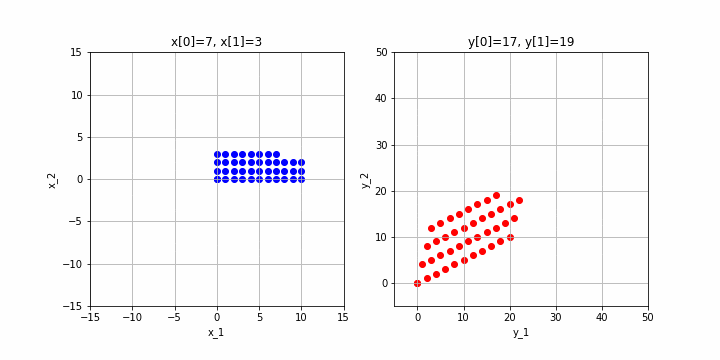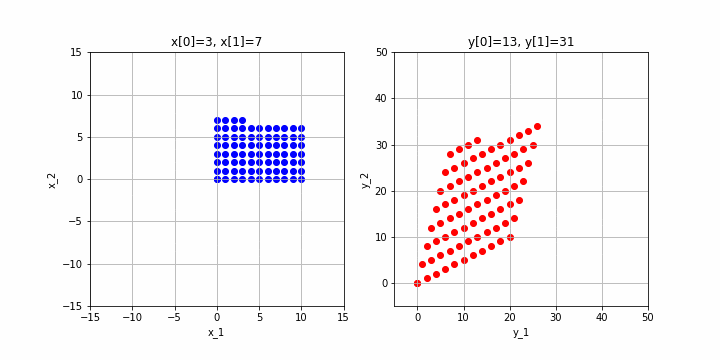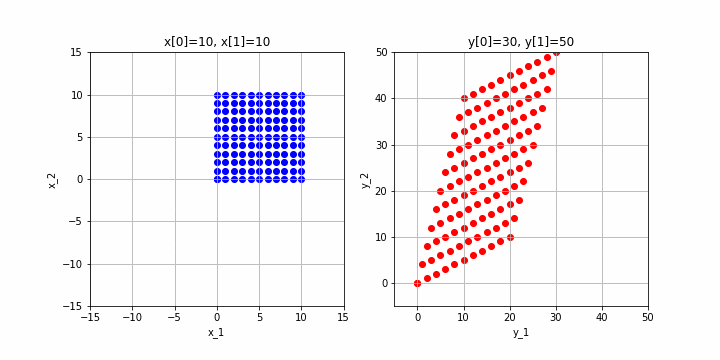
※クリックすると動画になるはずです。
左が元の空間、右が$A$による変換後の空間です。確かに、2次元から2次元に変換されていますね。このためこの行列のランクは2となります。ちなみに、行列の次元数とランクが等しいことをフルランク(full rank)と呼びます。
2.2. 2x2行列でランクが1の場合
次に、
$$
A=
(\mathbf{a}_1, \mathbf{a}_2) =
\left(
\begin{matrix}
2 & 3 \
1 & 1.5 \
\end{matrix}
\right)
$$
による変換を見てみます。
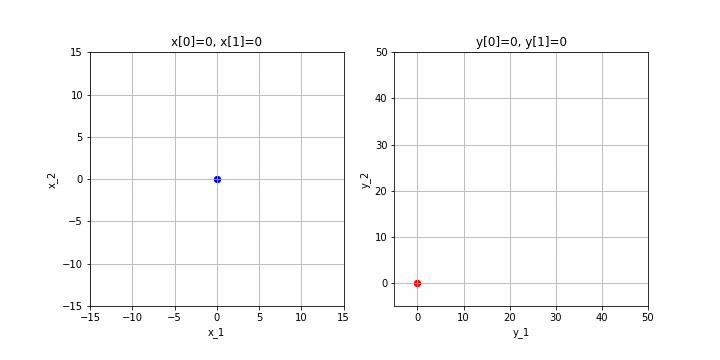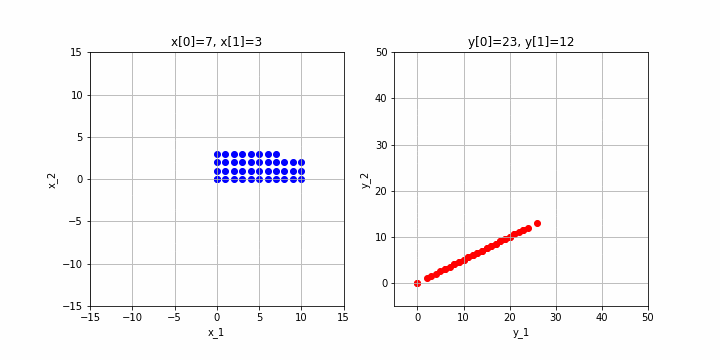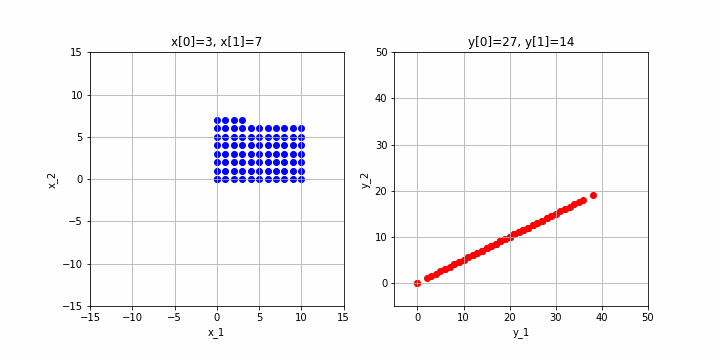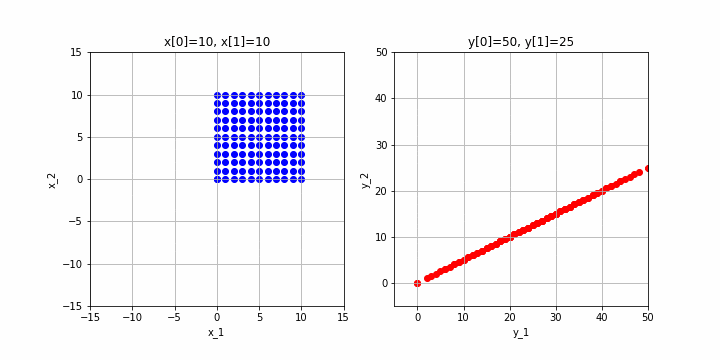
※クリックすると動画になるはずです。
変換先は直線になってしまいました。この場合は、変換先は2次元ですが、実際には全ての点が直線上(=1次元)に集まってしまうので、この行列のランクは1になります。
これは、第3回あたりでご説明したように、$\mathbf{a}_1$と$\mathbf{a}_2$の方向が同じになってしまうからですね。ちなみに、ご説明してなかったかも知れませんが、このような状態の時に、$\mathbf{a}_1$と$\mathbf{a}_2$は線形従属といいます。(逆に、2.1の例のように$\mathbf{a}_1$と$\mathbf{a}_2$が異なる向きのときは、$\mathbf{a}_1$と$\mathbf{a}_2$は線形独立であるといいます。)
2.3. 2次元から3次元への変換の場合(3x2行列の場合)
次に、2次元のベクトルを3次元のベクトルに変換する場合を考えます。この場合は、つまり、3x2行列を考えるということになります。(変換元のベクトルの次元が行列の列数に、変換後のベクトルの次元が行列の行数に現れますので。)
例として、
$$
A=\left(
\begin{matrix}
2 & 1 \
1 & 4 \
0 & 3 \
\end{matrix}
\right)
$$
による変換を考えてみます。
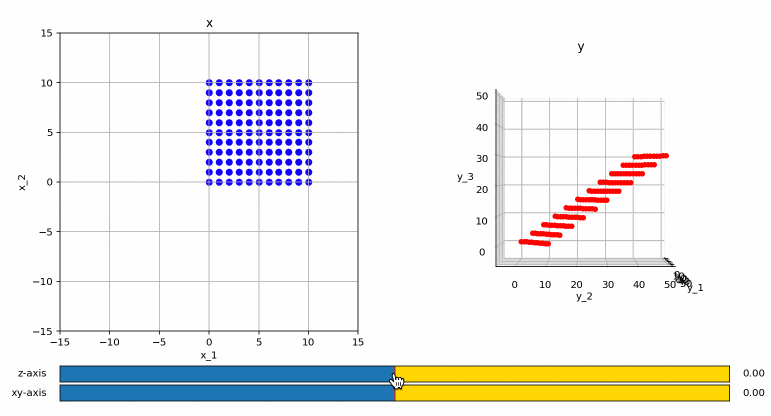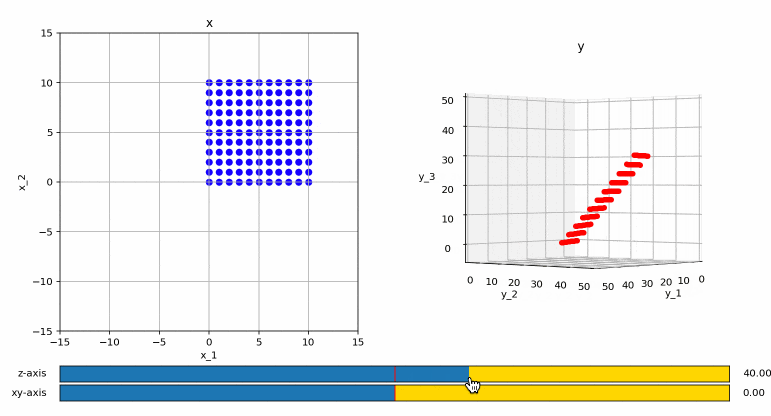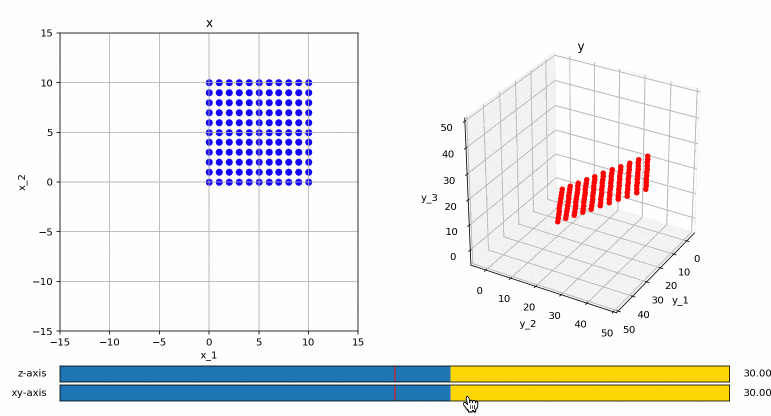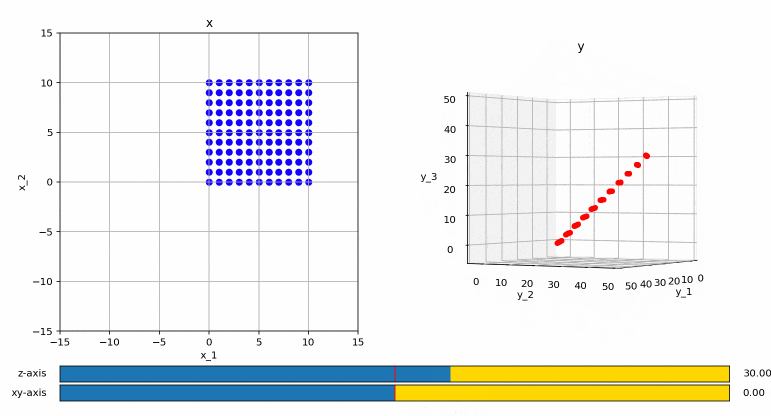
少し分かりにくいかも知れませんが、変換後のベクトルは3次元ですが、変換後の点はすべて3次元中の平面の中に収まっていることが分かります。これは、まあ、よく考えると当たり前で、元々が2次元の点なので、どう頑張っても3次元上の点にはならないですね。(平面上の絵から、3次元の立体を復元しようとしているみたいなものですので!)
ということで、この行列のランクは2ということになります。このように、行数より列数の方が小さい行列のランクは、どう頑張っても列数よりも大きくなることはありません。
2.4. 2x3行列でランクが1となる例
では、このような場合は、ランクは必ず列数と等しくなるのかというと、そういう訳でもありません。例えば、次の例は、3x2の行列ですが、ランクは1になる例となります。
$$
A=\left(
\begin{matrix}
2 & 3 \
1 & 1.5 \
0.5 & 0.75 \
\end{matrix}
\right)
$$
これまで同様、左が変換前、右が変換後となります。
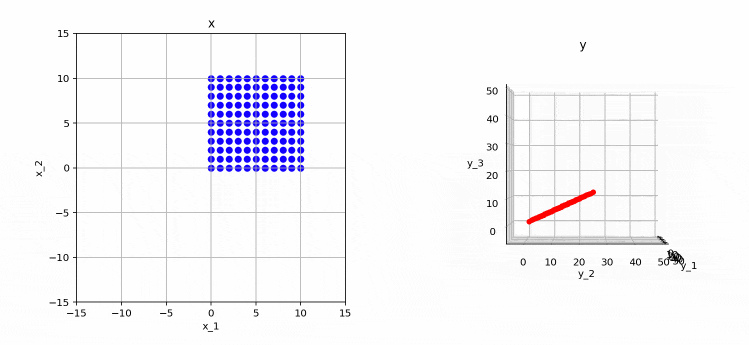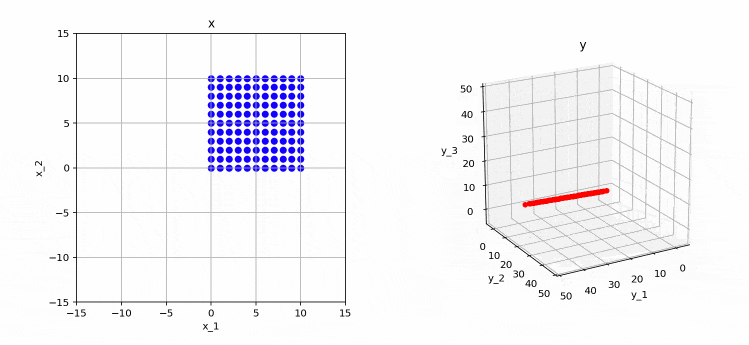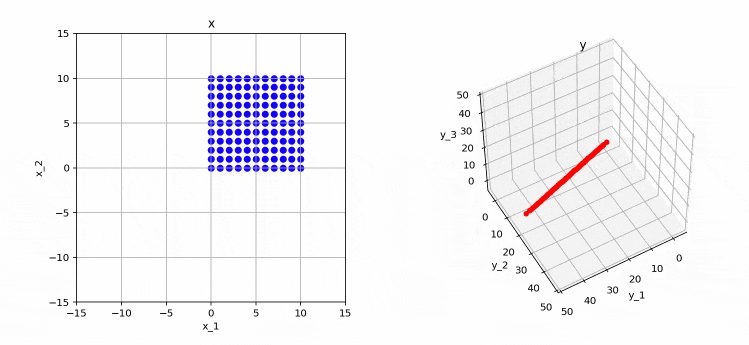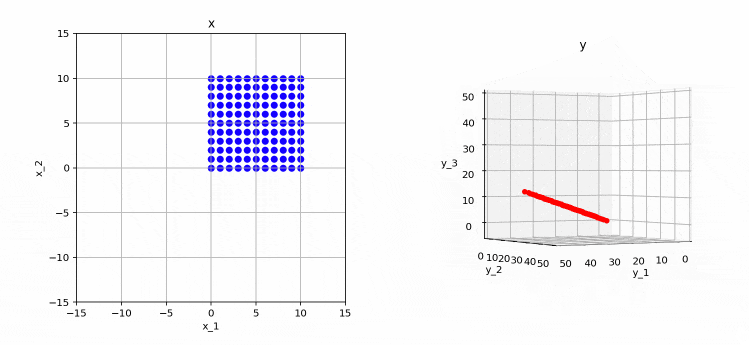
このように、変換後の点は3次元空間上の直線(=1次元)になっていることが分かります。つまり、この行列のランクは1であることが分かります。この場合も、先ほどの例と同じように、変換後の基底ベクトル(行列の各行列)が同じ向きになってしまっていることが原因となります。
2.5. 3次元から3次元への変換(3x3行列)の例
次に、考え方は同様なのですが、3x3の行列の例も見てみましょう。
2.5.1. フルランクの例
次の行列の変換前後の点を見てみましょう。
$$
A=\left(
\begin{matrix}
2 & 1 & 2\
1 & 4 & 3\
3 & 4 & 1\
\end{matrix}
\right)
$$
次の図は、3次元上の点(0,0,0)〜(1,1,1)を、上記行列で変換した時の変換前後の点を表しています。
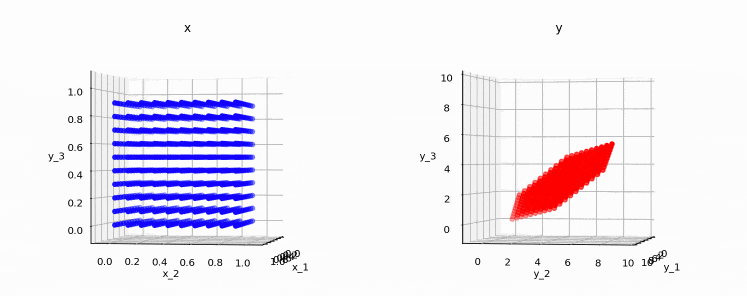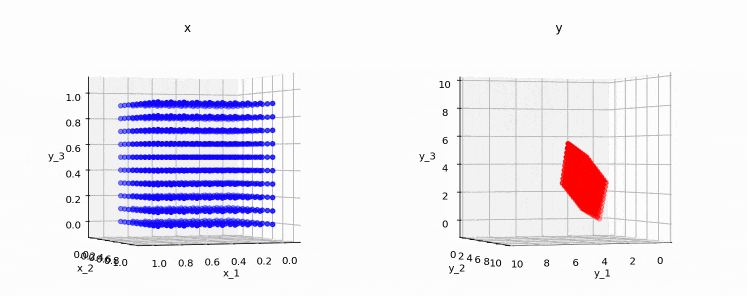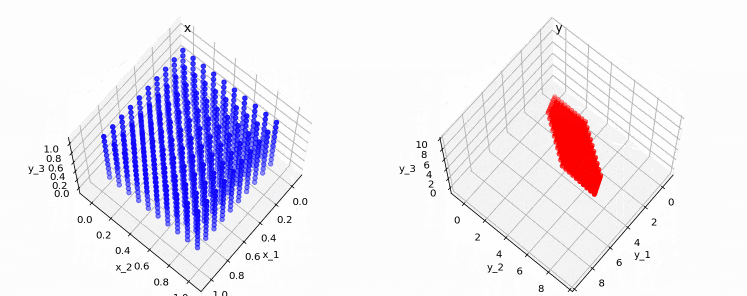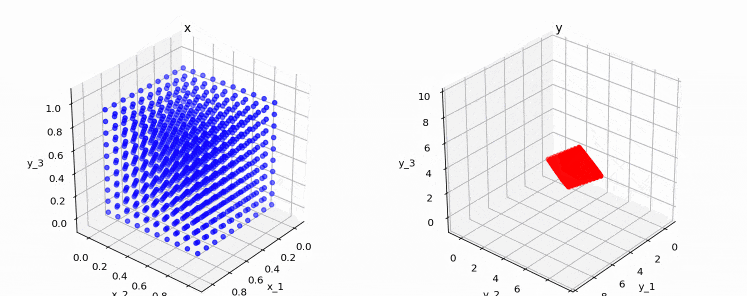
またちょっと分かりにくいかも知れませんが、変換後の点(右の図)も3次元であることが分かります。このため、この行列はフルランクとなります。
2.5.2. ランクが2の例
$$
A=\left(
\begin{matrix}
1 & 1 & 2\
2 & 3 & 5\
3 & 5 & 3\
\end{matrix}
\right)
$$
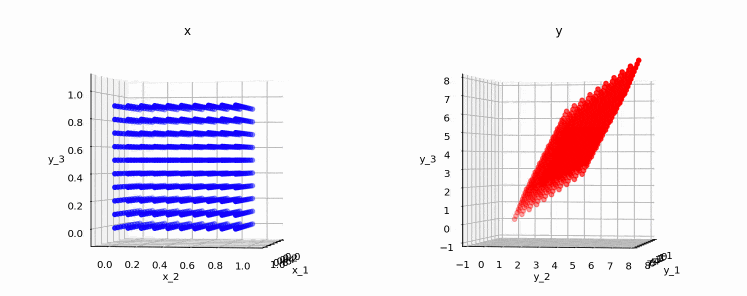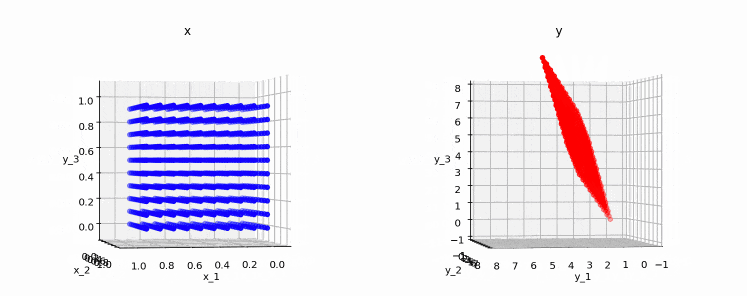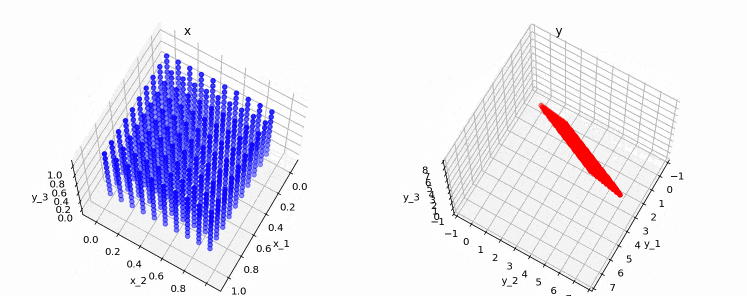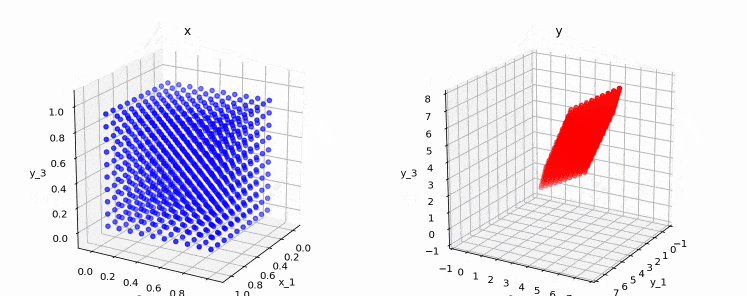
変換後の点(右の図)は、3次元空間上の平面(=2次元)に収まっていることが分かります。このため、この行列のランクは2となります。
2.6. 列の方が小さい行列(例えば、2x3行列)
この場合は、より小さい次元への変換になります。例えば、2x3の行列でしたら、3次元空間を2次元に変換するということですね。この場合は、当たり前ですが、ランクは2よりは小さくなります(変換後の点は2次元以上は考えていないので)。また、この場合でも、変換後の点が直線になるような場合は、ランクはさらに小さくなり、1になります。(すみませんが、疲れたので図示は省略します。)
2.7. n次元の例
これまで同様、$n$次元はイメージできません。ただ、何度も繰り返しですみませんが、$n$次元は2次元・3次元のイメージと同じですね!
4. まとめ
私も昔最初に線形代数を勉強した頃に、ランク=行列の次元数じゃないのか!?どう違うのか??と思ったのですが、今回の説明でご理解いただけましたでしょうか?最後に行列の次元数とランクの関係をまとめると以下のようになります。
(文章で書いただけですと分かりにくいかも知れませんが、これまでの図も合わせてご参照下さい。そもそも行列の行と列がこんがらがるかも知れませんが、そこは我慢してよ〜く考えてみて下さい。。)
- 行と列が等しい、かつ、変換後の点が次元上にめいいっぱい散らばっている場合 →フルランク。ランク=列数=行数
- 列と行が等しい、かつ、変換後の点は次元の一部にしか散らばっていない場合(=平面のイメージ) →ランク<列数=行数
- 行数>列数、かつ、変換後の点が次元上にめいいっぱい散らばっている場合 →ランク=列数<行数
- 行数>列数、かつ、変換後の点は次元の一部にしか散らばっていない場合 →ランク<列数<行数
- 行数<列数、かつ、変換後の点が次元上にめいいっぱい散らばっている場合 →ランク=行数<列数
- 行数<列数、かつ、変換後の点は次元の一部にしか散らばっていない場合 →ランク<行数<列数
次回は、逆行列について説明をしようと思っています。