LoginSignup
24
8

More than 3 years have passed since last update.

DiverseAdvent Calendar 2019Day 12diverse
@nog(Shingo Noguchi)

ポケモンしりとり(ピカチュウ→ミュウVer.)を最短にする

Last updated at Posted at 2019-12-12

Diverse Advent Calendar 2019 12日目の記事です。

最近最新作の発売されたポケモンの名前でしりとりをしてピカチュウからミュウまで最短何手でいけるのか。
またどのポケモンからどのポケモンの最短手数が一番多いのかを調べていきたいと思います。

なんでやろうと思ったの？

AdventCalender圧を受けて一番最初に思いついたのがこれだったので

新しく始まったアニメシリーズ「ポケットモンスター」のED主題歌でテクノ風のサウンドに合わせてポケモンの名前でしりとりをする「ポケモンしりとり (ピカチュウ→ミュウVer.) 」を聞いて非常に感銘を受けしりとりの生成に興味を持ったので

誰の役にも立たない記事を書きたい気持ちが強かった。

単語リスト生成(ポケモン一覧取得)

どこかポケモンの一覧がまとまっているところからプログラムで取得してテキストファイル化することにします。

ポケモンWikiさんのポケモン一覧が良さそうなので使わせて頂くことにします。

上記のようなプログラムから扱いやすそうなデータも存在したのですが、現時点では最新のソード＆シールドのポケモンに対応していない状態＆必要なのは名前だけなので今回は利用しないことにしました。
プレイヤーコミュニティでこういう情報が整備されていることにポケモンというゲームの凄さを感じます。

Wikiなのでhtmlの構造化等はあまりされてなさそうなのでザクッとスクレイピングします。

require 'open-uri'
require 'nokogiri'
require 'json'

DATA_URL="https://wiki.xn--rckteqa2e.com/wiki/%E3%83%9D%E3%82%B1%E3%83%A2%E3%83%B3%E4%B8%80%E8%A6%A7"
html = URI.open(DATA_URL).read
doc = Nokogiri::HTML.parse(html)
list = doc.css('.mw-parser-output table.sortable tbody tr td:nth-child(2)>a').map(&:content)
puts JSON.pretty_generate(list.uniq)

この部分は

  • ここは使い捨てなのでGoogleChromeのデベロッパーツールを見つつザクッと必要な情報を取るコードにする
  • 吐き出すデータは人間が見ることもあるので、pretty_generateにしておく

くらいしか意識したことはないです。
出力されたJSONのリストのサイズとポケモン図鑑のIDの最後の数が一致しているので大丈夫だと思いましょう。

ポケモンデータの正規化

取得したJSONをザッと目で見ているとポケモンの名前は全てがカタカナで作られているわけではなくデータの正規化が必要なことがわかります。

一旦ここではしりとりのルールに関しては考えずにカタカナの読みのデータを作成するところだけ考えます。
ニドラン♀=>ニドランメス
みたいな変換をしていきます。

require "json"

# ポケモンデータを扱う
module Pokemon
  # 機械的に変換できない奴ら
  CONVERT_MAP = {
    "ニドラン♂" => "ニドランオス",
    "ニドラン♀" => "ニドランメス",
    "ポリゴン2" => "ポリゴンツー",
    "ポリゴンZ" => "ポリゴンゼット",
  }.freeze

  # 読みとしては削除する文字列
  REMOVE_REGEXP = /[:・]/.freeze

  def self.names
    JSON.parse(open("./data/pokemon_names.json").read)
  end

  def self.need_convert?(name)
    !name.match(/^[\p{katakana}ー]+$/)
  end

  def self.name_to_yomi(name)
    yomi = name.dup
    yomi.gsub!(REMOVE_REGEXP, "")
    yomi = CONVERT_MAP[name].dup if need_convert?(yomi)
    yomi
  end

  def self.list
    names.map do |name|
      {
        word: name,
        yomi: name_to_yomi(name),
      }
    end
  end
end

しりとりのルール

これをきちんと決めないと実装できないので決めます。

  • ー（伸ばし棒は前の文字を最後の文字とする)
  • 濁音半濁音は別の文字として扱う
  • 小文字は大文字と同じものとして扱う

しりとりに使うデータとしての正規化

ルールを定めたことで先程のポケモンデータの正規化では不十分なことがわかるので、そこも扱いやすいものにします

伸ばし棒の削除と、小文字の変換データとして扱いやすいように最初の文字と最後の文字を持ったハッシュを作ります。

# 単語情報のハッシュのNormalizer
module Word
  def self.normalize(word)
    normalized_yomi = normalize_yomi(word[:yomi])
    {
      word: word[:word],
      yomi: word[:yomi],
      normalized_yomi: normalized_yomi,
      first: normalized_yomi[0],
      last: normalized_yomi[-1],
    }
  end

  def self.normalize_yomi(word)
    word = word.dup
    word.gsub!(/ー/, "")
    word.tr!("ァィゥェォヵヶッャュョヮ", "アイウエオカケツヤユヨワ")
    word
  end
end

実装

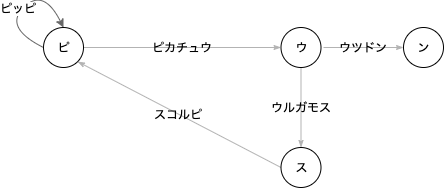
しりとりというのは文字を点とした経路の問題であると考える。
ピカチュウは「ピ」という点から「ウ」という点への移動。
と考えると
ピカチュウ→ミュウの最短化とは
ウ→ミの最短経路問題と考える事ができます。

shiritori.png

移動コストも全て一定なので、これなら高校数学位までしか数学知識のない自分でも簡単に解くことが出来そうです。
移動コストが一定のためノードX→ノードYの最短ルートはノードYのとなりのノードZまでの移動ルートに１単語分移動したものという法則が成り立つため
最長でも使われている文字数分のループで実現可能な文字X→Yの移動ルートを計算できるはずです。

仮想単語の作成

しりとりに置いて必要なのは最初の文字と最後の文字だけなため、
ライチュウとライコウは全く同じデータとなります。
その部分を同一のWord群として扱えるようVWordというものを作ります。

class VWord
  @list = []
  attr_reader :first, :last

  class << self
    attr_reader :list
  end

  def initialize(word)
    @first = word[:first]
    @last  = word[:last]
  end

  def self.get(word)
    obj = @list.find do |vword|
      vword.first == word[:first] &&
        vword.last == word[:last]
    end
    return obj if obj

    obj = new(word)
    @list.push obj
    obj
  end

  # 結果出力用
  # リアルWord一覧からこのVWordに属するもの一覧を出す
  def find_words(list)
    list.find_all do |word|
      word[:last] == self.last &&
        word[:first] == self.first
    end
  end

  def find_words_for_print(list)
    words = find_words(list)
    if words.size > 1
      "(#{words.join("|")})"
    else
      words[0][:word]
    end
  end
end

最短経路を算出する

ピカチュウ→ミュウの最短経路を探すだけであればピカチュウからミュウにたどり着くまでを幅優先で探索していけばすぐ見つかるとは思うのですが、今回は最長の最短経路になるポケモンしりとりを探すという目的もあるため、
ノード間の最短距離マップを作成します。

# 特定の文字から特定の文字の最短距離を生成する

class DMap
  attr_reader :map

  def initialize(vwords)
    # 最短経路に置いて最初の文字と最後の文字が同じ情報は不要
    # むしろ存在するとピッピ→ピクシーのような経路を探す時に自身を含んでしまう
    @vwords = vwords.find_all{|v| v.first != v.last }
    @chars = vwords.map {|v| [v.first, v.last] }.flatten.uniq.sort
    @map = {}
    @chars.each do |f|
      @map[f] = Hash.new nil
    end
    vwords.each do |vw|
      @map[vw.first][vw.last] = { length: 1, list: [[vw]] }
    end
    _fill
  end

  def _fill(length = 1)
    filled = false
    # 既存の最短経路に1単語を追加し未発見の新しい最短経路を埋めていく
    @map.keys.each do |first|
      @map[first].keys.each do |last|
        d = @map[first][last]
        unless d[:length] == length
          next
        end

        @vwords.each do |vw|
          if last != vw.first
            next
          end

          new_d = @map[first][vw.last]
          # 今作成しようとしている経路より短ければ無視
          # 同じ長さの経路の場合両方のパターンを記録
          if new_d && new_d[:length] < (length + 1)
            next
          end

          unless new_d
            new_d = {
              length: length + 1,
              list: [],
            }
          end
          new_d[:list].push(*d[:list].map {|l| l + [vw] })
          @map[first][vw.last] = new_d
          filled = true
        end
      end
    end
    # 一つも新しい最短経路が発見されなかった場合これ以上必要な経路は存在しない
    unless filled
      return
    end

    _fill(length + 1)
  end
end

しりとりが不可能なポケモンたち

ポケモンしりとりのルートを作成不可能なポケモンについても調べてみます。

まずシンプルに繋がるかどうかをコード書いて調べてみます。

vlist = VWord.list.find_all{|vw| vw.first != vw.last }
p vlist.map(&:first).uniq - vlist.map(&:last).uniq
p vlist.map(&:last).uniq - vlist.map(&:first).uniq

["ペ", "ハ", "ヘ", "ホ", "セ"]
["ン"]

ピッピ、ポッポ等の始まりと終わりの文字が同じポケモンはこの探索に無意味なので除外しています。
（除外しないとホーホーの存在により「ホ」がヒットしません。

["ペ", "ハ", "ヘ", "ホ", "セ"]　これらの文字で終わるポケモンが存在しないため、これらの文字で始まるポケモンはしりとりへの参加が難しいようです。

ンから始まるポケモンはそんざいしないため、どのポケモンも最低一つのポケモンとしりとりで繋がることは可能なようです。

これらの条件に当てはまるポケモンも出力してみます。

["ペルシアン", "ハクリュー", "ハネッコ", "(ハガネール|ハンテール)", "(ハリーセン|ハリマロン)", "ハッサム", "ヘラクロス", "ヘルガー", "ハピナス", "ホウオウ", "セレビィ", "(ハスボー|ハトーボー)", "ハスブレロ", "ペリッパー", "ハリテヤマ", "ホエルコ", "ホエルオー", "ハブネーク", "ヘイガニ", "ハヤシガメ", "ペラップ", "ハーデリア", "(ハハコモリ|ハギギシリ)", "ホイーガ", "ペンドラー", "ハリボーグ", "ホルビー", "ホルード", "ペロッパフ", "ペロリーム", "ホシガリス", "セキタンザン"]

意外といますね。ポケモンしりとりverピカチュウ→ホウオウは現在のポケモンの種類では実現不可能なので第9世代に「ホ」で終わるポケモンが登場することを期待しましょう。

ピカチュウ→ミュウはどこまで短くできるのか

今まで書いたコードでピカチュウからミュウの最短ルートを調べてみます。

def create_routes(start_str, goal_str)
  @words ||= Pokemon.normalized_list
  start = @words.find {|word| word[:word] == start_str }
  goal = @words.find {|word| word[:word] == goal_str }
  words = @words.find_all {|word| word[:last] != word[:first] } - [start, goal]
  @stock ||= VWord.create_stock(@words)
  @dmap ||= DMap.new(VWord.list)
  {
    start: start,
    goal: goal,
    routes: @dmap.map.dig(start[:last], goal[:first]),
    words: words
  }
end

def print_route(routes)
  puts "---"
  puts "#{routes[:start][:word]} => #{routes[:goal][:word]} route"
  unless routes[:routes]
    puts "routes not found"
    return
  end
  puts "Length: #{routes[:routes][:length]}"
  routes[:routes][:list].each do |route|
    puts route.map {|vw| vw.find_words_for_print(routes[:words]) }.join(" => ")
  end
end

print_route(create_routes("ピカチュウ", "ミュウ"))

ピカチュウ => ミュウ route
Length: 2
ウルガモス => (スターミー|スボミー)

間に二匹のポケモンを挟むだけで終わることができるようです。
EDテーマも一瞬で終わることができますね。時短です。

最短経路が一番長いポケモンしりとりはなんなのか

これに関しては非常に長いパターンになるのは5個のポケモンを間に挟むパターンだということがわかりました。

これは今後ポケモンの種類が増えることで更に短くなっていくものと思われます。

上記の["ペ", "ハ", "ヘ", "ホ", "セ"]で始まるポケモンを覗いてしりとりとして繋がらないポケモンとポケモンのペアは存在しませんでした。

そのパターンをこのようなコードで出してみます。

@dmap.map.each do |first, map|
  map.each do |last, result|
    if result[:length] >= 5
      p [first, last, result[:length]]
    end
  end
end

# スタートのポケモンの最後の文字, ゴールのポケモンの最初の文字, 間に挟まるポケモンの数
["ギ", "ソ", 5]
["グ", "ソ", 5]
["ゲ", "ギ", 5]
["ゲ", "ザ", 5]
["ゲ", "エ", 5]
["ゲ", "ゾ", 5]
["ズ", "ザ", 5]
["ズ", "ベ", 5]
["ズ", "ソ", 5]
["ズ", "エ", 5]
["セ", "ゾ", 5]
["セ", "ソ", 5]
["ソ", "エ", 5]
["ゾ", "ソ", 5]
["ト", "エ", 5]
["パ", "ソ", 5]
["ピ", "ソ", 5]
["プ", "ギ", 5]
["プ", "ゾ", 5]
["プ", "エ", 5]
["ヘ", "ザ", 5]
["ヘ", "エ", 5]
["ヘ", "ソ", 5]
["ヨ", "ソ", 5]
["ロ", "ソ", 5]

このパターンについては非常に膨大になるので
この中の一つであるヒトカゲ→ギャロップの経路だけ示します。

ヒトカゲ => ギャロップ route
Length: 5
(ゲンガー|ゲッコウガ) => ガーディ => イルミーゼ => ゼブライカ => (カモネギ|カミツルギ)
ゲコガシラ => ラクライ => イルミーゼ => ゼブライカ => (カモネギ|カミツルギ)
(ゲンガー|ゲッコウガ) => (ガブリアス|ガメノデス|ガチゴラス) => スバメ => メブキジカ => (カモネギ|カミツルギ)
ゲノセクト => (トロピウス|トリデプス|トゲキッス|トルネロス) => スバメ => メブキジカ => (カモネギ|カミツルギ)
ゲコガシラ => (ラプラス|ラルトス|ラブカス|ラティアス|ラティオス|ランクルス|ランドロス|ラランテス) => スバメ => メブキジカ => (カモネギ|カミツルギ)
ゲコガシラ => ラッキー => キャモメ => メブキジカ => (カモネギ|カミツルギ)
(ゲンガー|ゲッコウガ) => (ガブリアス|ガメノデス|ガチゴラス) => ストリンダー => ダルマッカ => (カモネギ|カミツルギ)
ゲノセクト => (トロピウス|トリデプス|トゲキッス|トルネロス) => ストリンダー => ダルマッカ => (カモネギ|カミツルギ)
ゲコガシラ => (ラプラス|ラルトス|ラブカス|ラティアス|ラティオス|ランクルス|ランドロス|ラランテス) => ストリンダー => ダルマッカ => (カモネギ|カミツルギ)
ゲコガシラ => ラフレシア => アギルダー => ダルマッカ => (カモネギ|カミツルギ)
ゲコガシラ => ラグラージ => ジャローダ => ダルマッカ => (カモネギ|カミツルギ)
ゲノセクト => トゲピー => ピクシー => シキジカ => (カモネギ|カミツルギ)
ゲコガシラ => ラッタ => タマザラシ => シキジカ => (カモネギ|カミツルギ)
ゲコガシラ => ラフレシア => アゴジムシ => シキジカ => (カモネギ|カミツルギ)
ゲコガシラ => ラムパルド => ドデカバシ => シキジカ => (カモネギ|カミツルギ)
ゲノセクト => トゲチック => クヌギダマ => マーイーカ => (カモネギ|カミツルギ)
ゲコガシラ => ラッタ => (タマタマ|タチフサグマ) => マーイーカ => (カモネギ|カミツルギ)
ゲコガシラ => ラフレシア => アメタマ => マーイーカ => (カモネギ|カミツルギ)
ゲコガシラ => ラッキー => キテルグマ => マーイーカ => (カモネギ|カミツルギ)
ゲコガシラ => ラグラージ => ジグザグマ => マーイーカ => (カモネギ|カミツルギ)

本当は最長経路を出したかった

本当は最短経路とそれの１０倍位難しそうな最長経路を出すという問題に取り掛かりたかった。
いや取り掛かったんですが、数学的知識が足りずその部分を調べながらやろうとしたのです。
するとすぐにソルバーを使用してそのまんまポケモンしりとりの最長を見つけ出すコードが見つかりました。
単に写経したに過ぎなかったので記事からは外しました。

その際に参考になった記事をいくつか貼っておきます
https://qiita.com/YSRKEN/items/543938ba6a0fcb46e38d
https://qiita.com/SaitoTsutomu/items/ba2dedb5795cae36f8a1
http://auemath.aichi-edu.ac.jp/~ykhashi/semi/2010note/08_issey_final.pdf

得られたメリット

  • 最長経路問題を解こうとしたときに自分の腕力の足りなさを知れた
  • 簡単なコードでコードを書くことに対してのハードルが全く無かったので、いつか試そうと思ってたこと試せた
    • github actions使ってみれた
    • VSCodeのRemoteでコンテナ内開発やってみれた

特に腕力のなさに対しては致命的に感じたので、ある程度の数学的知識と周辺ツールを使えるくらいは勉強するべきだなと思いました

また昨日の弊社アドベントカレンダー記事を読んでGraphDBを利用した形で問題を解くのも面白そうだと思ったのでこちらも後日試してみたいなと思います。

24
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
24
8