C++とEigenで状態方程式を解いてopenFrameworksで表示する。

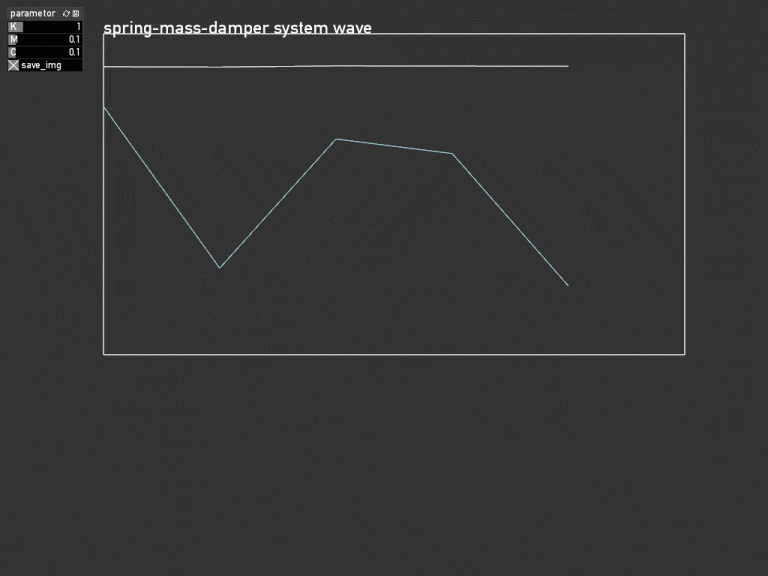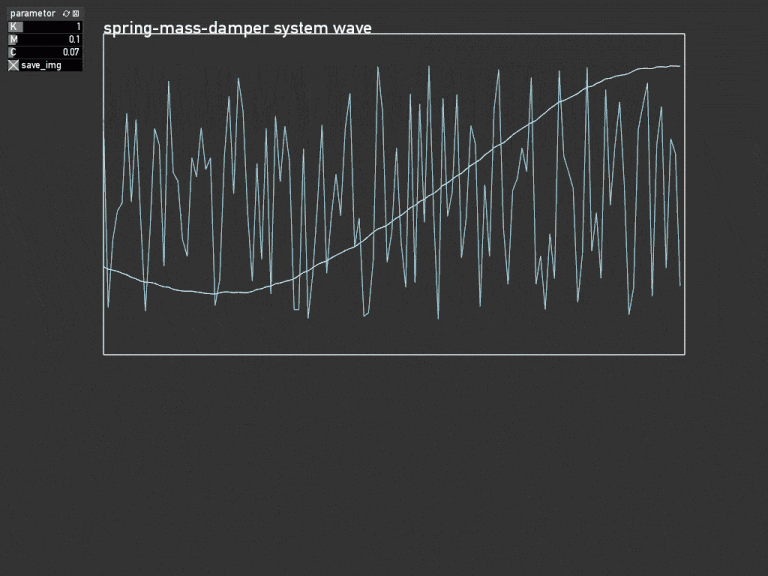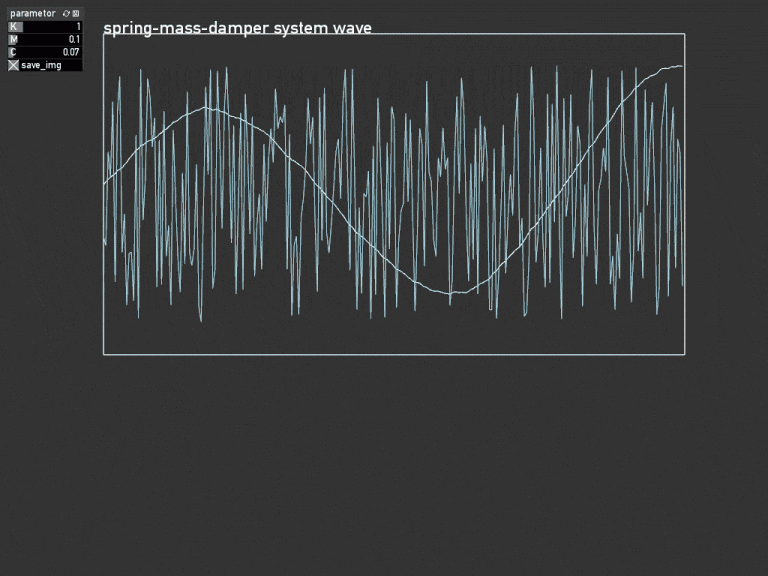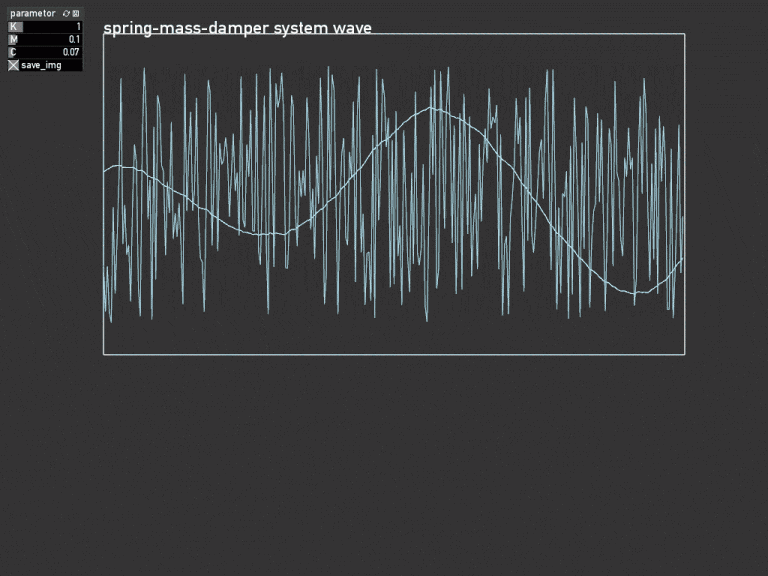
目的

C++言語＋Eigenとで、バネ～マス～ダンパ系の状態方程式の応答を求め、
openFrameworksのaddon ofxGraphで応答波形をリアルタイムに表示する。
また、ofxGuiでバネ～マス～ダンパのパラメータをリアルタイムに変更できるようにする。

参考：C++とEigenで状態方程式を解く。

　

事前準備

以下をインストールしておく。
・openFrameworks
　→上記ページからファイルをダウンロードし、任意のフォルダに展開する。
・ofxGraph
　→上記ページからファイルをダウンロードし、openFrameworksのaddonディレクトリ以下に配置する。
・Eigen
→上記ページからヘッダファイルをダウンロードし、openFrameworksのプロジェクトのsrcディレクトリ以下に配置する。

実装

以下のバネ～マス～ダンパ系の状態方程式を解くとする。
u(t)には外乱としてホワイトノイズを注入する。

\dot{x}(t)=Ax(t)+Bu(t) \\
y(t)=Cx(t)+Du(t)

x(t)=
\begin{bmatrix}
x_{1}  \\
x_{2}  
\end{bmatrix}

,
u(t)=f
,

A=
\begin{bmatrix}
0 & 1 \\
-k/m & -c/m
\end{bmatrix}
,
B=
\begin{bmatrix}
0 \\
1/m 
\end{bmatrix}
,
C=
\begin{bmatrix}
1 & 0 
\end{bmatrix}
,
D=[0]

サンプルソース

ofApp.cpp

#include "ofApp.h"

void RungeKutta(MatrixXd dX, MatrixXd &X, MatrixXd u, double tt, double dt, MatrixXd A, MatrixXd B, MatrixXd C, MatrixXd D) {
    MatrixXd k1 = A*X + B*u;
    MatrixXd k2 = A*(X + 0.5*k1*dt) + B*u;
    MatrixXd k3 = A*(X + 0.5*k2*dt) + B*u;
    MatrixXd k4 = A*(X + k3*dt) + B*u;
    MatrixXd k = (k1 + 2.0*k2 + 2.0*k3 + k4)*dt / 6.0;
    X = X + k;
}
void ofApp::setup(){
    ofSetVerticalSync(true); 
    ofxGuiSetFont(ofToDataPath("ofxGraph/DIN Alternate Bold.ttf"), 10);
    graph.setup(100, 100, 800, 400);
    graph.setName("spring-mass-damper system wave"); 
    graph.setDx(2.0);
    graph.setColor(ofColor::white); 
    graph.setBufSize(1000);  
    graph.setLabel({ "y0","u" });
    frame = 0;

    gui.setup("parametor");
    gui.add(kk.setup("K", 1.0, 0.0, 5.0));
    gui.add(mm.setup("M", 0.1, 0.0, 1.0));
    gui.add(cc.setup("C", 0.1, 0.0, 1.0));

    AA.resize(2, 2);
    AA << 0, 1, -kk / mm, -cc / mm;
    BB.resize(2, 1);
    BB << 1, 1 / mm;
    CC.resize(1, 2);
    CC << 1, 0;
    DD.resize(1, 1);
    DD << 1;

    XX.resize(2, 1);
    XX(0, 0) = 0;
    XX(1, 0) = 0;
    dXX.resize(2, 1);
    dXX(0, 0) = 0;
    dXX(1, 0) = 0;

    uu.resize(1, 1);
    uu << 0;
    YY.resize(1, 1);
    YY(0, 0) = 0;

    dt = 0.01;
    tt = 0.0;
}

//--------------------------------------------------------------
void ofApp::update() {
    frame++;

    AA << 0, 1, -kk / mm, -cc / mm;
    BB << 1, 1 / mm;

    double TT = 100.0;
    uu(0, 0) = ofRandom(-1,1);

    RungeKutta(dXX, XX, uu, tt, dt, AA, BB, CC, DD);
    YY = CC*XX;
    tt += dt;

    vector<float>value;
    value.push_back(YY(0, 0));
    value.push_back(uu(0,0));
    graph.add(value);

}

void ofApp::draw(){
    ofBackground(50, 50, 50);
    gui.draw();
    graph.draw();
}

ofApp.h

#include "ofMain.h"
#include "ofxGraph.h"
#include "ofxGui.h"

#define _USE_MATH_DEFINES
#include <math.h>

#include "Eigen/Dense"
#include "Eigen/Core"
#include <iostream>
#include <fstream>

using namespace Eigen;
using namespace std;

class ofApp : public ofBaseApp{
    public:
        void setup();
        void update();
        void draw();
        ofxGraph graph;
        long frame;
        ofxPanel gui;
        ofxFloatSlider kk,mm,cc;
        MatrixXd AA;
        MatrixXd BB; 
        MatrixXd CC;
        MatrixXd DD;
        MatrixXd XX;
        MatrixXd dXX;
        MatrixXd uu;
        MatrixXd YY;
        double dt ;
        double tt ;
};

ソースは以下にも格納済み。
https://github.com/nnn112358/180217_system_control