C++とEigenで状態方程式を解く。

#目的
C++言語とEigenとで、1自由度系(バネマスダンバ系)の状態方程式を解く。

PythonControlで初期条件応答を求める。をC++に移植する。

#事前準備
Eigenをインストールする。
上記ページからヘッダファイルをダウンロードし、読み込むだけでコンパイルすることができる。
Eigenは、C++言語で行列・ベクトルを扱うためのライブラリである。
C++で現代制御をプログラミングする場合、制御システムをベクトル行列で扱う為、Eigenを使うことでプログラミングを作成しやすくできる。

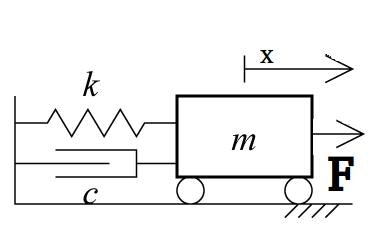
#システムのモデル化

m:質量[kg]
k:ばね定数[N/m]
c:粘性減衰係数[N・s/m]
f：力[N]

以下の状態方程式を立式する。

\dot{x}(t)=Ax(t)+Bu(t) \\
y(t)=Cx(t)+Du(t)

x(t)=
\begin{bmatrix}
x_{1}  \\
x_{2}  
\end{bmatrix}

,
u(t)=f
,

A=
\begin{bmatrix}
0 & 1 \\
-k/m & -c/m
\end{bmatrix}
,
B=
\begin{bmatrix}
0 \\
1/m 
\end{bmatrix}
,
C=
\begin{bmatrix}
1 & 0 
\end{bmatrix}
,
D=[0]

#ルンゲクッタ法
状態方程式の時間応答はルンゲクッタ法で近似解を得ることができる。
ルンゲクッタ法を以下の式に示す。

\begin{eqnarray}
k_1&=&f(t,x)\\
k_2&=&f(t+\frac{Δt}{2}, x(t)+\frac{k_1Δt}{2})\\
k_3&=&f(t+\frac{Δt}{2}, x(t)+\frac{k_2Δt}{2})\\
k_4&=&f(t+Δt, x(t)+k_3Δt)\\
x(t+Δt)&=&x(t)+\frac{Δt}{6}(k_1+2k_2+2k_3+k_4)
\end{eqnarray}

これをEigenを使って、プログラミングすると、

void RungeKutta(MatrixXd dX, MatrixXd &X, MatrixXd u, double tt, double dt, MatrixXd A, MatrixXd B, MatrixXd C, MatrixXd D) {
	MatrixXd k1 = A*X + B*u;
	MatrixXd k2 = A*(X + 0.5*k1*dt) + B*u;
	MatrixXd k3 = A*(X + 0.5*k2*dt) + B*u;
	MatrixXd k4 = A*(X + k3*dt) + B*u;
	MatrixXd k = (k1 + 2.0*k2 + 2.0*k3 + k4)*dt / 6.0;
	X = X + k;
}

#サンプルソース
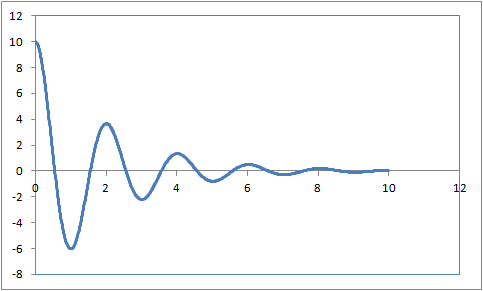
1自由度系(バネマスダンバ系)の伝達関数の初期条件応答を、ルンゲクッタ法から求める。
X=[10,0]からの初期条件応答を求める。

#include "Eigen/Dense"
#include "Eigen/Core"
#include <iostream>
#include <fstream>
using namespace Eigen;
using namespace std;

void RungeKutta(MatrixXd dX, MatrixXd &X, MatrixXd u, double tt, double dt, MatrixXd A, MatrixXd B, MatrixXd C, MatrixXd D) {
	MatrixXd k1 = A*X + B*u;
	MatrixXd k2 = A*(X + 0.5*k1*dt) + B*u;
	MatrixXd k3 = A*(X + 0.5*k2*dt) + B*u;
	MatrixXd k4 = A*(X + k3*dt) + B*u;
	MatrixXd k = (k1 + 2.0*k2 + 2.0*k3 + k4)*dt / 6.0;
	X = X + k;
}

int main() {
	double	k = 1.0;
	double	m = 0.1;
	double	c = 0.1;

	MatrixXd A(2, 2);
	A(0, 0) = 0;
	A(0, 1) = 1;
	A(1, 0) = -k / m;
	A(1, 1) = -c / m;
	MatrixXd B(2, 1);
	B(0, 0) = 1;
	B(1, 0) = 1 / m;

	MatrixXd C(1, 2);
	C(0, 0) = 1;
	C(0, 1) = 0;
	MatrixXd D(1, 1);
	D(0, 0) = 0;

	double dt = 0.01;
	double tt = 0.0;
	MatrixXd X(2, 1);
	X(0, 0) = 10;
	X(1, 0) = 0;
	MatrixXd dX(2, 1);
	dX(0, 0) = 0;
	dX(1, 0) = 0;
	MatrixXd u(1, 1);
	u(0, 0) = 0;
	MatrixXd Y(1, 1);
	Y(0, 0) = 0;

	double freq = 1.0;
	ofstream ofs("outdata.csv");
	ofs << "time," << "y" << endl;

	for (int i = 0; i < 1000; i++) {
		RungeKutta(dX, X, u, tt, dt, A, B, C, D);
		Y = C*X;
		ofs << tt << "," << Y(0, 0) << endl;
		tt += dt;
	}

	return 0;
}

#結果
以下の初期条件応答が得られる。

PythonControlで初期条件応答を求める。と全く同じグラフが得られた。