論文読み "Attention Is All You Need"

概要

• 今回紹介する論文
  • Attention Is All You Need
  • Google BrainやGoogle Researchの人たちが2017年6月に発表した。
    • (この記事で使用している図表は論文からの転載です。)
• 内容:
  • 新しい翻訳モデル(Transformer)の提案。既存のモデルよりも並列化に対応しており、短時間の訓練で高いBLEUスコアを達成した。
  • TransformerはRNNやCNNを使わず、attentionメカニズムに基づいている。
• 実装例:
  • Tensorflow
  • Chainer
• その他:
  • これまでのニューラル機械翻訳の発展や課題についてはニューラル機械翻訳の動向がわかりやすい。
  • より高い品質の翻訳を実現するGoogleの「Transformer」がRNNやCNNをしのぐレベルに
  • Transformer: A Novel Neural Network Architecture for Language Understanding
  • Accelerating Deep Learning Research with the Tensor2Tensor Library

Introduction

• 今までのNeural machine translation(NMT)はRNNやCNNを使っているものが多い。
• RNN(LSTM、GRU等)は文章(単語列)を前から順に入力とし、前の単語に依存する。
  • t番目の状態 $h_t$ を計算するために、t番目の単語とt-1番目の状態 $h_{t-1}$ を使用する。
• しかし、RNNだと並列化が難しく、特に文章が長いと計算時間が長くなる/メモリ使用量が多くなる。
  • メモリ使用量に関しては、"factorization tricks"や"conditional computation"といった研究がある。
• ほとんどすべての翻訳モデル等では、attention構造を入れることで精度の改善がされている。
• この論文で提案するTransformerはRNNやCNNを使わない。
• 論文のタイトルの通り、attention構造を使う。

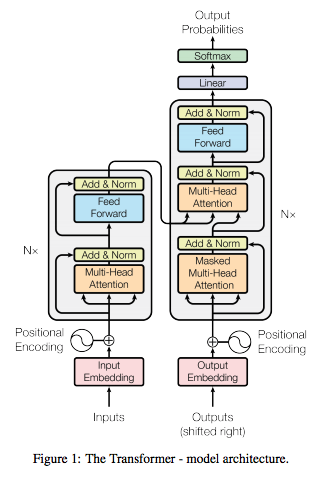
モデルの全体像

• エンコーダー・デコーダー構造を持つ。

エンコーダー

• 上図の左側。
• N個(=6)のlayerからなる。
• 各layerの下記の2個のsub-layerを持つ。(※詳細は後述)
  • multi-head self-attention mechanism
  • position-wise fully connected feed-forward network
• 各sub-layerのアウトプットは下記のようにresidual connectionとlayer normalizatonを行う。
  • $\text{LayerNorm}(x + \text{Sublayer}(x))$
• 各layerとembeddingアウトプットは $d_{\text{model}}$ 次元(=512)になる

デコーダー

• 上図の右側
• デコーダーもN個(=6)のlayerからなる。
• 各layerの下記の3個のsub-layerを持つ。(※詳細は後述)
  • masked multi-head self-attention mechanism
    • $i$ 番目の文字を予測するために、$i-1$ 番目までの文字のみを利用するようにマスクを行う。
  • multi-head attention mechanism
    • エンコーダーのアウトプットへのattentionを行う。
  • position-wise fully connected feed-forward network

データの流れ

エンコーダー

1. Input
   • 文字列 $\bar{w} = (w_1, w_2, ..., w_{N})$
   • ただし、$w_1=\text{bos}$ 、 $w_N=\text{eos}$
2. Endedding
   • $E = \text{Embed}(\bar{w}) \in R^{N \times d_{model}}$
3. Positional Encoding
   • $\bar{E} = \text{Positional}(E) \in R^{N \times d_{model}}$
4. Multi-head self-attention
   • $Q = f_Q(\bar{E}) \in R^{N \times d_k}$
   • $K = f_K(\bar{E}) \in R^{N \times d_k}$
   • $V = f_V(\bar{E}) \in R^{N \times d_k}$
   • $M = \text{MultiHead}(Q, K, V) \in R^{N \times d_{model}}$
5. Add & Norm
   • $\bar{M} = \text{LayerNorm}(\bar{E} + M) \in R^{N \times d_{model}}$
6. Position-wise fully connected feed-forward network
   • $F = \text{LayerNorm}(\bar{M}) \in R^{N \times d_{model}}$
7. Add & Norm
   • $\bar{F} = \text{LayerNorm}(\bar{M} + F) \in R^{N \times d_{model}}$

デコーダー

• エンコーダーとほぼ同じ。違いは1番目のsub-layerでmaskを行うこと、2番目でエンコーダーの結果からKとVを計算すること。
• Mask
  • Positional encodingの結果を $\bar{E} \in R^{N \times d_{model}}$ とする。
  • i 番目の単語の予測を行うとき、$\bar{E}$ の $i$ 行 から $L$ 行の要素すべてを0にする。

モデルの構成要素

• Transformerを構成する要素の紹介
• N を文章の長さとする。

Embedding

• 単語を $d_{model}$ 次元のベクトルで表す

Positional encoding

• RNNのようにモデルの構造が単語の順序関係を持っていないので、位置情報を付与する。
• 文章における単語の位置とembeddingの位置に依存して決まる。
• 奇数/偶数で分ける
  • $PE(pos, 2i) = \sin(pos/10000^{2i/d_{model}})$
  • $PE(pos, 2i+1) = \cos(pos/10000^{2i/d_{model}})$

Scaled dot-product attention

• $\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$
  • $Q \in R^{N \times d_k}$
  • $K \in R^{N \times d_k}$
  • $V \in R^{N \times d_v}$
  • $\text{Attention}(Q, K, V) \in R^{N \times d_v}$

Multi head attention

• $\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h) W^O$
  • $\text{head}_i = \text{Attention}(QW^Q_i, KW^K_i, VW^V_i)$
  • $W^Q_i \in R^{d_{model} \times d_k}$
  • $W^K_i \in R^{d_{model} \times d_k}$
  • $W^V_i \in R^{d_{model} \times d_v}$
  • $W^O \in R^{h d_{k} \times d_{model}}$
  • $\text{MultiHead}(Q, K, V) \in R^{N \times d_{model}}$

Multi head self attentionのQ, K, V

• Self-attention
  • 文字列に対してEmbeddingとPositionalEncodingを対したものをXとする。
    • $X \in R^{N \times d_{model}}$
  • $Q=f_Q(X)$
    • ${q_{ij}} = {a^Q_j x_{ij}}$
  • $K=f_K(X)$、$V=f_V(X)$ も$f_Q$と同じ。
• Attention
  • $Q=f_Q(X)$
  • $K=f_K(Z)$、$V=f_V(Z)$
    • $Z$ はencoderの出力結果

Position-wise feed-forward network

• $\text{FFN}(x) = \text{ReLU}(x W_1 + b_1)W_2 + b_2$

Training方法

ハードウェア

• 8 NVIDIA P100 GPUs
  • AWSでこれよりも高性能のGPUが使える。
  • 新インスタンス- NVIDIA Tesla V100 GPUを最大8個搭載したAmazon EC2インスタンス P3
  • V100のほうがP100よりも3倍程度速いらしい。
• 1ステップ約0.4秒。100,000ステップを12時間で学習
• big modelは1ステップ約1.0秒。300,000ステップを3.5日で学習

最適化手法

• Adam optimizerを仕様し、learning rateを下記のように調整
• $lrate = d_{model}^{-0.5} \min(step_num^{-0.5}, step_num \cdot warmup_steps^{-1.5})$

正則化

Residual dropout

• 各sub-layerに対してdropoutを行ってから、Add & Normを行う
  • $\text{LayerNorm}(x + \text{DropOut}(\text{Sub}(x), P_{drop}))$

Label smoothing

• モデルが出力するのは各単語に対する確率なので、{0, 1}の正解ラベルをスムージングする。
  • $q(k) = (1 - \epsilon) \delta_{k,y} + \frac{\epsilon}{K}$
  • Transformerでは、$\epsilon=0.1$としている。
• これによりperplexityは悪化したが、accuracyとBLEUは改善した。
• Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jonathon Shlens, and Zbigniew Wojna.
  Rethinking the inception architecture for computer vision. CoRR, abs/1512.00567, 2015.

パフォーマンスなど

各Layerの複雑さなど

• RNNやCNNによるattention構造との比較
  • layerごとの計算の複雑さ
  • 並列化できる計算の量
  • 長期依存のパスの長さ

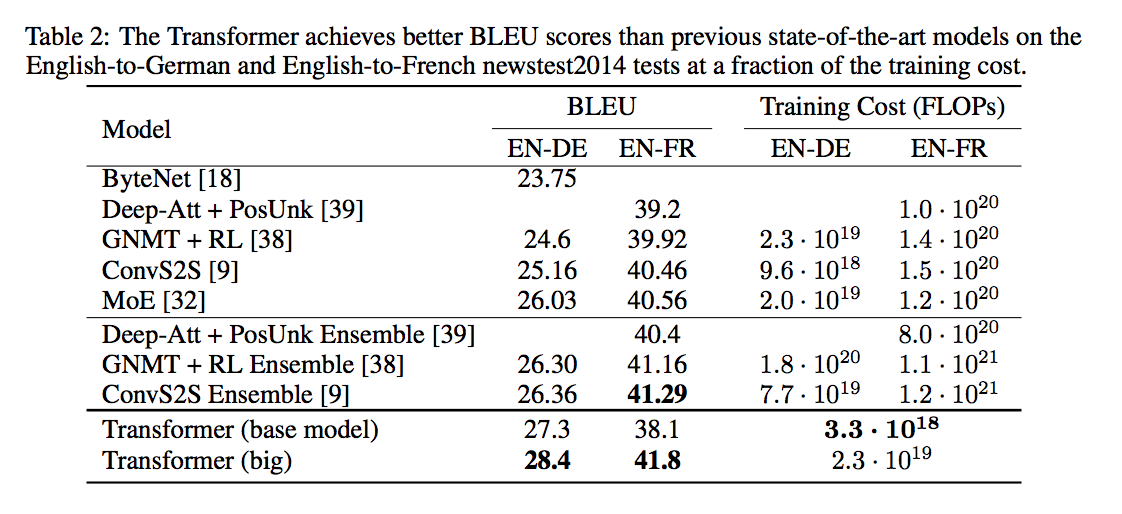
BLEUスコア

• English-to-Germanのケースデスはbase modelでも他の手法に比べ最高スコアを出している。big modelを使うことで更に精度が向上している。

実際に使ってみる

• 追記する。