(完全)準同型暗号の最前線２（原理編）: TFHEの原理 #5 Identity Key Switching

目次

1. (完全)準同型暗号の最前線1（入門編)
2. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #1 TLWE
3. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #2 TRLWE & SampleExtarctIndex
4. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #3 TRGSW & CMUX
5. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #4 Blind Rotate
6. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #5 Identity Key Switching←イマココ

初めに

これを説明すればHomNANDは今までの全部くっつけたら終わりですね。
もう１年が終わってしまう......

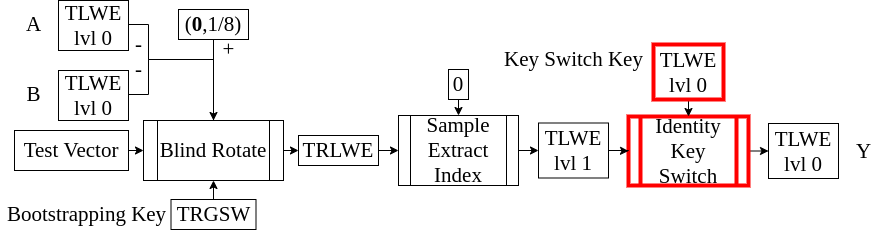
全体の中での位置づけ

Identity Key Switchingとは、恒等関数とKey Switchingを同時に適用する操作のことです。Key Switching自体は一般にはリプシッツ関数を同時に適用できるのですが、HomNANDでは恒等関数だけで問題ありません。

Key Switchingというのはその名前の通り、秘密鍵を変更する操作のことをいいます。ここでは、TLWEもちろん、秘密鍵で復号して再度暗号化するわけにはいかないので、暗号の上で復号関数に近いものを評価することになります。ここでは、TLWEからTLWEへのものだけを扱いますが、一般にはTLWEからTRLWE、TRLWEからTRLWEもあります。(これとか)

Key Switchingのアイデア

前回お話ししたBlind Rotateは非線形関数である符号関数を含む復号関数全体を評価していましたが、Key Switchingでは線形な部分だけ、つまり$b-\mathbf{a}\cdot\mathbf{s}$の部分だけを評価します。ノイズを除去するためには非線形関数である符号関数を適用する必要がありますから、Key Switchingではノイズは除去されず、ノイズは増加します。

Identity Key Switchingのアルゴリズム

ナイーブな実装

Identity Key Switchingの発想はExternal Productに近しいものです。実際、TRLWEからTRLWEの場合は自然にExternal Productを使って表現することができます。近い発想というのは具体的には、TorusとTorusの乗算は定義できないので、入力となるTLWEを整数に丸めて分解するという発想です。

ここではTLWElvl1からTLWElvl0への変換を考えるので、TLWElvl1の鍵($\mathbf{S}$)をTLWElvl0($\mathbf{s})$の暗号文として暗号化します。$b$の方は自明なTLWElvl0の暗号文として$(\mathbf{0},b)$と表現できます。なので、残りの$\mathbf{a}\cdot\mathbf{s}$を暗号文上で計算できればよく、つまりは$a_i\cdot s_i$をうまく計算できればそれらを全部足し合わせるわけでよいことになります。

Identity Key SwitchingにおいてExternal Productでの$Bg$に相当するパラメータが$base$で、$l$に相当するパラメータが$t$です。$base$は$Bg$と同様に実装では高速化のために$base=2^{basebit}$のように２冪にとります。

これらのアイデアだけを用いた場合、Identitiy Key Switchingのアルゴリズムはこのようになります。$KS_{ij}$は$\frac{S_i}{2^{j\cdot basebit}}$を暗号化したTLWElvl0の暗号文です。

b̃=b
for i from 0 to n
  ãᵢ = 0
prec_offset = 1 << (32 - (1 + basebit * t)) //四捨五入のため
for i from 0 to N-1
  āᵢ = aᵢ+prec_offset //四捨五入
  for j from 0 to t-1
    âᵢⱼ= ⌊baseʲ⋅āᵢ/2³²⌋ mod base
    (𝐚̃,b̃) -= âᵢⱼ ⋅ KSᵢⱼ
return (𝐚̃,b̃)

最適化された実装

ナイーブな実装にはまだ２つ最適化の余地があります。一つには、$base^j$倍して丸めるのを$base=2^{basebit}$の形であることを利用してbit演算に置き換えることができます。もう一つは、乗算の排除です。乗算をするとノイズがその分だけ大きくなってしまうため、$K_{ijk}=\frac{k\cdot S_i}{2^{j\cdot basebit}}$とし鍵へのアクセスで乗算を置きかえます。メモリ消費量は増えますが、ノイズの観点での改善はBlind Rotate側でのパラメータの調整の余地を増やすので全体としての高速化を実現できます。

これらを適用するとIdentitiy Key Swithingのアルゴリズムは以下のようになります。$k=0$のときは0との加算になるのでそもそもスキップできます。

IdentityKeSwitching((𝐚,b),𝐊𝐒)
  b̃=b
  for i from 0 to n-1
    ãᵢ = 0
  prec_offset = 1 << (32 - (1 + basebit * t)) //四捨五入のため
  for i from 0 to N-1
    āᵢ = aᵢ+prec_offset //四捨五入
    for j from 0 to t-1
      k = (āᵢ >> (32 - (j+1)⋅basebit))&(2ᵇᵃˢᵉᵇⁱᵗ - 1)
      if k != 0
        (𝐚̃,b̃) -= KSᵢⱼₖ
  return (𝐚̃,b̃)

次回

これでほとんどHomNANDに必要な説明は終わりで、次回でそれらをくっつけて終わりです。年末年始の休みに片付けてしまいたいけれど気分次第......