(完全)準同型暗号の最前線２（原理編）: TFHEの原理 #4 Blind Rotate

目次

1. (完全)準同型暗号の最前線1（入門編)
2. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #1 TLWE
3. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #2 TRLWE & SampleExtarctIndex
4. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #3 TRGSW & CMUX
5. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #4 Blind Rotate←イマココ
6. (完全)準同型暗号の最前線２（原理編）: TFHEの原理 #5 Identity Key Switching

初めに

セキュキャンも近いので講義の下書き的なノリで書き進めなきゃなぁの勢いで書ききっています。つまり、わかりにくいなと思ったらまた修正するかも.......
Blind Rotateは私の理解度が上がったがゆえに説明するのが逆に説明するのが難しくなった(一般性を余り損ないたくない)という感じがあって難しいところです。
読む側としては個人的にはExternal Productの次に難しいのかなと思っています。

全体の中での位置づけ

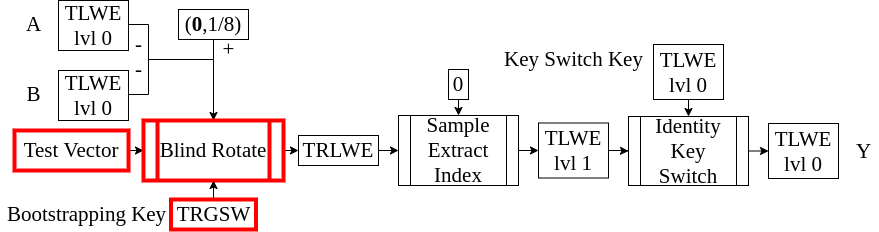
Blind Rotateは入力となるTest Vector(一般にはTRLWEであるが、平文の多項式も自明な暗号文としてTRLWEにできるのでそれを刺す場合も在る)を入力となるTLWEに応じて「回転」させる操作のことです。
ここでいう「回転」というのは、$X$のべき乗を書けるということで、詳しくは次の節で説明します。
Blind RotateはTFHEにおいて根幹となる操作ですが、それはTLWEの値に応じて多項式の係数を在る特定の位置に持ってこれるならば、その係数を抜き出す(これはSample Extract Indexによってできます)ことで多項式の係数をテーブルとしたLook Up Tableを評価できるということになるからです。(あくまで意図を説明しているだけで、もちろんこの時点でこの文の意味を理解する必要はありません)
HomNANDの構成では、復号の際に使う符号関数という非線形関数を評価するためにこの仕組みを使います。

「回転」の意味

「回転」というのは先に述べたように$X$のべき乗を書けることなのですが、これは考える対象が$X^N+1$を法とした多項式環の上のものを考えているからです。
$\mathbb{T}_N[X]∋p[X]=∑_{i=0}^{N-1}p_iX^i$とすると、以下のような性質が成り立ちます。
$$X⋅p[X]≡-p_{N-1}+∑_{i=0}^{N-2}p_iX^{i+1} \bmod X^N+1$$
これは$X$倍すると最高次の係数が最低次へと「符号を負にかえて巡回」してくることを示しています。このような性質を一般に負巡回といいます。
上の性質から明らかに演繹されることとして、以下のような性質があります。
$$X^{N}⋅p[X]≡-p[X] \bmod X^N+1,X^{2N}⋅p[X]≡p[X] \bmod X^N+1$$
つまり、$X^N$を掛けると全ての係数の符号が負になったものが得られ、$X^{2N}$を掛けると元に戻ります。
更にこの性質から、$f,g\in\mathbb{Z}$に対して以下のような性質も成り立つことは自明でしょう。
$$X^f⋅X^g⋅p[X] ≡ X^{f+g \bmod 2N}⋅p[X] \bmod X^N+1$$
Blind Rotateではこれらの性質を基本的な構成要素として用いています。

Blind Rotateでやろうとしていること

先に述べた「TLWEの値に応じて多項式の係数を在る特定の位置に持ってこれるならば、その係数を抜き出すことで多項式の係数をテーブルとしたLook Up Tableを評価できる」という言葉をもう少し正確に説明しましょう。
今入力となるTest Vector(TRLWE)を$TV[X]$、TLWEを$(\mathbf{a},b)$のように書くとし、$\rho = \lceil 2N\cdot b\rfloor - \sum_{i=0}^{n-1} \lceil 2N \cdot a_i \cdot s_i\rfloor \bmod{2N}$(ここでの掛け算はTorusを一時的に実数とみなしていることに注意)とします。
Blind Rotateは以下の式を暗号文のまま評価する操作です。

$$X^{-\rho}\cdot TV[X]$$

定義から明らかなように、$\rho\approx 2N\cdot(b-\mathbf{a}\cdot\mathbf{s})$です。
$b-\mathbf{a}\cdot\mathbf{s}$を丸めると平文になるわけであるから、$\rho$は概ねTLWEの平文に対応していると考えて良いでしょう。
つまり、「Blind Rotateは入力となるTLWEの平文に応じた量だけTest Vectorを回転させる操作」ということになります。
#2 TRLWE & SampleExtarctIndexで既にSample Extract Indexを説明していますが、これを使うとTRLWEの特定の係数を抜き出したTLWEを作ることが出来ます。
これを常に回転後のTRLWEの定数項(一般には固定の位置ならどこでもいいのですが)を抜き出すように適用するとすると、回転後の定数項が回転前のTRLWEの何次の項で符号の正負がどちらか、というのは入力するTLWEに依存します。
つまり、「Blind Rotateは入力となるTLWEの平文に応じた次数・符号のTest Vectorの係数を定数項に持ってくる」操作とみなせば、「Blind Rotateと定数項へのSample Extract Indexの組み合わせは、TLWEをIndexとしてLook Up Tableを引く操作」と言えます。
そしてLook Up Tableのindexと値の対応はTest Vectorで決まるわけです。
指数が$\rho$ではなく$-\rho$になっているのもこのLook Up Tableのことを念頭に置いているからです。
$X^{-\rho}$にすれば、$\rho\in[0,N)$ならTest Vecotorの$\rho$次の係数が定数項に来て、$\rho\in[-N,0)$なら$N+\rho$次の係数の符号を反転させたものが定数項に来ます。つまり、$\rho$の符号と定数項に来る係数の符号が対応します。

符号関数を評価するためのTest Vector

$\rho$が正符号なら$\frac{1}{8}$が、負符号なら$-\frac{1}{8}$が定数項に来ればよいので、$(0,\sum_{i=0}^{N-1}\frac{1}{8}X^i)$をTest Vectorとして用いれば符号関数が評価できます。
このようにTLWEにせよTRLWEにせよ$a$の方を$0$にしたものは秘密鍵の情報も乱数生生成器へのアクセスもなしに生成できる有効な暗号文(もちろん平文を秘匿する能力はないが)であるので、自明な暗号文といいます。

Blind Rotateのアルゴリズム

ここでは$X^{-\rho}\cdot TV[X]$を実際にどうやって評価するかについて述べます。
$\rho$の値がもしわかってしまったら、それは平文が漏洩することになりますから、当然出来ません。
$\rho$を暗号文として先に計算するというアプローチだと、TLWEでもTRLWEでもTRGSWでも$X$の肩に載せるということが出来ません。
TFHEでは、$X$の肩に載った状態で$\rho$を計算することでこれを解決します。
まず思い返すべきは、指数の足し算は乗算に置き換えれるということです。($\prod$は総乗記号です)

$$X^{-\rho} \equiv X^{-\lceil 2N\cdot b\rfloor}\cdot\prod_{i=0}^{n-1}X^{\lceil 2N \cdot a_i \cdot s_i\rfloor} \bmod{X^{N+1}}$$

$X^{-\lceil 2N\cdot b\rfloor}$は暗号文がわかっていれば計算できるので問題ないです。しかし、秘密鍵$\mathbf{s}$はわかりませんから、$X^{\lceil 2N \cdot a_i \cdot s_i\rfloor}$をどうやって計算するのか、というのがBlind Rotateの構成では根幹となります。
一般には指数の上での乗算はべき乗に置き換えることが出来ますが、$s_i$がわからないのでべき乗は計算できません。
この問題を解決するのに重要なことは、$\mathbf{s}\in\mathbf{B}^n$であることです。
これは、$X^{a_i \cdot s_i} = s_i?X^{a_i}:1$を意味します。(s?d1:d0はC言語などで見られる３項演算子で、sがtrueならd1、falseならd0が返ります)
つまり、べき乗をする代わりに$s_i$を制御入力、$X^{a_i},1$をデータ入力としたマルチプレクサに置き換えることができるわけです。
すでに#3 TRGSW & CMUXでCMUXを導入していますから、このマルチプレクサをCMUXで評価する、というのがTFHEにおけるBlind Rotateの重要な点です。
これを実現するには$s_i$をTRGSWで暗号化したものが必要になります。これを特別にBootstrapping Keyと呼びます。名前の理由は最後に説明します。
ここまでで概ねの説明は出来ていますが、もうひとひねり加えます。TRLWEとTRLWEの積は定義していないので、$X^{a_i \cdot s_i}$をCMUXで計算してからTRLWEを掛け合わせるというわけには行きません。
そこで、$0\leq k< n-1$について成り立つ以下の漸化式を計算するようにします。

$$X^{-\lceil 2N\cdot b\rfloor}\cdot\prod_{i=0}^{k+1}X^{\lceil 2N \cdot a_i \cdot s_i\rfloor} \equiv \left[s_{k+1}?X^{\lceil 2N \cdot a_{k+1}\rfloor} \left(X^{-\lceil 2N\cdot b\rfloor}\cdot\prod_{i=0}^{k}X^{\lceil 2N \cdot a_i \cdot s_i\rfloor}\right):X^{-\lceil 2N\cdot b\rfloor}\cdot\prod_{i=0}^{k}X^{\lceil 2N \cdot a_i \cdot s_i\rfloor}\right] \bmod{X^{N+1}}$$

この漸化式では、$X^{-\lceil 2N\cdot b\rfloor}\cdot\prod_{i=0}^{k}X^{\lceil 2N \cdot a_i \cdot s_i\rfloor}$はTRLWEで保持されますが、$X^{\lceil 2N \cdot a_{k+1}\rfloor}$はTLWEの係数の１つから直接計算できるので平文であり、TRLWE同士の乗算を避けることが出来ます。
このように指数の上の計算を漸化式として表現することで暗号文同士の乗算を避ける方法はcryptographic accumulatorと呼ぶことがあります。
ここまで来たら後はBlind Rotateの式を実際にアルゴリズムにおこせばよいでしょう。

BlindRotaete((𝐚,b):TLWElvl0,𝐁𝐊:Bootstrapping Key, TV[X]: Test Vector)
  b̃=((b + (1<<(31-Nbit-1)) ) >> (32-Nbit-1))//足し算は四捨五入をするため
  trlwe = X⁻ᵇ̃⋅TV[X]
  for i from 0 to n-1
    ã=(aᵢ + (1<<(31-Nbit-1)) ) >> (32-Nbit-1)
    trlwe = CMUX(𝐁𝐊ᵢ,Xᵃ̃⋅trlwe,trlwe) //Dec(𝐁𝐊ᵢ)?Xᵃ̃⋅trlwe:trlwe
  return trlwe

なぜBootstrapping Keyというのか

まず第一に、Bootstrapping Keyは秘密鍵が同じなら同じものを何度も使いまわすことが出来ます。それに加え、秘密鍵に関する情報を直接的に持っています。それらの意味で、これはKeyだということが出来ます。
HomNANDの符号関数の評価では$(0,\sum_{i=0}^{N-1}\frac{1}{8})$というノイズを含まない自明な暗号文をTest Vectorとして用いており、$X^{\lceil 2N \cdot a_{k+1}\rfloor}$などは暗号文から直接計算され、かつこれをTRLWEにかけるだけではノイズは増えません。
つまり、Blind Rotateの出力となるTRLWEのノイズはCMUXだけで増加する。しかも、CMUXでのノイズの増加量はBootstrapping Keyだけに依存する。つまり、Blind Rotateの出力となるTRLWEは入力となるTLWEのノイズには寄らないのである。
これはこのBlind RotateこそがTFHEにおけるBootstrapping、つまりノイズのリフレッシュそのものとなっています。他の操作は厳密には入出力の形式を整えているだけです。
というわけで、名前通り、Bootstrappingに使うKeyだからBootstraping Keyとよんでいるわけです。

GateBootstrappingTLWE2TLWE

Blind RotateとSample Extract Indexを組み合わせて符号関数を評価する操作にはGateBootstrappingTLWE2TLWEという名前がついています。以下にアルゴリズムを書き下しておきましょう。
注意するべきことは、入力のTLWEはlvl0ですが、出力はlvl1であることです。ですので、HomNANDへの入力と出力で暗号文の形式を揃えるためには、次回説明するIdentity Key Switchingが必要です。

GateBootstrappingTLWEtoTLWE((𝐚,b):TLWElvl0,𝐁𝐊:Bootstrapping Key)
  testvec = (0,0)
  for i from 0 to N-1
    testvec += (0,1/8⋅Xⁱ)
  trlwe = BlindRotate((𝐚,b),𝐁𝐊,testvec)
  return SampleExtractIndex(trlwe,0)

次回

Identity Key Switchingを説明します。Blind Rotateよりは簡単でしょう。いつ書き上がるかはよくわかりません()