目次
- (完全)準同型暗号の最前線1(入門編)
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #1 TLWE←イマココ
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #2 TRLWE & SampleExtarctIndex
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #3 TRGSW & CMUX
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #4 Blind Rotate
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #5 Identity Key Switching
- (完全)準同型暗号の最前線2(原理編): TFHEの原理 #6 HomNAND
初めに
この記事は(完全)準同型暗号の最前線1(入門編)の続きです。
単体でも意味をなすとは思いますが。
やっぱ講義の簡易日本語テキスト版ということでTFHEについて書こうと思います。
TFHEは完全準同型暗号にしては構成がきれい(個人の感想です)ですが、それでも説明しようとすると大変なので6つに分けます。
基本的にはセキュリティキャンプの講義資料で喋っていたことを文字に書き起こしたものですが、Introductionが入門編に、Parameter Selectionは理論編に吸収されたということになりますね。書くのが面倒だから詳細を飛ばすとか逆にいい忘れてたことを書いてるとかそういうことは普通にあると思います。また、セキュリティキャンプは性質上実装に重きをおいていましたが、ここでは説明の量を減らすためにもっと抽象度の高い数式のレベルでの説明にとどめます。
目標
この記事を含む原理編では第3世代FHEの一つであるTFHEの原理を、NAND演算を暗号のまま行うのに必要最低限な範囲で説明します。
全体像
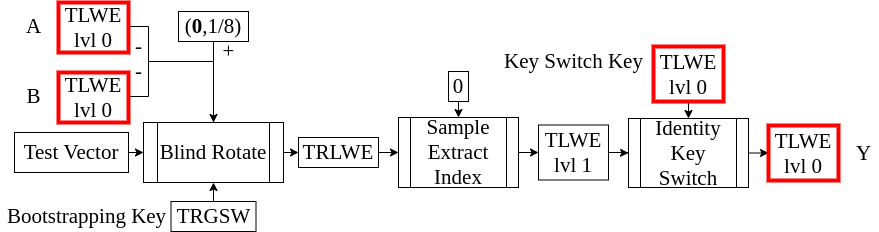
NAND演算を暗号のまま行う関数(HomNAND)の全体像はこんな感じでこの記事では赤くなっているTLWElvl0について説明します。(TLWElvl1の説明もしているとは言えるのですがTRLWEのとこで説明しているということにしたほうがきれいなので)
Torusとは
日本語でいうと、 円周群のこと。ここでは定義として、$\mathbb{T}:=\mathbb{R}/\mathbb{Z}$を採用する。つまり、実数の小数部分の集合である。
注意すべき特徴としては、Torus同士の加法は定義できるが乗算は定義できず、しかし整数とTorusの乗算は定義できるということである。
Torusを時計の針の角度のようなものだと思えば直感的にわかるかもしれない。(角度かける角度は定義できないか角度ではないなにかである)時計の針のイメージでは角度をラジアンで表記したものを$2\pi$で割ったものを考えればこれが$\mathbb{T}$と全く同じものであることがわかるだろう。
- 加算の例: $0.8+0.6=1.4≡0.4 \bmod 1,0.3-0.9=-0.6 ≡ 0.4 \bmod 1$
- Torus同士の乗算が定義できないことの例: $1.2≡0.2 \bmod 1,2.4≡0.4 \bmod 1$なので、乗算が定義できるなら$1.2⋅ 2.4=2.88≡0.2⋅0.4=0.08\bmod 1$だが成立しない。
- 整数($\mathbb{Z}$)との乗算は定義できることの例: $3⋅ 0.4≡ 0.2 \bmod 1$
TLWEとは
Torus Learning With Errorの略で、格子暗号の一種であるLWEのTorus版、という意味。LWEがどういう暗号なのかというのは理論編でしゃべるので、ここでは暗号のデータ形式、暗号化と復号の手順だけを示します。安全性の評価については後から学んでも十分であるためです。
ちなみに現在使われているLWEはよくすべての要素が剰余環上の整数ということになっていますが、元々のLWEはWikipediaみてもわかるとおりTorusを含んでいるのでその意味ではそこまで変な亜種ではないです。
また実際の実装では固定小数点表記でTorusを表すので実質的にTorusは剰余環上の整数として扱われます。
モジュラー正規分布
TLWEはLWEの一種なので、ノイズ(Errorなんだから誤差のほうがいいのかもしれませんが)を生成する必要があります。TLWEではそのノイズの生成源として(それ以外の選択肢はありえますが一番簡単な構成として)モジュラー正規分布(Modular Gaussian Distribution)を用います。その名の通り、正規分布に少し手を加えたもので、正規分布からとったサンプルを$\bmod 1$したものです。つまり、正規分布からとったサンプルは実数ですが、それを自然にTorusに写しただけのものです。
記法として、$\mathcal{D}_{\mathbb{T},α}$を平均$0$標準偏差$α$のガウス分布を$\bmod 1$したモジュラー正規分布とします。
TLWEの具体的構成(平文がTorusな場合)
$\mathbb{B}={0,1}⊂ \mathbb{Z}$で、バイナリの値の集合。暗号の安全性を決めるパラメータは2つで$n∈\mathbb{Z}^+,α∈\mathbb{R}^+$。 $U_{\mathbb{T}^n}$を$\mathbb{T}$から$n$個の値を独立にとる一様分布とする。
$\mathbf{a}∈ \mathbb{T}^n, e,b∈ \mathbb{T}, \mathbf{s}∈ \mathbb{B}^n,m∈ \mathbb{T}$とする。$m$を平文、$\mathbf{a}←U_{\mathbb{T}^n}$,$e←$$\mathcal{D}_{\mathbb{T},α}$,$\mathbf{s}←U_{\mathbb{B}^n}$とする。$←$は確率分布からサンプルを取ることを示している。
そうすると、TLWEの暗号文は$b=\mathbf{a}⋅ \mathbf{s}+ m +e$として、$(\mathbf{a},b)$というn+1要素のベクトルとして書くことができる。つまりこれが暗号化の関数でもある。
$b-\mathbf{a}⋅\mathbf{s}=m+e$になるので、この$e$をどうにかして削除する方法(これは平文空間をTorusより制限しないと通常定義できないので今はおいておく)を加えると$m$がとれて復号できる。
$b-\mathbf{a}⋅\mathbf{s}$はphaseと呼ぶこともあります。(Torusの角度に相当するからだと思います。)
$n,α$を大きくすればするほど安全($α$は大きくしすぎると暗号文が壊れる)であるがどうしてそうなるのかは理論編で。
TLWEの加法準同型性
入門編でも行ったとおり、格子暗号はそのままでもPHEになっています。ここでは実際にTLWEが加法準同型性を満たしていることを確認しておきましょう。
2つの暗号文$(\mathbf{a}_1,b_1),(\mathbf{a}_2,b_2)$を考え、その(準同型演算としての)和を$(\mathbf{a}_1+\mathbf{a}_2,b_1+b_2)$とします。
$b_1+b_2-(\mathbf{a}_1+\mathbf{a}_2)⋅\mathbf{s}=m_1+m_2+e_1+e_2$になり、$m_1+m_2$が出てくるので加法準同型になっていることが分かります。
ノイズが大きすぎるとノイズを取り除ききれなくて復号を誤る確率が大きく(復号を誤る確率があるというのがLWEの特徴の一つです)なりますが、足し算をするとノイズも$e_1+e_2$となって大きくなっているので、足し算ができる回数には限界があります。
代数構造をベースとしているPaillierとかだとノイズという概念はないので加算回数には制限がなく、その点には留意しておく必要があります。
TLWEの具体的構成(平文がバイナリな場合)
さっきの定義とほぼ同じまま、$m∈ \mathbb{B},μ=1/8\in\mathbb{T}$と置き直します。$μ(2⋅ m-1)∈\mathbb{T}$です。($\mu$はどっから来たのかというのは最後(6番目)に説明しても支障ないのでとりあえず置いときますが意味はあります。)
そうすると平文空間がバイナリの場合は($m$を$μ(2⋅ m-1)$に置き換えて)TLWEの暗号文は$b=\mathbf{a}⋅ \mathbf{s}+μ(2⋅ m-1)+e$になります。
復号は$(1+\mathit{sgn}(b-\mathbf{a}\cdot\mathbf{s}))/2$になります。($\mathit{sgn}$は符号関数)
復号のときには$\mathbb{T}=[-0.5,0.5)$という符号付きの空間になっていることを仮定しています。($\mathbb{T}=[0,1)$としたほうが都合の良い場合もあって、実装では適宜変えたりもしますがこの一連の記事では$\mathbb{T}=[-0.5,0.5)$だけでいいはずです)$\mathit{sgn}$がノイズを取り除く関数になっているわけです。$e$が大きすぎると、本来負になるべきところが正になってしまったりその逆もあるので復号を誤ることがあるわけです。
次回
次回はTRLWEの話ですね。まぁそれはいいんですけどその次のTRGSWの説明がどうしたものか......