筆者について
大阪の大学院生です。教師あり学習にずっぽり触れてきましたが、最近強化学習、特にマルチエージェントの話について興味をもって、いろいろ弄っています。まだまだ未熟者なので、玄人の方はお手柔らかにお願いします。
概要
マルチエージェント学習、つまり複数の個体が対象である分散型システムについての強化学習において、分散型部分観測マルコフ仮定(Decentralized POMDPs)というものがあります。
論文はこちら。
分散型システムを考える場合、上記のように学習対象は一部のデータしか観測できない状況で、かつ各々が学習領域を持っていることが多いです。これは例えば衛星などを考えた際、搭載されたセンサーから得られるデータに限界があるように、実問題で各々のエージェントが観測できるデータに制限があることが背景の一つとしてあると考えられますね。
Decentralized-POMDPs は以下のように記述されます。
(S, (A_i), T, R, (Ω_i), O, γ)
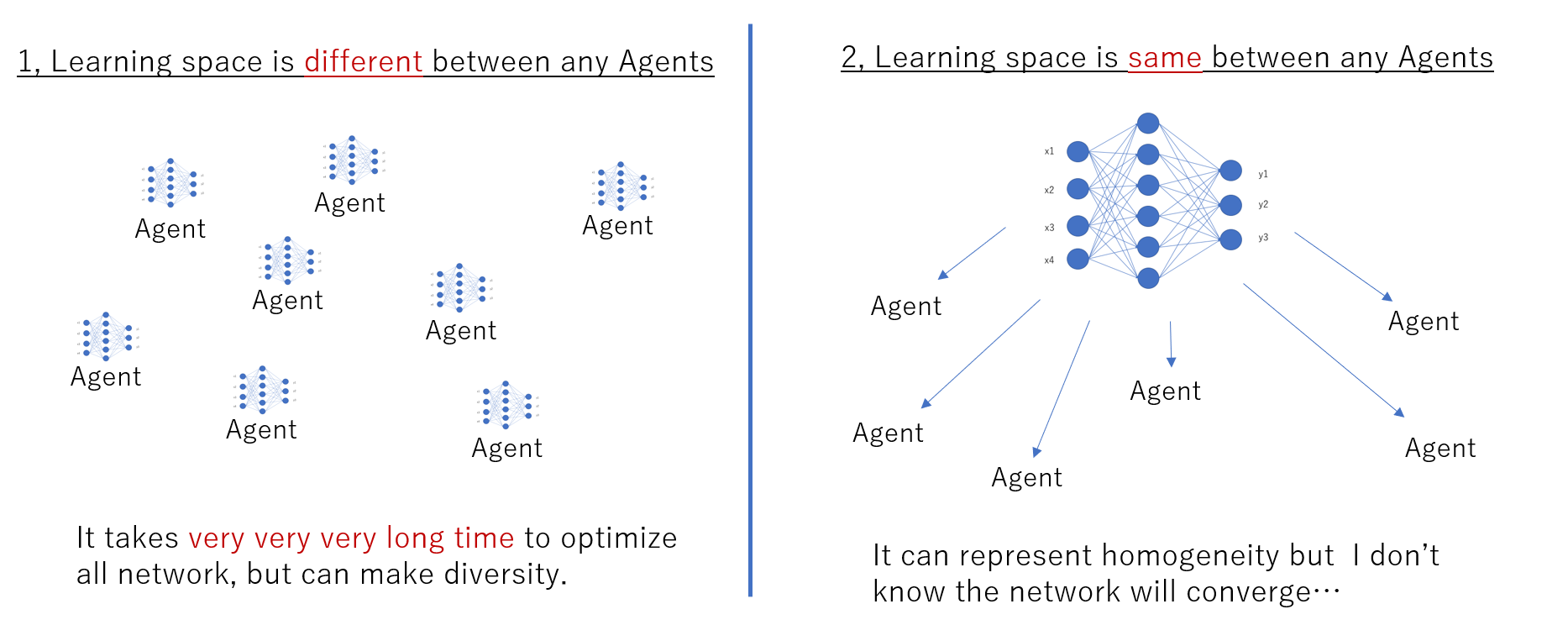
今回は、部分観測ではなく全体観測が可能で、かつ各々のエージェントが同じ学習領域を持ったモデルを考えたいと思います。
マルコフモデルは以下のようになります(多分)。
(S, (A_i), T, R, Ω, O, γ)
つまるところ、観測の集合を統一したものですね。Decentralized-POMDPsのほうが一般化されているので、内包されている条件とも捉えられます。
今回はこれのもっとも簡単な問題について、実験することにしました。
前提
そもそもの強化学習については、以下の書籍をお勧めします。収束などわかりやすく書いていて良いです。確率統計を学んでからのほうが良いと思いますが、、、
強化学習モデルは、DQNを使うことにしました。これはいろんな方々が分かりやすく説明されているので論文よりもそっちを見るほうが早いですね。一応参考程度に。
まあ最も、今回の記事は初学者はかなり置いてけぼりだと思いますすみません、、、
理論
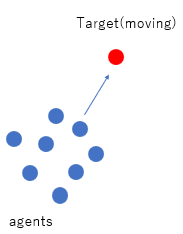
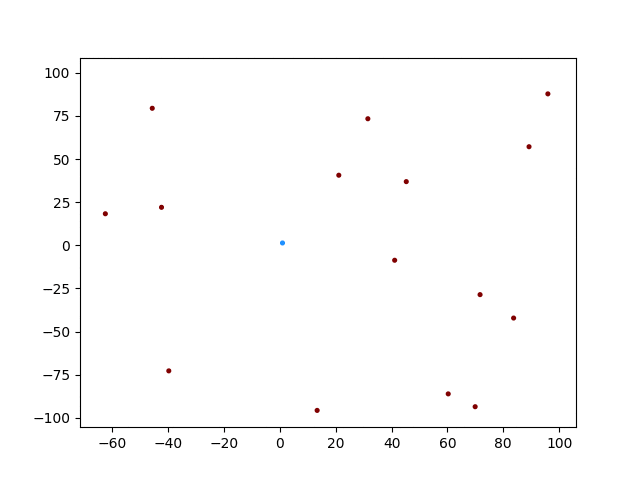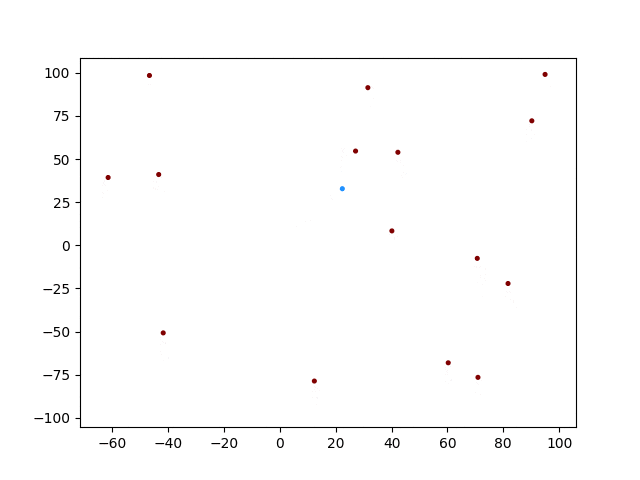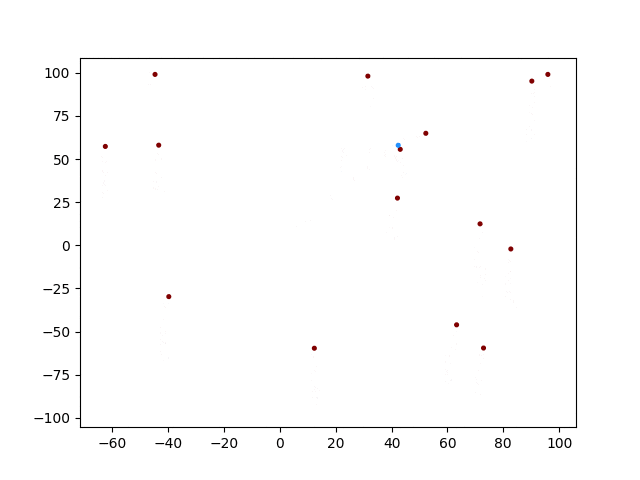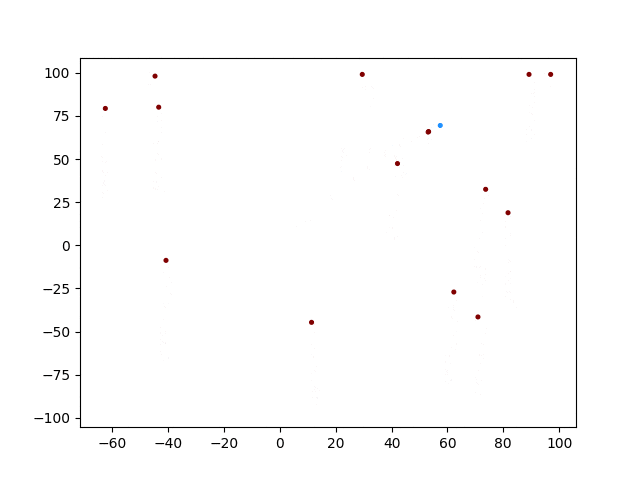
さて、今回は追跡問題を解いてみます。と言っても、逃げるほうは一定の軌道を描き、たくさんの鬼が追いかけるというものです。以下のように、青のエージェントを学習させます。
また以下のように学習空間が一つなので、以下の図の右側のように計算コストはエージェントの数に依存せず一つとなります。ただ、この計算が収束するかどうかは微妙ですが、、、
状態関数
deep Q-Lerningなので、状態関数は連続地でも大丈夫です。しかしネットワークの特徴として、入力ベクトルの次元が一定でなければなりません。これは 参考文献1 でも取り上げられている通り、部分観測をした場合の問題点になり得ますね。今回は異なりますが、部分観測でも取り合扱えるよう、状態関数は場の理論を用いた、一般化した方法を考えることにしました。
部分観測でよく使用されるのはグラフ理論です。観測条件を記述できるからですね。条件によって観測ベクトルが変化しないよう、状態を場でとらえて、ネットワークに入力することにします。イメージは以下の通りです。
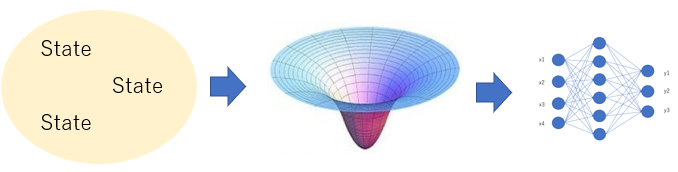
今回の問題では、上の図におけるStateは他のエージェントjの距離ベクトル、そしてTargetとの距離ベクトルとします。それを用いて、以下の数式を立てました。ここで、S1,S2,S3,S4がネットワークに代入する値です。
S1=𝑥_𝑖−𝑥_{𝑡𝑎𝑟𝑔𝑒𝑡}
S2=𝑦_𝑖−𝑦_{𝑡𝑎𝑟𝑔𝑒𝑡}
𝑆3= \frac{𝜕}{𝜕𝑥}\Bigg(\sum_{j}\frac{𝑎}{\sqrt{(x-x_j)^2+(y-y_j)^2}}\Bigg)| 𝑥=𝑥_𝑖
𝑆4= \frac{𝜕}{𝜕y}\Bigg(\sum_{j}\frac{𝑎}{\sqrt{(x-x_j)^2+(y-y_j)^2}}\Bigg)| y=y_𝑖
S3,S4については、電荷などのポテンシャルエネルギーを参考にしています。距離が近くなるほど値が大きくなり、付近に他の個体の存在を表すことができます。
これによって、もし部分観測で毎度毎度観測できる個体の数が変化してもネットワークに代入する数は同じになりますね。最も今回は全部観測してもらうので関係ないですが()
報酬関数
一応Targetとの距離が近いほどよいものを考えたいので、
R_i=-|r_i-r_{target}|
は取り入れます。また、集団の形をきれいにしたい思惑があるので、一定の距離を保ってもらうよう各々の距離に対する分散と平均にもとに、以下も考えることにしました。なおこれはある時刻においてすべてのエージェントが共通して得られる報酬なので、R_swarm と書くことにします。
R_{swarm}=-(average(p_i)+variance(p_i))
p_i=min(r_i-r_j)
わかりやすく言えば、みんな一番近い個体との距離は一緒にしようねという感じです。
最後に、衝突があった場合は罰則を与え、これをR_crash-iとします。
以上をもって、報酬関数は
R_i'=R_i+R_{swarm}+R_{crash-i}
とします。
ポイント
Target, Egent含め、衝突が発生しないようにします。なので、最終的にお互いが距離を取り合いながらTargetを追いかける集団ができそうです。
また、衝突が起きた際に計算を終了させています。
実装and結果
コードは以下に乗せておきます。
(とはいえかなり雑多で多分コメントとかも何もないので参考にはならないと思います、、、)
できない!!(笑)
青色がTrgetですが、近くに来た奴は恐る恐る近づいていますね。そして衝突したところで計算が終わっています。しかし他の個体は同じような動きをしていますね。おそらくネットワークを共有しているので、領域内での学習が全く収束していないと思いますが、、、どうなんでしょうか。考察と改変の余地はたくさんありそうです。
終わりに
別に論文に書くほどのことでもないけど面白そうなのでやってみました。欲しい結果が得られなかったことは残念ですが、分散システムについてもっと勉強したいと思います。
参考資料(論文)
実装環境
Docker for windowsでpytorchを内包したUbuntu環境をpullして利用しました。dockerは他の方が構築してくれた環境を利用できるので便利ですね。