総研大 統計科学コースの平元です。アドベントカレンダーを書くことになったのでデータ同化普及のための記事を書きます。
粒子フィルタを実装するときのプログラミング言語 小規模モデル編
前回の記事(リンク)では、データ同化の基本的な考え方と、カルマンフィルタ/アンサンブルカルマンフィルタ/粒子フィルタといった代表的な手法の違いを紹介しました。
しかし実際に現場で問題になるのは推定精度だけではなく、計算時間です。
とくに数値天気予報・気候モデル・海洋モデルのような大規模シミュレーションでは、
- 高解像度の全球モデルで推定する
- 数十〜数百メンバーのアンサンブルを長期間回す
といった理由から、スパコンを何日も(場合によっては 1 週間以上)回し続ける ような計算が当たり前に行われています。一方で、ロボティクスやリアルタイム制御の分野では、搭載できるハードウェアに強い制約があるため、 「どれだけ軽く・速く動かせるか」 が非常に重要になります。
理論面での工夫としては、たとえば Rao–Blackwellized Particle Filter(RBPF)のように「条件付きで解析解を使える部分はカルマンフィルタに押し込めてしまう」ことで、計算量と分散を同時に減らす方法も知られていますが、これについてはまた別の記事で触れたいと思います。
今回はもっと素朴に、
- 同じ粒子フィルタを Python / Rust / Julia / Fortran の 4 言語で実装して、実行時間を比べてみる
という小規模ベンチマークを行った結果を紹介します。
なお、ここで扱うのはごく小規模な 1 次元時系列モデルです。そのため、
- 「この結果そのままが、大規模モデル(Lorenz-96 や全球 NWP モデルなど)でも成り立つ」
とまでは言えません。大規模モデルと結果が異なる大きな要因の一つとしては並列化の工夫で、小規模モデルでは並列化によるメリットよりもオーバーヘッドのデメリットのほうが大きいため、小規模・大規模モデルで使える技術が変わるためです。
また実装によっても変わるため、今回の結果は傾向としての参考値くらいに見ていただければ幸いです(大規模モデル編もそのうちやります)。
使用データ
前回の記事と同じく、ここでは 3 種類の 1 次元状態空間モデルを使います。
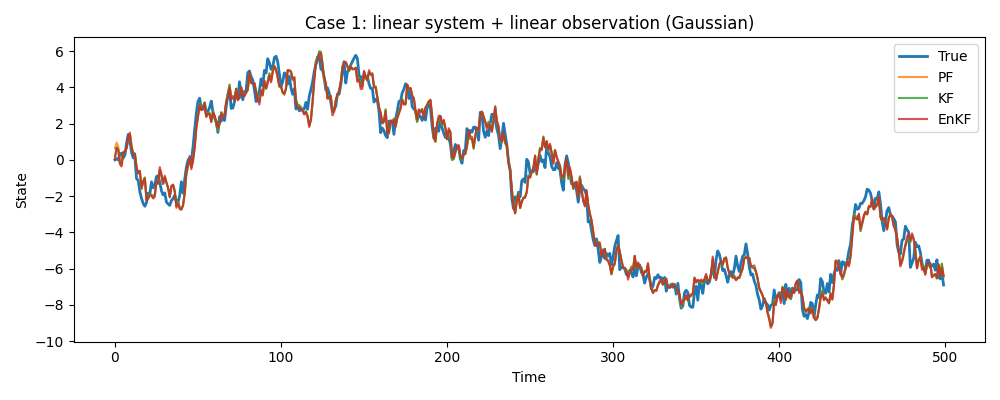
- データ①:完全に線形・ガウス(カルマンフィルタの教科書的ケース)
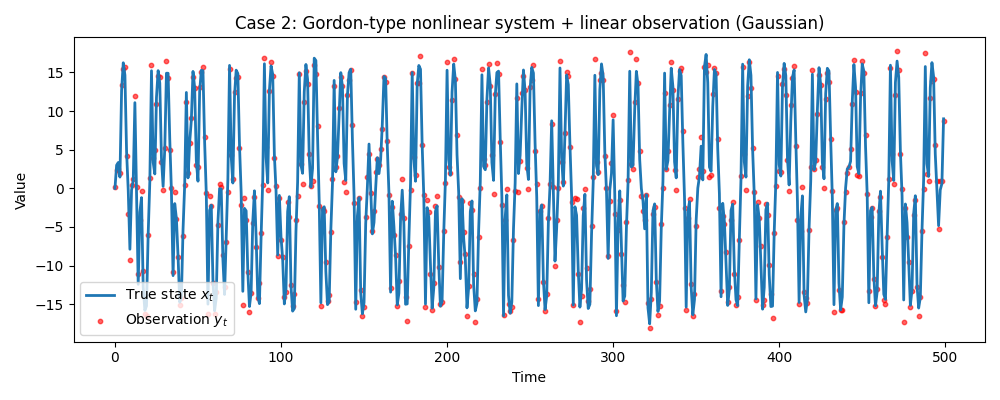
- データ②:非線形システム・ガウスノイズ(Gordon et al. 1993 の古典的ベンチマーク)
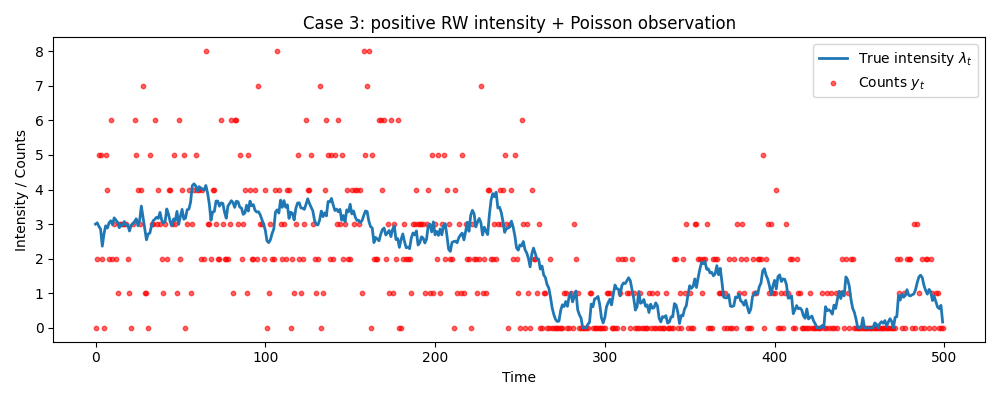
- データ③:非線形・非ガウス(状態は連続、観測は Poisson カウント)
いずれも
- 潜在状態 $x_t$(あるいは $\lambda_t$)
- 観測値 $y_t$
を持つ状態空間モデルで、システムノイズ・観測ノイズの性質を少しずつ変えています。
データの規模はいずれも「1 次元 × 数百〜数千時点」程度の、ごく小さなものです。
以下のサブセクションは前回の記事からの引用ですが、今回の記事だけ読んでも意味が通るよう、見出しと簡単な説明を付け直しています。
データ① 線形・ガウス
単純なランダムウォーク。状態の変化も、観測される値もすべて線形かつノイズが正規分布です。
データ② 非線形システム・ガウス
システムモデルに非線形関数(Gordon et al. 1993 のベンチマークモデル)を使用します。
ノイズは正規分布に従うものの、状態の更新式が非線形です。
$$
x_t = 0.5 x_{t-1} + \frac{25 x_{t-1}}{1 + x_{t-1}^2} + 8 \cos(1.2t) + v_t
$$
式がかなり複雑なため、通常の KF を無理やり適用すると線形化誤差が大きくなります。
EnKF(アンサンブルカルマンフィルタ)は、粒子(アンサンブル)を使ってこの複雑な形状をシミュレーションしつつ、「分布がほぼガウス」という仮定を利用することで、PF より少ない計算量でそこそこ現実的な解を出すことができます。
データ③ 非線形・非ガウス
最後は明確に非ガウスなケースです。
マーケティングデータや来客数のように、「0 以上の整数(カウントデータ)」のみが観測される状況を想定し、Poisson 観測モデルを用います。
$$
\begin{aligned}
\lambda_t &= \max(\lambda_{t-1} + v_t,\ \varepsilon),\
v_t &\sim N(0, \sigma_v^2),\ \varepsilon > 0
\end{aligned}
$$
$$
y_t = \mathrm{Poisson}(\lambda_t)
$$
- $\lambda_t$:観測カウントの期待値(強度)
- $y_t$:実際に観測されるカウントデータ
$\lambda_t$ が負にならないように $\max(\cdot,\varepsilon)$ をとっているため、システムモデル自体も非線形です。
観測は $\lambda_t$ を期待値とした Poisson サンプリングであり、離散かつ非対称な非ガウス分布になります。
実験設定
推定手法はすべて標準的なブートストラップ粒子フィルタ(予測 → 重み計算 → リサンプリングの繰り返し)とし、粒子数は 10,000 固定としました。
- 3 ケース(線形ガウス / Gordon 非線形ガウス / Poisson カウント)
- 各ケースについて 4 言語(Python / Julia / Rust / Fortran)で同じモデルを実装
- 各実装を複数回実行し、
- 推定精度:真値との RMSE
- 実行時間:平均秒数
time_mean_secと標準偏差time_std_sec
を計測しています。
粒子フィルタの理論やアルゴリズムの詳細については、たとえば以下の教科書が非常にわかりやすいです:
実際のコードは GitHub にあるので、実装レベルの細部に興味がある方はそちらを参照してください。
推定結果
- RMSE の値はどの言語でもほぼ一致しており、実装の違いによるバグはなさそう
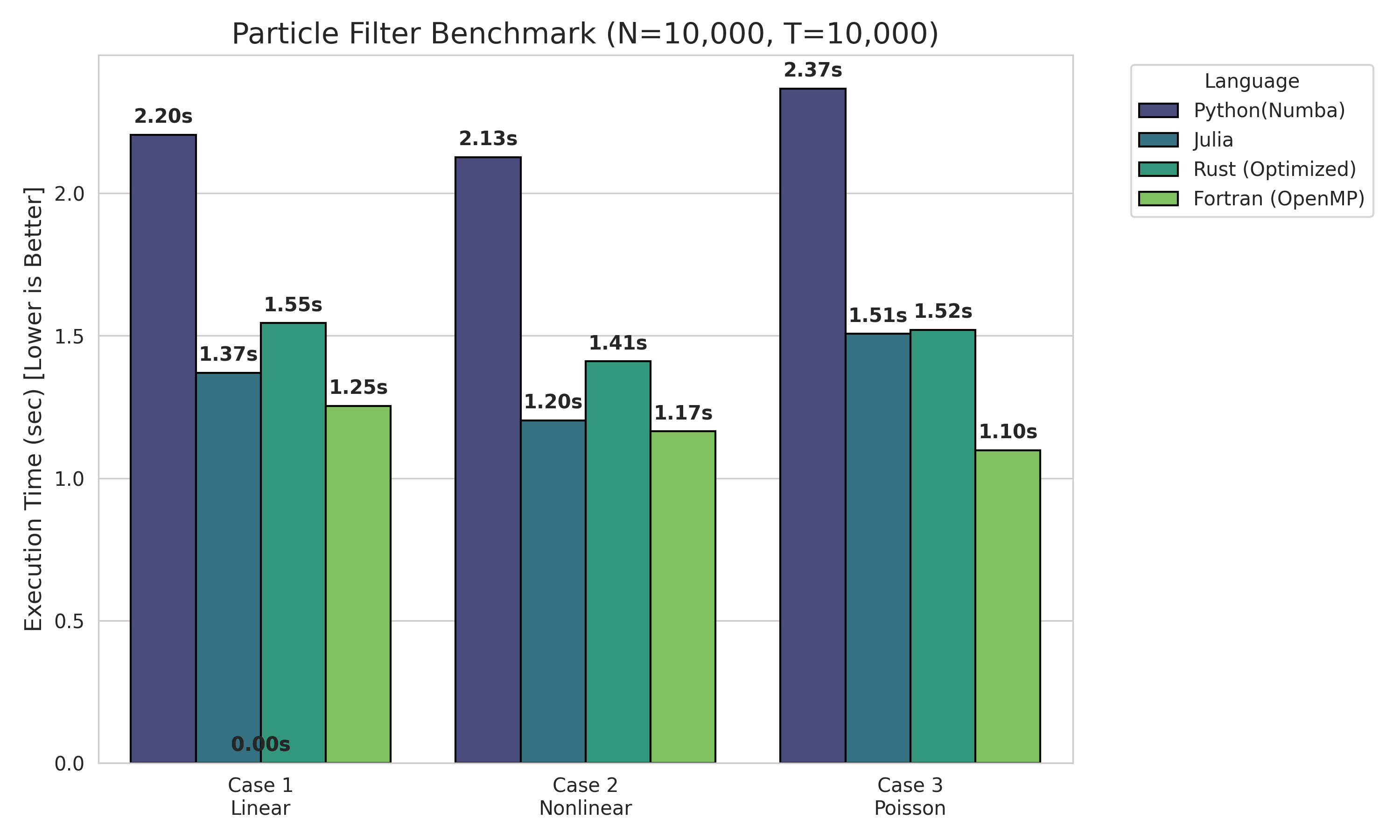
- 実行時間については、今回の設定では
Fortran ≥ Julia ≳ Rust > Python(Numba)
という傾向になりました。
計測した結果を表にまとめると、次のようになります。
Case1 : 線形・ガウス
| language | #particles | RMSE | mean time [s] | std [s] |
|---|---|---|---|---|
| Python | 10,000 | 0.6340 | 2.2043 | 0.0097 |
| Julia | 10,000 | 0.6340 | 1.3700 | 0.0091 |
| Rust | 10,000 | 0.6337 | 1.5453 | 0.0082 |
| Fortran | 10,000 | 0.6338 | 1.2527 | 0.0090 |
Case2 : 非線形システム・ガウス
| language | #particles | RMSE | mean time [s] | std [s] |
|---|---|---|---|---|
| Python | 10,000 | 0.5030 | 2.1270 | 0.0200 |
| Julia | 10,000 | 0.5034 | 1.2020 | 0.0254 |
| Rust | 10,000 | 0.5033 | 1.4104 | 0.0166 |
| Fortran | 10,000 | 0.5029 | 1.1657 | 0.0222 |
Case3 : 非線形・非ガウス
| language | #particles | RMSE | mean time [s] | std [s] |
|---|---|---|---|---|
| Python | 10,000 | 0.8724 | 2.3667 | 0.0108 |
| Julia | 10,000 | 0.8698 | 1.5070 | 0.0071 |
| Rust | 10,000 | 0.8713 | 1.5207 | 0.0135 |
| Fortran | 10,000 | 0.8700 | 1.0984 | 0.0195 |
精度面では、言語による差はほぼ出ていませんが(同じアルゴリズムなので当然)、速度面では、今回のような小さな 1 次元モデルでも Python が飛びぬけて遅いことが確認できます。論文用の粒子フィルタのコードを Python で書いていた私にとっては結構なショックです。
Fortran が最速という、ある意味期待どおり(?)の結果になりましたが、それだけで「じゃあ全部 Fortran で書けばいい」と結論づけるのは早計です。ここではもう少し丁寧に結果を眺めてみます。
今回特に言及したいのは開発コストについてです。
ベースとなる実装は Python 版で、それをもとに Claude 4.5 Opus に「各言語版を書いてもらう」というフローで実装しています。
Rust / Fortran 版については、こちらで何度か修正・リファクタリング・最適化を加えたうえで今回の速度に到達しましたが、Julia 版だけは、一発出しのコードのままで、この速度を達成しているという経緯があります。
AI が一発出ししてくれたからという理由で「Julia は開発が簡単」とまでは言えませんが、書き下ろしの素朴なコードでも、コンパイラとランタイムがかなり良い線まで最適化してくれることが確認でき、Julia のスローガンである
Walks like Python, runs like C.
を達成していると感じます。
Julia が「書くだけでなぜか速い」のに対し、Rust は 「速くなるように書けば、ちゃんと速くなる」 という印象でした。
今回の結果では Fortran / Julia に次ぐ 3 番手となりましたが、Python よりは明確に高速です。ただし、この速度を出すためには、いくつかの明示的なチューニングが必要でした。
詳細は割愛・ソースコードを参照していただければと思いますが、複数の最適化を入れてようやく現在の速度に到達しています。
開発体験としては、コンパイラ(Borrow Checker)が非常に厳格なため、型やメモリの扱いについて曖昧なコードはそもそもコンパイルが通りません。この厳しさは「書きにくさ」にも繋がりますが、裏を返せば 「コンパイルさえ通れば、メモリ安全性が保証され、実行時に謎のセグフォで落ちることはかなり起きにくい」 という強力な安心感があります。数日かけた計算が、原因不明のメモリ破壊バグで落ちることはない気がするというのは、精神衛生上かなり良いポイントです。
実際にロボティクスの分野では Rust の利用も進んでいるようです(参考文献参照)。
Python はかなり遅いのですが、今回のテストは Python にとって不利であった感は否めません。Python の強みの一つである並列化や GPU 利用は、小規模モデルではオーバーヘッドのほうが勝ってしまい、強みを十分に活かせませんでした。開発コストについては作者の贔屓目によるバイアスが強く出るため、ここではあえて深入りしないことにします。
まとめ
今回は粒子フィルタにおける言語別の速度比較を行いました。
小規模データ・モデルという前提のもとでは、低レベルな数値計算が素で速い順番が、そのまま実行時間の順番として現れたのではないかと考えています。
一方で、
- 大規模モデルや GPU・並列化を前提とした場合
- あるいはロボティクスのように長期運用・安全性が重視される場合
には、また違った評価軸(開発コスト・エコシステム・メモリ安全性など)が効いてきます。
今回の結果はあくまで「小規模 1 次元 PF を CPU で回したときのスナップショット」として、言語選択の一つの参考にしていただければと思います。
参考文献
データ同化と計算量
https://www.riken.jp/press/2016/20160809_1/
https://essd.copernicus.org/preprints/essd-2025-26/essd-2025-26-ATC2.pdf
https://www.nature.com/articles/s41598-024-63053-4
Rao-Blackwellized Particle Filtering
https://arxiv.org/pdf/1301.3853
ロボティクスと Rust
https://maticrobots.com/blog/why-rust-its-the-safe-choice
https://medium.com/%40chetanmittaldev/rusts-safety-guarantees-and-real-time-capabilities-make-it-a-game-changer-in-the-field-of-robotics-3e042c474a3e
https://www.automate.org/tech-papers/building-functional-safety-at-speed-with-rust