データ同化入門:KF・EnKF・PFを使い分ける
総研大 統計科学コースの平元です。アドベントカレンダーを書くことになったのでデータ同化普及のための記事を書きます。
データ同化とは
データ同化(Data Assimilation)は、シミュレーションと現実の観測データを融合させ、より確からしい状態を推定する技術です。
元々は気象予報など地球科学の分野で発展した技術ですが、現在ではマーケティング分析や制御工学、デジタルツインなど、幅広い分野で応用されています。一言で言えば、「シミュレーションの計算結果」と「現実のデータ」をいいとこ取りして、真の状態を推定する手法です。
数理的な詳細は専門書(例:『データ同化入門: 次世代のシミュレーション技術』など)に譲りますが、本記事ではその基礎となる状態空間モデルと、代表的な3つの手法について解説します。
状態空間モデル
データ同化では、目に見えない「内部状態」から、目に見える「観測値」が生成されると考えます。
例えば、ある時系列データが以下のように得られたとしましょう。
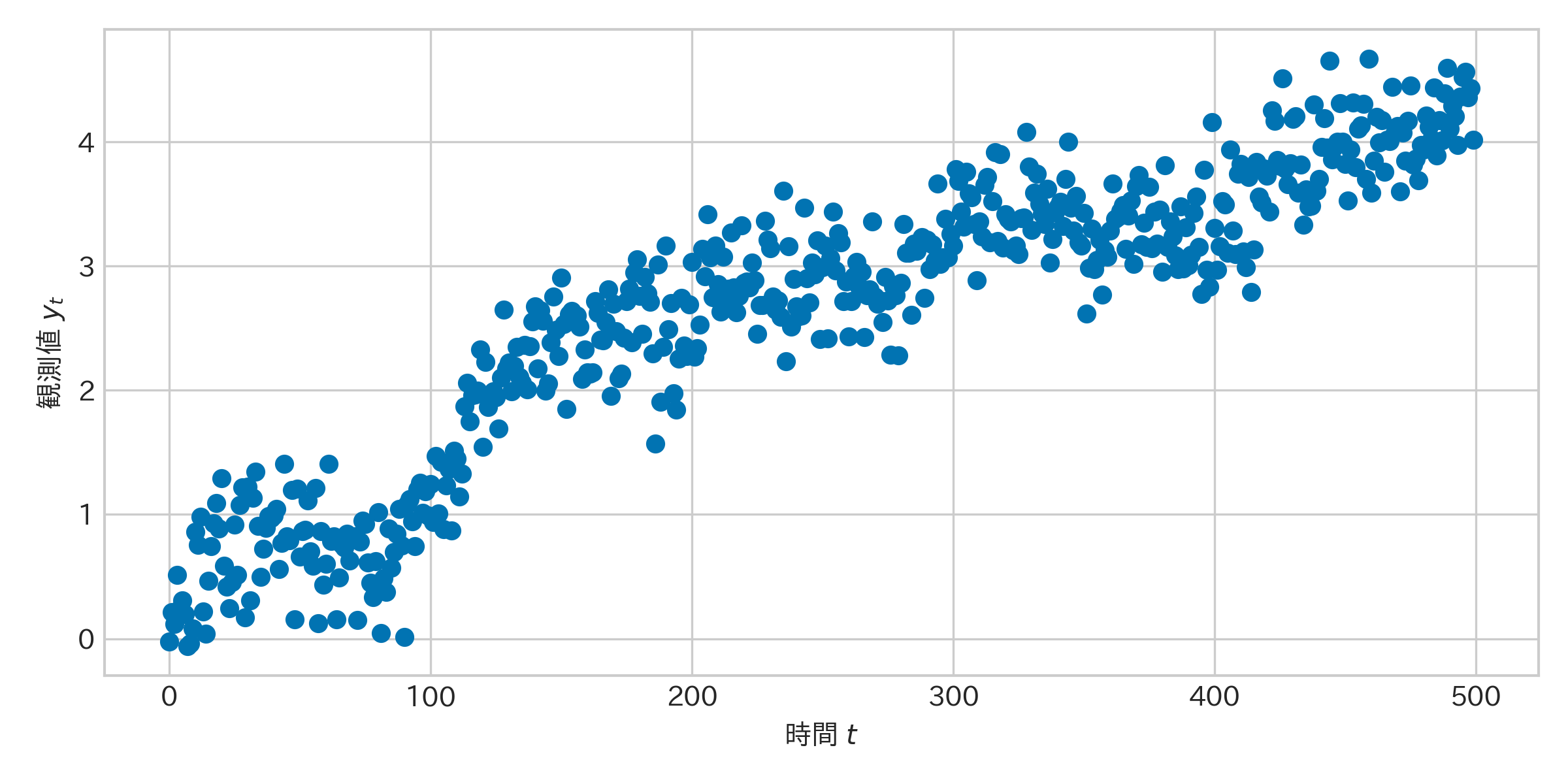
キャプション:観測されたデータ $Y_t$。ノイズを含んでおり、真の値は見えない。
このデータの「真の値」を推定するために、以下の状態空間モデルを定義します。
これを数式で表すと以下のようになります。
$$
\begin{aligned}
X_t &= F_t(X_{t-1}, v_t) \quad \text{(システムモデル)}
\end{aligned}
$$
$$
\begin{aligned}
Y_t &= H_t(X_t, w_t) \quad \text{(観測モデル)}
\end{aligned}
$$
ここで各変数は以下を表します。
- $X_t$: 状態変数(推定したい真の値。直接は見えない)
- $Y_t$: 観測変数(実際に得られるデータ)
- $F_t$: 状態が時間とともにどう変化するかを表す関数
- $H_t$: 内部状態がどのように観測値に変換されるかを表す関数
- $v_t, w_t$: それぞれシステムノイズ、観測ノイズ
このモデルにおいて、$F_t, H_t$ がある程度わかっているという仮定のもと、手元にある観測データ ${Y_1, Y_2, \dots, Y_t}$ を使って、見えない内部状態 $X_t$ を推定することがデータ同化の目的になります。
各手法の特徴と使い分け
前述の状態空間モデルにおいて、システムモデル $F_t$ や観測モデル $H_t$ が「線形か非線形か」、そしてノイズ $v_t, w_t$ が「正規分布(ガウス分布)に従うか否か」によって、適用できる手法が異なります。
代表的な3つの手法(KF, EnKF, PF)の違いを整理すると、以下のようになります。
| 比較項目 |
KF (カルマンフィルタ) |
EnKF (アンサンブルKF) |
PF (粒子フィルタ) |
|---|---|---|---|
| システムモデル | 線形のみ | 非線形 可 | 非線形 可 |
| 観測モデル | 線形のみ | 線形のみ | 非線形 可 |
| システムノイズ | ガウスのみ | ガウス (推奨) | 非ガウス 可 |
| 観測ノイズ | ガウスのみ | ガウス (推奨) | 非ガウス 可 |
| 計算コスト | 低 | 中 | 高 |
注記1:EnKFではガウス近似などの手法や観測モデルをシステムモデルに組み込むことで観測モデルを線形にするテクニックなどあり、観測モデルの適用可能性は意見が分かれるところですが、ここでは不可とします。
注記2:ENKF,PFにはそれぞれアンサンブル数という計算コストと精度のトレードオフになるパラメータがあり、計算コストは単純には言い切れないところがあります。
この違いは、主に「確率分布の形状をどう維持するか」というアプローチの差から生まれます。
1. KF (カルマンフィルタ):線形・ガウス分布
モデルが線形かつノイズがガウス分布であれば、状態変数の分布も常にガウス分布のまま保たれます。この場合、平均と分散だけを更新していけば良いため、カルマンゲインという計算式を用いて、計算コスト軽く、かつ数学的に厳密な最適解が得られます。
2. EnKF (アンサンブルカルマンフィルタ):非線形システムモデルへの拡張
モデルが非線形になると、分布の形状が歪み、単純な計算式では更新できなくなります。そこで、「多数のシミュレーション(アンサンブル)」を用意して分布を近似的に表現しつつ、更新ステップではKF同様にカルマンゲインの考え方を用いるのがEnKFです。計算コストと精度のバランスが良く、気象予報などの高次元モデルでよく使われます 。
3. PF (粒子フィルタ):あらゆる分布・モデルに対応
PFはカルマンゲインを使いません。代わりに、多数の粒子(真値の候補)をばら撒き、観測値との整合性(尤度)に応じて粒子の「生き残りやすさ(重み)」を調整します。
観測値と整合的な粒子を選び、矛盾する粒子を捨てることを繰り返し、粒子群の形状で分布形状を近似するため、分布が非ガウスの複雑な状況であったり、モデルが非線形でも柔軟に推定できるのが最大の特徴です。ただし、計算コストが重くなるという欠点もあります。
シミュレーションによる検証
実際にそれぞれの手法が適切そうな条件でシミュレーションをしてみます。グラフはシミュレーションに用いたデータの真値(青)と観測値(赤)です。
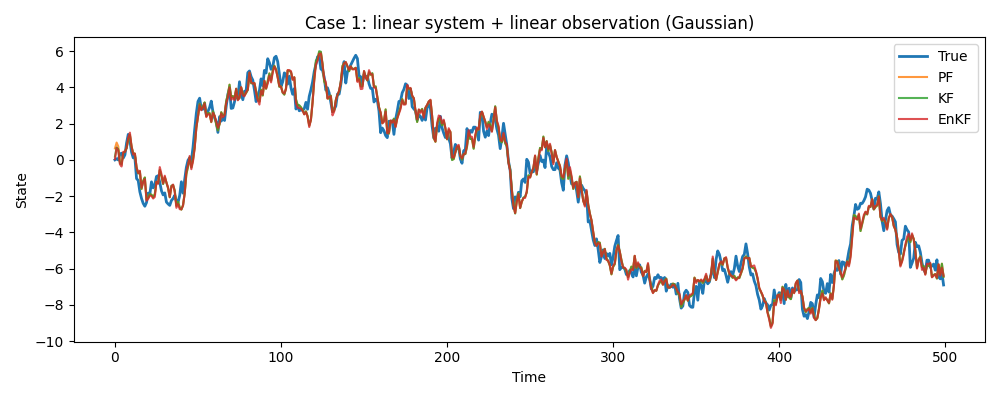
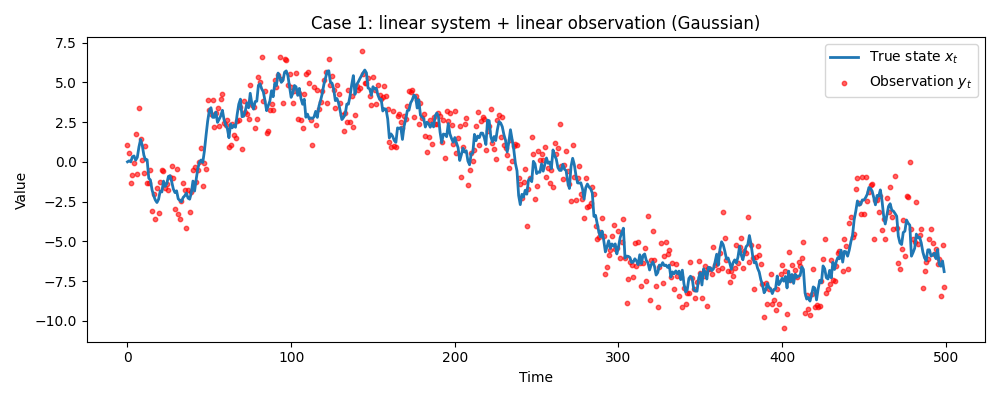
データ① 線形・ガウス
単純なランダムウォーク。状態の変化も、観測される値もすべて線形かつノイズが正規分布。カルマンフィルタが最も高速かつ高精度に推定できることが想定されます。
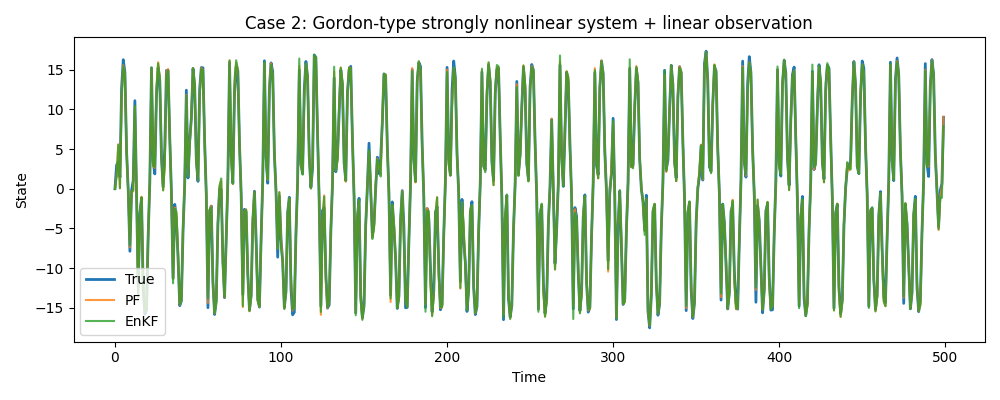
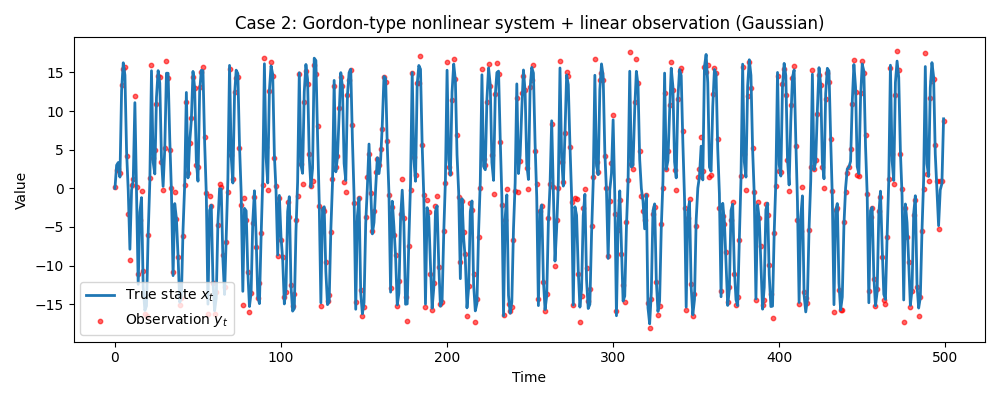
データ② 非線形システム・ガウス
システムモデルに非線形関数(Gordon et al. 1993のベンチマークモデル)を使用します。ただし、ノイズ自体は正規分布に従います。
$$x_t = 0.5 x_{t-1} + \frac{25 x_{t-1}}{1 + x_{t-1}^2} + 8 \cos(1.2t) + v_t$$
式が複雑なため、通常のKFでは扱えません(線形化誤差が大きすぎる)。EnKF(アンサンブルカルマンフィルタ)は粒子(アンサンブル)を使ってこの複雑な形状の変化をシミュレーションしますが、補正計算には「分布が正規分布に近い」という仮定を利用するため、PFよりも少ない計算量で現実的な解を出せます。
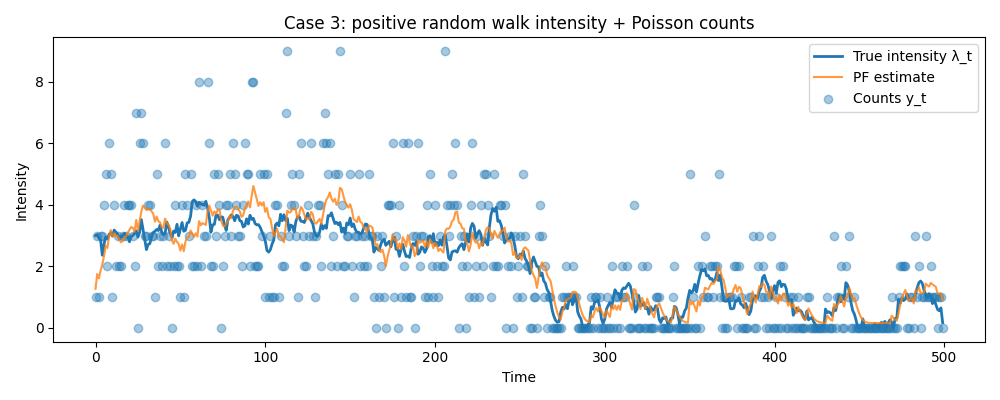
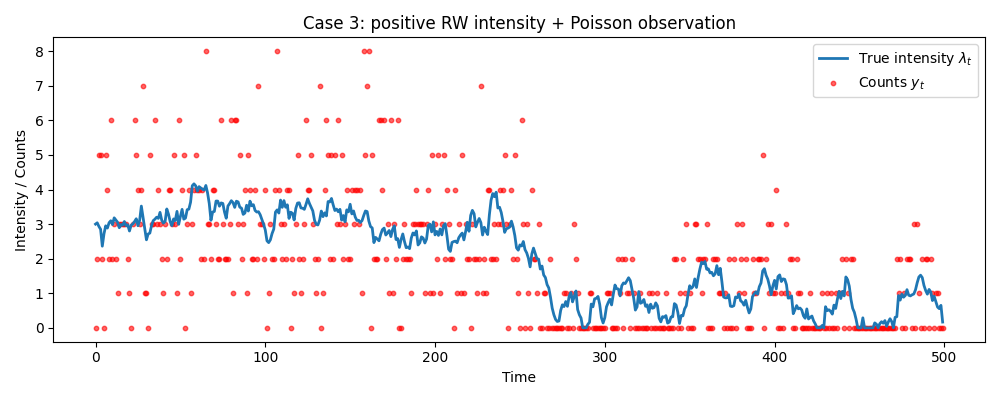
データ③ 非線形・非ガウス
最後は明確に非ガウスなケースです。
マーケティングデータや来客数のように、「0 以上の整数(カウントデータ)」のみが観測される状況を想定し、Poisson 観測モデルを用います。
$$
\begin{aligned}
\lambda_t &= \max(\lambda_{t-1} + v_t,\ \varepsilon),
\quad v_t \sim N(0, \sigma_v^2),\ \varepsilon > 0 \
\end{aligned}
$$
$$
y_t = \mathrm{Poisson}(\lambda_t)
$$
- $\lambda_t$:観測カウントの期待値(強度)
- $y_t$:実際に観測されるカウントデータ
$\lambda_t$ が負にならないように $\max(\cdot,\varepsilon)$ をとっているため、システムモデル自体も非線形になります。
観測は$\lambda_t$を期待値とした Poisson サンプリングであり、離散かつ非対称な非ガウス分布です。
このような設定では、KF / EnKF はガウス分布の仮定も、観測モデルが線形という仮定も適用できないため、使える手法はPFだけになります。
検証結果
それぞれのデータにおける推定精度(RMSE:二乗平均平方根誤差)と計算時間の比較、および時系列プロットは以下の通りです。
定量的な比較
| データ | 手法 | RMSE (精度) | 実行時間 (秒) |
|---|---|---|---|
| ① 線形・ガウス | KF (カルマン) | 0.634 | 0.002 |
| EnKF | 0.642 | 0.233 | |
| PF | 0.634 | 0.940 | |
| ② 非線形・ガウス | EnKF | 0.605 | 0.261 |
| PF (粒子) | 0.515 | 0.981 | |
| ③ 非線形・非ガウス | PF (粒子) | 0.892 | 0.998 |
※ RMSEは値が小さいほど真値に近いことを表します。
※ PFの粒子数は10,000、EnKFのアンサンブルサイズは100で実施しています。
データ① 線形・ガウスの場合
KF, EnKF, PF いずれもほぼ同等のRMSE(約0.63)を出しており、真値(青線)を正しく追従できています。
一方で速度について、 KFは 0.002秒 と一瞬ですが、PFは約1秒かかっています。EnKFはその中間ですね。
データ② 強非線形システムの場合
システムモデルが非常に複雑(Gordonモデル)なため、単純な線形近似では追従困難なケースですが、EnKF(緑線)はPF(オレンジ線)とほぼ同様に真値を捉えています。RMSEを見るとPF(0.515)の方が若干優秀ですが、(特にPFは)乱数の機嫌やアンサンブル数の選択もあるのでEnKF(0.605)と同等という解釈で良いと思います。EnKFはPFの約4倍高速であり、分布を仮定することで計算が軽いEnKFの特性が良く出ているのではないかと思います。
データ③ 非ガウス(ポアソン観測)の場合
グラフの青い点は実際の観測値を表します。
ポアソン分布・離散分布はそもそもKF/EnKFでは扱うことができない分布(工夫次第ではできなくもない)ですが、PFだと時間変化するポアソン分布期待値を正しく追えていることが確認できます。
まとめ
1.線形・ガウス分布 $\rightarrow$ KF (最速・最適)
2.システムモデルが非線形・ガウス分布 $\rightarrow$ EnKF (計算コストと精度のバランス良し)
3.観測モデルが非線形 $\rightarrow$ PF (計算コストは高いが、どんな分布でも扱える)
実務でデータ同化を行う際は、まず観測モデルが非線形か,システムノイズ・観測ノイズはガウス分布か,システムモデルは線形化を見つつ、計算リソースと相談しながら適切な手法を選択してみてください。
$$