More than 3 years have passed since last update.

株式会社LIFULL

【R】可視化で理解するベイズ推定

Last updated at 2020-04-29Posted at 2020-04-29

#はじめに

###◎モチベーション

　RのbayesABやPythonのPyMC3といったベイズ統計ライブラリの登場により, マシンを使ったベイズ推定の実行負荷は年々軽くなってきている.

　実際, プロセスをゼロから理解しなくてもweb上に散見される事前分布と確率密度関数の組み合わせをを参考にすれば, なんとなく実行まではこじつけられる. しかし, 中身をしっかり理解したい, または実務で応用したい者もいるだろう.

　今回は, 二項分布を例にベイズ推定(事後分布の推定)の計算に必要となる構成要素に分解し, 計算プロセスを可視化しながら丁寧に確認する. その上でまずは, ベイズ推定を簡単に定義する.

###◎対象読者

　ベイズ統計に興味がある...

データアナリスト
データサイエンティスト

###◎統計理論

ベイズ推定
二項分布
ベータ分布

###◎使用言語

###◎構成

確率密度関数
尤度関数と最尤推定量
事前分布
事後分布とMAP推定量
マルコフ連鎖モンテカルロ法

#ベイズ推定: 二項分布のパラメータθの事後分布を求める

###◎ベイズ推定とは?

　一般に, ベイズ推定とはベイズの定理を使った確率的推論の方法論である. ベイズの定理とは, 異なる2つの事象をAとBで定義した時, P(A)>0で以下の式が成り立つ.
　　

\begin{eqnarray*}
 P(B|A) = \frac{P(A|B)P(B)}{P(A)}\\
\end{eqnarray*}

P(B|A) \varpropto P(A|B)P(B) = P(A, B)\\

　　
　上記の通り, 条件付き確率*P(A|B)と事前確率P(B)*の積は, *P(A|B)の逆確率であるP(B|A)に比例することが分かっている. また, 上式の分母P(A)*は正規化定数として省略され, 下式のようにカーネルのみが考慮されることが多い.

　このベイズの定理を統計学に当てはめて考えるのがベイズ統計であり, 具体的には事象Aに観測されたデータX, 事象Bにモデルのパラメータ(μやθなど..)を想定することが多い.

　またベイズ統計では, 前提としてモデルのパラメータが確率変数と定義(頻度主義では定数)する. 最終的には, 観測データ(事象A)を条件とするパラメータ(事象B)の発生確率を事後分布*P(B|A)*として獲得することを目的とする.

　ちなみに事前確率*P(B)は, しばしば計算主によって経験的に決められることがあるため主観確率(subjective probability)*などと呼ばれ, これが一部の人間からベイズ推論の欠点として指摘される根拠の1つとなる.

　以降では, 実際に有名なコイン投げを例に二項分布におけるパラメータθの事後分布*P(B|A)*の推定を行う.

###◎問題設定

　今回は, 表と裏を持つコイン投げをテーマに表が出る確率をベイズ推定する.
　まず, このコインの名前を「コインA」とする. いま試しにコインAを100回投げてみると, 表が56回出た.
　この時, このコインの表が出る確率θをベイズ推定を使って求めたい.

##1. 確率密度関数

　確率密度関数*(PDF: probability density function)とは, 連続型確率変数Xがある値xを取りうる確率Pを求めるための関数ｆ*のことである.

　PDF: P(a \leq X \leq b) = \int_{a}^{b}f(x)dx

　PDFは, 区間積分をすることで確率変数がある範囲の値をとる確率を求めることもできる. なお, 確率密度関数の値域は非負の実数であり, 定義域全体を積分すると1となる.

　ちなみに, 確率変数Xがコインの裏表*(0 or 1)のように離散値である離散型確率変数であるときは, 確率質量関数(PMF: probability mass function)*として区別されることもある.

###◎二項分布*(Binomial Dsitribution)*

　まずこのコインAの表が出た回数xは二項分布*(Binomial Dsitribution)に従う. 二項分布とは, 「ベルヌーイ試行(結果が成功か失敗のいずれかとなる試行)を独立にn回行った」ときの成功回数X*が従う分布である.

　二項分布の未知パラメータは, 成功確率θの1つである(試行回数nは必然的に決まる). また, 確率質量関数は以下で定義される.

PMF_{Binom}: p(x|\theta)=\Biggr(
\begin{matrix}
n\\
x
\end{matrix}
\Biggl)
\theta^x(1-\theta)^{n-x}

　　
　最後に今回コインAは, 「100回投げてみると, 表が56回出た」のでまずはそのデータを用意する.

# 今回はsum(data)=56となった
data<-rbinom(100, 1, 0.56)
data[1:3]

>>> output: 1
>>> output: 1
>>> output: 0

##2. 尤度関数と最尤推定量

　最尤推定法*(MLE: maximum likelihood estimation)は, データXが従う母集団分布が既知であるがパラメータθの値が未知のとき, 観測データx*を用いてパラメータを点推定する方法である.

　具体的にMLEでは, 尤度関数*(likelihood function)*を最大化する推定値$\hat{\theta}$を最尤推定量とする.

###◎尤度関数*(likelihood function)*

　そして尤度関数は以下の通り, 確率密度関数*(PDF)*の積で与えられている.
　　

\begin{eqnarray*}
 L_{Binom}: l(x|\theta)= \prod_{i=1}^n 
\Biggr(
\begin{matrix}
n\\
x
\end{matrix}
\Biggl)
\theta^x(1-\theta)^{n-x}\\
\end{eqnarray*}

　　
　上記から分かるように, 確率密度関数*(PDF)と尤度関数(LF)*の式自体に差異はない. ただ, 「尤度」と「確率密度」では意味合いが異なる.

　尤度を理解するキーワードは, 尤度は「"ある仮説"の尤もらしさ」を意味するということである. ではこの"ある仮説"が何かというと「手元のデータxが観察された状況において, 母集団分布のパラメータがθである」という仮説の尤もらしさであり, 任意のθの値によって尤もらしさも異なるという構造になっている.

　これを英語では, likelihood for a hypothesis given a set of observationsなどと表現される. 仮説という時点ですでに頻度主義の統計学の匂いがするが, 最尤推定法は頻度論の考え方に基づいた推定らしい.

　以上より今回の例に当てはめると, いま手元にある観測データ(x=56, n=100)という結果を受け, 尤度の考え方に基づいて「尤もらしい」パラメータの値を推定する. 　　

　それでは二項分布の尤度関数を求めるための自作関数を作り, 手元のデータに基づく尤度(関数)を可視化する.

# 尤度関数
likelihood_binom<-function(p){
    p^sum(data)*(1-p)^(length(data)-sum(data))
}

options(repr.plot.width=14, repr.plot.height=8)
plot(seq(0,1,0.01), likelihood_binom(seq(0,1,0.01)), type="h", col="#fff7ef", lwd=13, bty="n")
par(new=T)
plot(seq(0,1,0.01), likelihood_binom(seq(0,1,0.01)), type="l", col="#ffdbdb", lwd=6, bty="n")
grid()

　どうやら, θ=0.56あたりで尤度が最大となっている風である.

###◎対数尤度関数(log-likelihood function)

　最尤推定法では, 尤度関数における尤度(確率)が最大値をとるパラメータの値を解析的に求めるために偏微分方程式を解く必要がある.

　今回のような二項分布とベータ分布の同時確率におけるパラメータの最尤推定ならまだ簡単なものの, 尤度と事前分布の組み合わせ次第では面倒な計算となる. そこで以下のように, 計算を楽にするために積関数(尤度関数)の対数をとる.
　　

\begin{eqnarray*}
 \log L_{Binom}: \log l(x|\theta) &=& \sum_{i=1}^n \log \Bigr(
\Biggr(
\begin{matrix}
n\\
x
\end{matrix}
\Biggl)
\theta^x(1-\theta)^{n-x}\Bigl)\\
&=& \sum_{i=1}^n \log \Biggr(
\begin{matrix}
n\\
x
\end{matrix}
\Biggl)+x\log(\theta)+(n-x)\log(1-\theta)\\
\end{eqnarray*}

　それでは, 先ほど求めた尤度関数の対数を取った対数尤度関数を確認する.

#log_likelihood_binom<-function(p){
#    log(p^sum(data)*(1-p)^(length(data)-sum(data)))
#}
# 対数尤度
log_likelihood_binom<-function(p){
    sum(data)*log(p)+(length(data)-sum(data))*log(1-p)
}

plot(seq(0,1,0.01), log_likelihood_binom(seq(0,1,0.01)), type="h", col="#fff7ef", lwd=13, bty="n")
par(new=T)
plot(seq(0,1,0.01), log_likelihood_binom(seq(0,1,0.01)), type="l", col="#ffdbdb", lwd=6, bty="n")
grid()

　普通の尤度関数と同じく, 目視ではθ=0.56あたりで対数尤度が最大となっているように見える.

###◎最尤推定量(MLE: maximum likelihood estimation)

　最後に最尤推定量を実際に求める. すでに紹介した通り, 最尤推定では以下のように尤度関数L(θ)を最大化するθを求める.
　　

 MLE_\hat{\theta}: argmax_{\theta} \log l(x|\theta)\\

　　
　先ほど求めた, 対数尤度関数l(θ)をθについて偏微分する.
　　

\begin{eqnarray*}
 \log l'(x|\theta)
 &=& \frac{\partial l(\theta)}{\partial \theta}\\
 &=& \frac{\partial}{\partial \theta}x\log(\theta)+\frac{\partial}{\partial \theta}(n-x)\log(1-\theta)\\
 &=& \frac{x}{\theta}-\frac{n-x}{1-\theta}\\
\end{eqnarray*}

　　
　対数尤度関数は上に凸のグラフだったため, 変化量つまり傾きが0のとき最大値を取る.
　　

\frac{x}{\theta}-\frac{n-x}{1-\theta} = 0\\
\theta=\frac{x}{n}\\

　　
　それではRでも, 尤度関数における尤度(確率)が最大値をとるパラメータの値を求めるために, *logL(θ)*偏微分方程式を計算する.

# 対数尤度の最尤推定値
log_mle<-optimize(function(p) log_likelihood_binom(p), interval=c(0, 1), maximum=T)$maximum
log_mle
# 尤度の最尤推定値
mle<-optimize(function(p) likelihood_binom(p), interval=c(0, 1), maximum=T)$maximum
mle

>>> output: 0.560000538337665
>>> output: 0.559999072963702

　上記から対数尤度関数から求めた最尤推定量*(MLE)は, およそθ=0.56*となった.

##3. 事前分布(Prior Distribution)

　ベイズ推定では, 事前確率を導入することで事後確率を求めることができた. ここでは, その事前確率の設定プロセスを確認する.

　まず重要な点として, 推定対象となるパラメータが従う分布を把握している場合はそれらを事前分布とすればいいが, 一方で誤った事前分布を用いることで推定の結果や信頼性を損なう危険性がある.

　そこで, 事前確率が未知の場合は一様分布や以降で説明する共役事前分布などの無情報事前分布*(non-informative prior distribution)*を用いる.

###◎共役事前分布*(Conjugate Prior Distribution)*

　事前分布のうち, 事後分布が事前分布として選択した確率分布と一致するものを共役事前分布*(conjugate prior distribution)*と呼ぶ.　

　今回の(尤度関数が)二項分布の例で言えば, 事前分布としてベータ分布を用いると事後分布もベータ分布となる. なお, 主要な尤度関数と共役事前分布の組み合わせはこちらから確認できる.

###◎ベータ分布*(Beta Distribution)*

　今回は前述した通り, 事前分布としてベータ分布を用いる. ベータ分布の確率密度関数は以下で定義される.
　　

\begin{eqnarray*}
Beta(\theta|\alpha, \beta)= \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}\\
\end{eqnarray*}
\quad \alpha, \beta >1 \quad 0 \leq \theta \leq 1

　　
　上記の通りベータ分布は, αとβの2つをパラメータに持つ. また, 期待値と分散は以下で定義される.
　　

　E(X)=\frac{\alpha}{\alpha+\beta}\\
　V(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}

　　
　今回は事前知識(主観確率)として, コインの裏表が出る確率はそれぞれE(X)=50%で同等であり, 誤差を考慮しても標準偏差*SD=5%*ほどであるという情報があると仮定する.

　この事前知識を期待値と分散の公式の左辺に当てはめ, αとβの連立方程式の解くことでベータ分布のパラメータが求められる自作関数を以下で定義したので実際に計算してみる.

# http://www.okadajp.org/RWiki/?%E9%80%A3%E7%AB%8B%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%82%92%E8%A7%A3%E3%81%8F
library(nleqslv)

find_beta_params<-function(x, e_x, v_x){
    alpha=x[1]
    beta=x[2]
    c(e_x-alpha/(alpha+beta), v_x-(alpha*beta)/(((alpha+beta)**2)*(alpha+beta+1)))
}

fn<-function(x){
    find_beta_params(x, 0.5, (0.05)**2)
}

ans<-nleqslv(c(1,1), fn)
ans$x

>>> output: 49.4999986768254
>>> output: 49.4999981716322

　上記より, 期待値E(X)=0.5かつ標準偏差SD=0.05となるベータ分布のパラメータはおよそα, β≒50ということがわかった.

###◎ベータ分布の確率密度関数

　ベイズの定理より, 事後確率の実際の計算では尤度関数に事前確率分布を掛ける必要がある. ベータ分布の確率密度関数は以下で定義される.
　　

\begin{eqnarray*}
PDF_{Beta}: p(\theta|\alpha, \beta)= \prod_{i=1}^n \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}\\
\end{eqnarray*}

　　
　また, 上記の対数を取ると以下になる. ※事前分布と尤度の積を求めるときに使う
　　

\begin{eqnarray*}
 \log PDF_{Beta}: p(\theta|\alpha, \beta)
 &=& \sum_{i=1}^n \log\Bigl(\frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)}\Bigr)\\
 &=& \sum_{i=1}^n \Bigl((\alpha-1)\log\theta+(\beta-1)\log(1-\theta)-\log(B(\alpha, \beta))\Bigr)\\
\end{eqnarray*}

　　
　ここで, パラメータα, β=50のベータ分布の確率密度関数と対数化した場合をそれぞれ可視化してみる.

# α, β=50のベータ分布の確率密度関数
beta_dist<-function(p, alpha, beta){
    (p^(alpha-1)*(1-p)^(beta-1))/((gamma(alpha)*gamma(beta))/gamma(alpha+beta))
}

prior_beta<-function(p){
    beta_dist(p, 50, 50)
}

plot(seq(0,1,0.01), prior_beta(seq(0,1,0.01)), type="h", col="#effff7", lwd=13, bty="n")
par(new=T)
plot(seq(0,1,0.01), prior_beta(seq(0,1,0.01)), type="l", col="#8ec6ff", lwd=6, bty="n")
grid()

# α, β=50のベータ分布の確率密度関数の対数化
log_prior_beta<-function(p){
    log(beta_dist(p, 50, 50))
}
plot(seq(0,1,0.01), log_prior_beta(seq(0,1,0.01)), type="h", col="#effff7", lwd=13, bty="n")
par(new=T)
plot(seq(0,1,0.01), log_prior_beta(seq(0,1,0.01)), type="l", col="#8ec6ff", lwd=6, bty="n")
grid()

　ようやく, 尤度(二項分布)と共役事前分布(ベータ分布)の役者が出揃ったので, 以降では事後分布の推定に移る.

##4. 事後分布(Posterior Distribution)
　　
　ベイズの定理より, 事後確率は事前確率に尤度関数の積で求めることができる. 今回の例では, データxが与えられた二項分布を尤度関数に, パラメータα, β=50が与えられたベータ分布を事前分布とする. 事後分布は, この2つの確率の相乗となるため以下で定義される.
　　

\begin{eqnarray*}
 f(\theta|x)
 &=& \prod_{i=1}^n L_{Binom} PDF_{Beta}\\
 &=& \sum_{i=1}^n \log L_{Binom} + \log PDF_{Beta}\\
\end{eqnarray*}

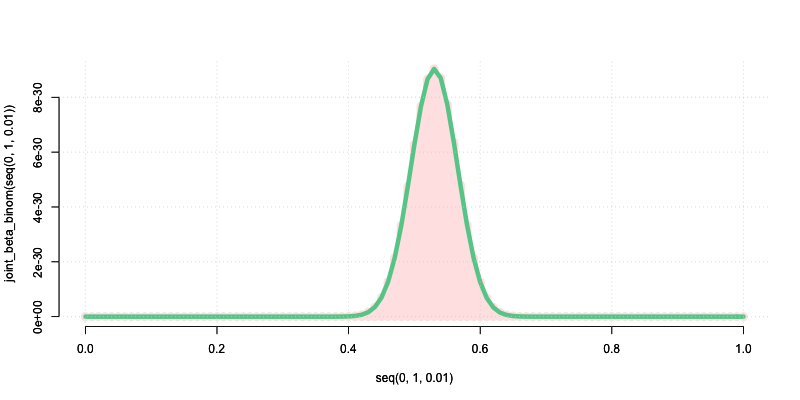
　それでは実際に, 事後分布を計算して可視化してみる.

#尤度×事前分布
joint_beta_binom<-function(p){
    likelihood_binom(p)*prior_beta(p)
}

plot(seq(0,1,0.01), joint_beta_binom(seq(0,1,0.01)), type="h", col="#fff4ea", lwd=12, bty="n")
par(new=T)
plot(seq(0,1,0.01), joint_beta_binom(seq(0,1,0.01)), type="l", col="#ff7f00", lwd=6, bty="n")
grid()

　最後に, 上記で求めた事後分布をもとに点推定によって最終的なパラメータθの推定量を決める.

###◎MAP推定*(maximum a posteriori)*

　MAP推定量は, 事後分布における最頻値を最大事後確率点として点推定する手法である. 誤解されやすい点として, ベイズ推定は「事後分布」全体(あるいはそのもの)をoutputとするため, パラメータθを特定の値に定めたい(点推定)場合はもう一工夫必要という訳である.
　　

 MAP_\hat{\theta} : argmax_\theta \hspace{3pt} \sum_{i=1}^n \Bigl(\log L_{Binomial}+\log L_{Beta}\Bigr)\\

　それでは, MAP推定量$\hat{\theta}$を実際に求める.

map<-optimize(function(p) joint_beta_binom(p), interval=c(0, 1), maximum=T)$maximum
map

>>> output: 0.530319646507133

　MAP推定量$\hat{\theta}$は, およそ0.53となった. 以上, 最尤推定量からMAP推定量に至るまでの変化をまとめると以下となる.

手元にある二項分布に従うコインAの結果xの最大尤度が約56%.
ベータ分布に従う事前分布の最頻値が約50%.
事後分布の最頻値を意味するMAP推定量が約53%.

　上記から, 最尤推定量は事前確率によって修正され, コインの表率としてよりふさわしい値だと考えられるMAP推定量となった. このようにベイズ推定は, サンプルサイズが小さいときに推定量が不安定となる最尤法の欠点を克服できるメリットがある.

##5. マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods)

###◎ベイズ推定におけるMCMC導入の背景

　上記の例では, 関数f(θ)を解析的に特定してから事後確率をもとにMAP推定量などの点推定値を求めた. しかし, パラメータが複数あるとき多重積分となり, 計算コストが跳ね上がったり最悪関数を特定できない(数式で表せない)ケースがある.

　これを乱数シミュレーションにより事後分布を再現することで, 中央値*(MED)や期待値(EAP), 最頻値(MAP)など度数を基にして点推定値を手に入れようという代案がベイズ推定におけるMCMC*の導入の背景となる. 手に入れたサンプルをもとにモンテカルロ積分を使うことで, MCMCサンプルの和で表現できる.

###◎マルコフ連鎖*(Markov chain)*

　まずマルコフ連鎖そのものは, 現在のサンプルの値*(t)が1時点前のサンプルの値(t-1)*にのみ依存して発生するというルール(マルコフ性)に従う確率過程から生まれたサンプル列を意味する言葉である. また, モンテカルロ法とは乱数を用いてシミュレーションや数値計算を行う手法の総称であった.

　ただ, ベイズ推定の文脈でマルコフ連鎖を理解するキーワードは「提案分布*(proposal distribution)」と「遷移確率(transition probability)」である. MCMCでは, 現在(t)のサンプルを軸とする提案分布によって定義された遷移確率に従い, 次の時点(t+1)*となる遷移先候補のサンプルが抽出される.

　数学的には, t時点の状態ベクトルを遷移確率行列*(transition probability matrix)による線形写像を用いることでt+1時点の状態ベクトルを手に入れている. 遷移確率行列はマルコフ過程の全時点において一定であるため, その結果マルコフ連鎖は定常分布(stationary distribution)*となる.

###◎モンテカルロ法*(Monte Carlo methods)*

　モンテカルロ・シミュレーションでは, サンプリング方法に色を付けるアルゴリズムが重要となる. MCMCにおけるアルゴリズムを理解するためのキーワードは, 「目標分布*(target distribution)」と「詳細つりあい条件(detailed balance)*」である.

　前提として, 乱数のサンプリングのゴールはベイズの定理で手に入れた事後分布(今回はベータ分布)を再現することであった. これをベイズ推定におけるMCMCでは, 目標分布*(target distribution)*と表現する.

　そして, 前述した"提案"される候補サンプルは以降で詳細を説明するメトロポリス法などのアルゴリズムに渡される. そして, 最終的にマルコフ連鎖に加える正式なサンプルとして受容するか棄却するか, 棄却した場合代わりに何をサンプルとして採択するかが決められる. この目標分布*(target distribution)*を目指す上で必要となる, 候補サンプルの採択ロジックを詳細つりあい条件と呼ぶ.

　詳細つりあい条件を満たしたMCMCサンプリングの結果は, マルコフ連鎖がt→∞になるに従って目標分布(ここではベイズの定理で手に入れた事後分布)に収束することが期待される.

###◎メトロポリス・アルゴリズム*(Metropolis algorithm)*

　今回は, メトロポリス・ヘイスティングス法*(Metropolis-Hastings algorithm)*の一種であるメトロポリス法を用いて, 先ほどの事前確率と尤度から成る事後分布を乱数シミュレーションで再現する.

　メトロポリス・アルゴリズムの手順は, 以下となる.

初期化: 初期値*(t=0)*と遷移確率も持つ提案分布として任意の確率密度関数(今回は一様分布)を決める
候補サンプルの生成: 次時点*(t=t+1)*の候補サンプルを現時点を軸とする提案分布から生成する
採択率の定義: 採択率*α**(acceptance ratio)を事後オッズ比(posterior odds ratio)*から求める
採択/棄却の判定: 採択率αがα≧1または, αが提案分布から生成した別のサンプル以上のいずれかを満たすとき, 候補サンプルを次時点の正式サンプルとして採択. 満たさない場合は, 候補サンプルを棄却し, 再び現時点の値を採択する.
これを最終的に必要なマルコフ連鎖の長さの分だけをt回繰り返す

# メトロポリス・アルゴリズム
mcmc_metropolis<-function(current_parameter){
    proposed_parameter=runif(n=1, min=0, max=1)
    post_odds=joint_beta_binom(proposed_parameter)/joint_beta_binom(current_parameter)
# metropolis method: acceptance_ratioが1以上, または一様分布からの適当な0<rs<1の乱数rs以上の時に提案値を受容
    acceptance_ratio=min(1, post_odds)
    if(acceptance_ratio>=runif(n=1, min=0, max=1)){
        proposed_parameter
    }else{
        current_parameter
    }
}

　メトロポリス・アルゴリズムのロジックを書くことができたので, 実際に初期状態*(t=0)を含めて5001期分(nsteps)のサンプルを乱数シミュレーションして手に入れる. また今回は, このシミュレーション自体を3回(niter)*繰り替えすプログラムを走らせる.

　また, MCMCでは初期のサンプルは任意に決めた初期値に依存してしまうので, burn-in期間として切り捨てることが多い. よって, 最期*(5001)から全体の後半約2/5*となるサンプルだけを対象にシミュレーション結果を可視化する.

niter<-3
nsteps<-5000
mcmc_samples<-c()

for (i in 1:niter) {
    
    mcmc_sample<-rep(NA, 5001)
    mcmc_sample[1]<-0.5 #初期値
    
    for (t in 1:nsteps) {
        mcmc_sample[t+1]<-mcmc_metropolis(selected_parameter=mcmc_sample[t])
    }
    mcmc_samples[i]<-mcmc_sample
}

plot(mcmc_sample[-(1:2000)], type="l", col="#89ff89", lwd=6, bty="n")
par(new=T)
plot(mcmc_sample2[-(1:2000)], type="l", col="#89c4ff", lwd=6, ylab="", yaxt="n", bty="n")
par(new=T)
plot(mcmc_sample3[-(1:2000)], type="l", col="#ffc489", lwd=6, ylab="", yaxt="n", bty="n")

　最後に, 上記のサンプリング結果をモンテカルロ積分のイメージに倣ってわかりやすくヒストグラムで表現する.

hist(mcmc_sample[-(1:2000)], col="#89ff89", breaks=seq(.4,.7,0.005), lwd=6, bty="n")
hist(mcmc_sample2[-(1:2000)], col="#89c4ff", breaks=seq(.4,.7,0.005), lwd=6, xlab="",ylab="", yaxt="n", bty="n", add=T)
hist(mcmc_sample3[-(1:2000)], col="#ffc489", breaks=seq(.4,.7,0.005), lwd=6, xlab="", ylab="", yaxt="n", bty="n", add=T)

　MCMCを使わずに求めたMAP推定量は, おおよそθ=0.53だった. そしてMCMCの結果は, 上のヒストグラムより最頻値が同じく0.53周辺となっていることが確認できる. 以上が, メトロポリス法を使ったMCMCサンプリングとなる.

#さいごに

　今回は, ベイズ推定の過程を一つずつ可視化した. また, パラメータが単一の事後分布を例としたためMCMCを使うまでもなかったが, あえてメトロポリス法によるサンプリングを最後に付け加えた. 本記事が, 読者にとって視覚情報によるさらなる理解のきっかけとなれば幸いである.

　次回は, ベイズ統計を使った仮説検定をまとめる.

##◎参考文献

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up