はじめに
多くの人にとって、初めてモンテカルロ法に触れるのは「ダーツを投げて円周率を求めるプログラム」だと思う。プログラムは簡単だけれど、そこそこの桁数を得るのに相当な試行回数が必要になるので、他のもっと収束が早い公式と比較したりして「モンテカルロ法は遅い」という印象を持ってしまう。
しかし、現在一般に「モンテカルロ法」というと、ほぼ「マルコフ連鎖モンテカルロ法(Markov-Chain Monte Carlo, MCMC)を指す。マルコフ連鎖モンテカルロ法は他の高次元数値積分法に比べて収束が早く、かつ他の近似手法と違って得られる答えにバイアスが無いという特徴があり、極めて強力な手法である。
さて、マルコフ連鎖モンテカルロ法を習得するにあたって、初学者1の鬼門は詳細釣り合い条件(Detailed Balance)だと思う。詳細釣り合い条件の次に、メトロポリス法や熱浴法などで遷移確率を決めるが、教科書を読んでもその違いがよくわからない、ということもありがちであろう。そこで、数式で証明されても、実際に簡単な系で確認したりスクリプト書いてみないと理解した気になれない人(=僕)のために、モンテカルロ法における詳細釣り合い条件と遷移確率の決め方についてざっくりと説明してみる。なお、数式を使った証明はしない(教科書に書いてあるから)。
詳細釣り合い条件
いくつかの状態がある系を考える。状態$i$にはエネルギー$E_i$が定義されている。この時、温度を$T$として、最終的に状態$i$をボルツマン重み$\exp(-E_i/kT)$の確率でサンプリングしたい。状態が与えられればエネルギーはすぐ計算できるが、あるエネルギーを持っている状態が何個あるかは事前にはわからないのがミソである2。そこで、状態$i$から状態$j$への遷移確率$P(i\rightarrow j)$を適当に決めることで、平衡状態が各状態のボルツマン重みに比例するようにしたい。そのために使われるのが詳細釣り合い条件である。
状態Aと状態Bの間の遷移を考える。それぞれエネルギーは$E_A$と$E_B$とする。平衡状態における存在確率$\pi_A, \pi_B$は、
\begin{align}
\pi_A &= \frac{\exp(-\beta E_A) }{\exp(-\beta E_A) + \exp(-\beta E_B)}\\
\pi_B &= \frac{\exp(-\beta E_B)}{\exp(-\beta E_A) + \exp(-\beta E_B)}
\end{align}
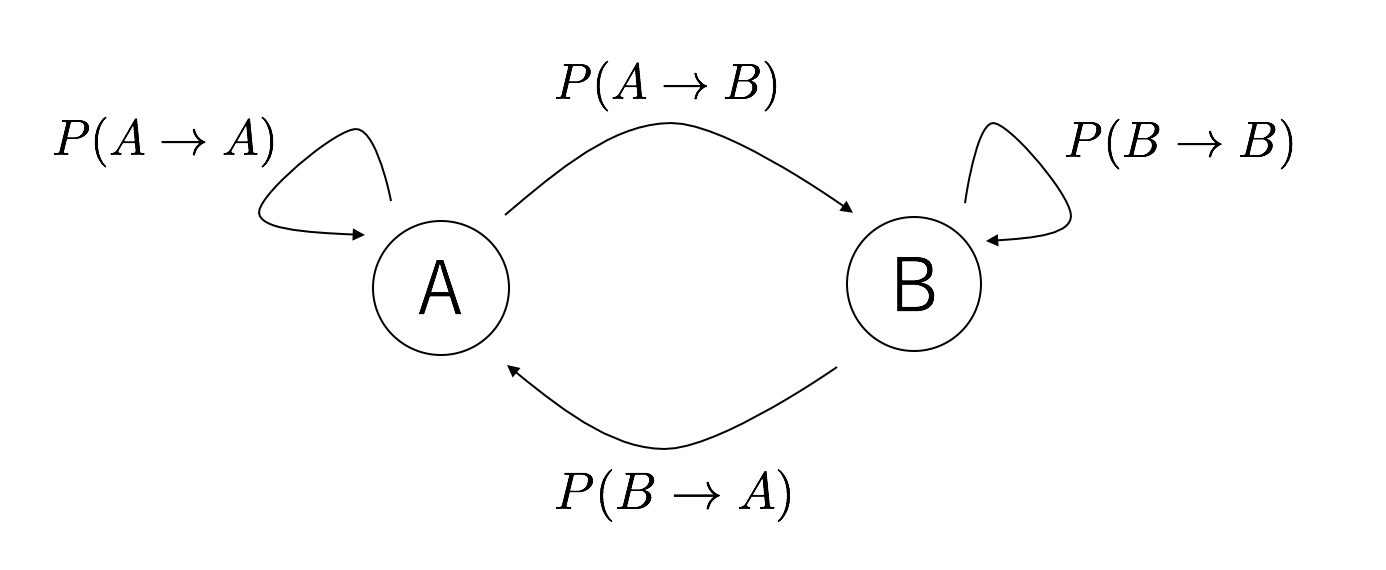
となる。ただし$\beta$は逆温度で$\beta=1/kT$である。状態遷移図はこんな感じになる3。
さて、系が平衡状態にあるとしよう。平衡状態にある場合は、遷移確率に従って状態が遷移してもそれぞれの存在確率が変わってはいけない。
従って、いまAにいる奴らがBに行く割合と、いまBにいく奴らがAに行く割合が等しくなければならない。式で書くとこんな感じ。
$$
\pi_A P(A \rightarrow B) = \pi_B P(B \rightarrow A)
$$
$\pi_A$、$\pi_B$はそれぞれの国にいる人の人口で、$P(A \rightarrow B)$は、A国にいる人のうちどのくらいの割合がB国に移住するかを表している。上記の条件が満たされていれば、移住(遷移)の後でも人口が変わらないのがわかると思う。この条件を詳細釣り合い条件と呼ぶ。「詳細(detailed)」とついているのは、全ての状態間についてこの条件が成立することを要求しているためで、実はこの条件は緩めることができるのだが、ここでは扱わない。
熱浴法とメトロポリス法
さて、先程の2状態の遷移図において、決めなければならない確率は4つある。AやBから出ていく確率(自分に戻る矢印も含める)の総和がそれぞれ1であるという確率の保存則から条件が2つ出てくる。それに詳細釣り合い条件を含めても条件が3つしかない。決めるべき遷移確率が4つで、条件が3つしかないので、このままでは一意に決めることができない。そこで適当に決めることにする。その代表的な方法がメトロポリス法と熱浴法である。
熱浴法
詳細釣り合い条件は
$$
\exp(-\beta E_A) P(A \rightarrow B) = \exp(-\beta E_B) P(B \rightarrow A)
$$
と書かれるのだから、$P(A \rightarrow B)$や$P(B \rightarrow A)$がそれぞれ$\exp(-\beta E_B)$、$\exp(-\beta E_A)$に比例するように取るのが自然であろう。そこでこのように決める。
$$
P(A \rightarrow B) = \frac{\exp(-\beta E_B)}{\exp(-\beta E_A)+\exp(-\beta E_B)}
$$
$$
P(B \rightarrow A) = \frac{\exp(-\beta E_A)}{\exp(-\beta E_A)+\exp(-\beta E_B)}
$$
これを熱浴法(Heatbath method)と呼ぶ。
メトロポリス法
詳細釣り合い条件は、遷移確率の比を指定するものであった。なので、遷移確率のうち大きい方を1にとってしまおう。いま、$E_A < E_B$とすると、$P(A \rightarrow B) < P(B \rightarrow A)$となる。なので$P(B \rightarrow A) = 1$とすると、詳細釣り合い条件から、
$$
P(A \rightarrow B) = \frac{\exp(-\beta E_B)}{\exp(-\beta E_A)} = \exp(-\beta \Delta E)
$$
となる。ただし$\Delta E = E_B - E_A$である。
これは、教科書ではよく「エネルギーが下がる方向には確率1で遷移、エネルギーが上がる方向にはそのエネルギー差を$\Delta E $として確率$\exp(-\beta \Delta E)$で遷移」と説明されるので、エネルギーの下がる方向には行きやすく、エネルギーが上がる向きには行きにくいことを表現云々と理解されることが多く、それは間違ってはいないのだが、実際には単に「詳細釣り合いを満たしつつ、大きい方の遷移確率を1にとった」と理解するほうが誤解が無いように思う。
詳細釣り合いと収束
先程詳細釣り合い条件を導出する際は、「ボルツマン重みに比例する状態を平衡状態として持つこと」を要請した。すなわち必要条件のように見える。しかし、詳細釣り合い条件を満たす系は、状態遷移を繰り返すと、希望する平衡状態に必ず収束することが証明できる4。証明は教科書に書いてあるのでここでは紹介しない。詳しくは参考文献を参照のこと。
ここではいくつかの系で、詳細釣り合い条件を満たすように作られた遷移確率で系を時間発展させると、確率分布が希望する平衡状態に収束することを示す。
三状態の系
状態A, B, Cを持つ系を考える。それぞれエネルギーは$E_A, E_B, E_C$とし、$E_A < E_B < E_C$としておく。
今後のため、
\begin{align}
a &= \exp(-\beta E_A) \\
b &= \exp(-\beta E_B) \\
c &= \exp(-\beta E_C) \\
Z &= a + b + c
\end{align}
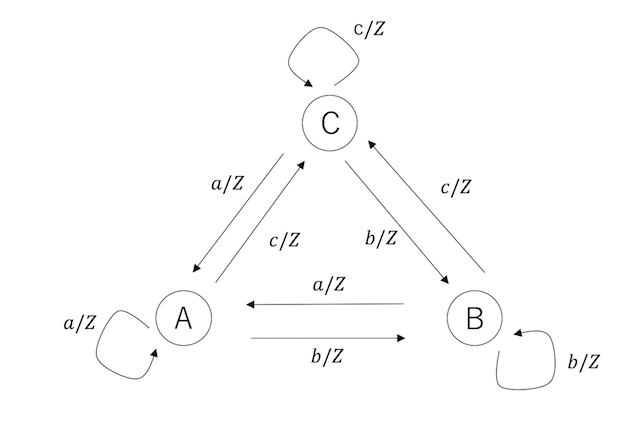
と表記しておこう。まず、熱浴法を用いた場合の遷移確率は以下のようになる。
要するに状態Aに向かう矢印は$a/Z$、Bに向かう矢印は$b/Z$などとなる。この遷移行列を書いてみよう。時刻tに置いて状態Aにいる確率を$\pi_A(t)$などと表記すると、遷移行列はこう書ける。
\begin{pmatrix}
\pi_A(t+1) \\
\pi_B(t+1) \\
\pi_C(t+1)
\end{pmatrix}
=
\begin{pmatrix}
a/Z & a/Z & a/Z \\
b/Z & b/Z & b/Z \\
c/Z & c/Z & c/Z \\
\end{pmatrix}
\begin{pmatrix}
\pi_A(t) \\
\pi_B(t) \\
\pi_C(t)
\end{pmatrix}
こいつをMathematicaに突っ込んで固有値と固有ベクトルを求めてみよう。
In[39]:= Z := a + b + c
In[40]:= Eigensystem[{{a/Z, a/Z, a/Z}, {b/Z, b/Z, b/Z}, {c/Z, c/Z,
c/Z}}]
Out[40]= {{0, 0, 1}, {{-1, 0, 1}, {-1, 1, 0}, {a/c, b/c, 1}}}
要するに固有値は1と0(縮退)で、固有値1に対応する固有ベクトルは$(a,b,c)$であることがわかる。実際に、詳細釣り合いを満たすように作られた遷移行列は、必ず最大固有値$1$を持ち、かつそれに対応する固有ベクトルが平衡状態であることが示される。
行列を何度もかけていった時の最大固有値に対応するベクトルへの収束は、最大固有値と第二最大固有値の絶対値の比で決まるが、三状態で熱浴法の場合には第二固有値が0なので一発で収束することがわかる(現在の状態に関係なく次の状態をボルツマン重みに従って選んでるので当然だが・・・)。
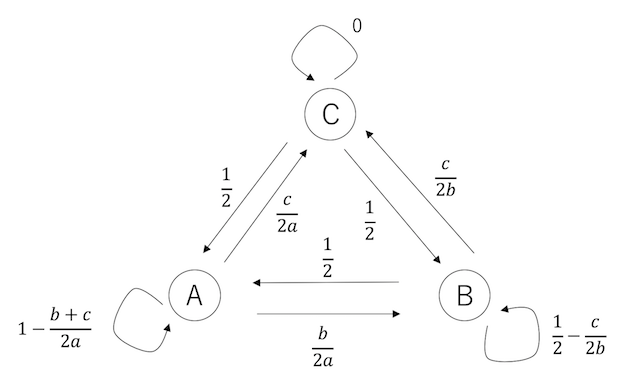
次にメトロポリス法を考える。メトロポリス法では、まず遷移先を当確率で選び、次にそこに遷移するかどうかを決める。遷移図はこんな感じ。
例えばいま状態Bにいる場合、確率1/2でAに行こうとするかBに行こうとするか決める。Aに決まった場合は確率1で遷移するので、Aに行く確率は1/2。Cに決まった場合は確率$c/b$で遷移するのでCに行く確率は合わせて$c/2b$。そうやって遷移確率を決めていくと上図が得られる。
こいつをMathematicaに突っ込んでみよう。
In[42]:= Eigensystem[{{1 - (b + c)/2/a, 1/2, 1/2}, {b/2/a,
1/2 - c/2/b, 1/2}, {c/2/a, c/2/b, 0}}]
Out[42]= {{1, -(c/(2 b)), -((-a + b + c)/(2 a))}, {{a/c, b/c,
1}, {0, -1, 1}, {-((b + c)/c), b/c, 1}}}
最大固有値が1で、対応する固有ベクトルが$(a,b,c)$になるのは同じ。ただし今回は第二固有値が0ではないので、収束には有限の時間がかかる。
四状態の系
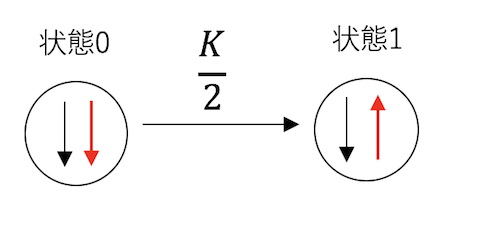
三状態の系では(特に熱浴法が)あまりに自明すぎるので、四状態の系を考える。イジングスピン二個の系で、相互作用は強磁性的で、かつ外場無しとしよう。スピンが揃った状態のエネルギーを基準とし、スピンが反対向きの場合のエネルギーを$\Delta E$とする。後のために
$$
K = \exp(-\beta \Delta E)
$$
としておこう。
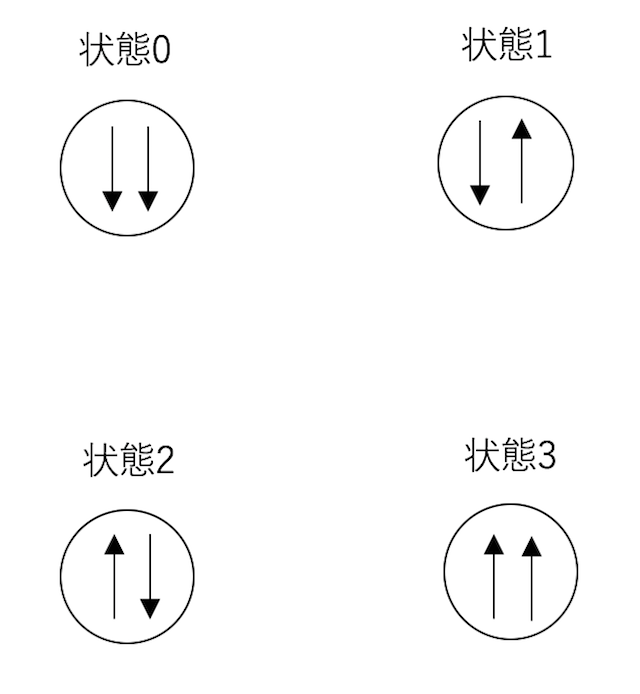
スピンの状態をビットだと思って、それぞれ状態0から状態3まで名前をつける。
熱浴法
まず、熱浴法を考えよう。状態0から状態1に遷移するためには
- 右のスピンが選ばれ
- かつ上向きの状態を選ぶ
必要がある。いまは下向きが揃った状態でエネルギーが低いため、下向きの状態の重みが$1$、上向きの重みが$K$となる。熱浴法では遷移確率は$K/(1+K)$となる。右のスピンが選ばれる確率は1/2であるから、状態0から状態1に行く確率は合わせて$K/2(1+K)$となる。
同様にして全ての確率を決めることができる。手で全部計算しても良いが間違えそうなのでスクリプトにやらせよう。
print "{"
4.times do |j|
print "{"
4.times do |i|
if i==j
if i==0 or i == 3
print "1/(1+K)"
else
print "K/(1+K)"
end
else
if (~i&3)==j
print "0"
else
if i==0 or i==3
print "K/(1+K)/2"
else
print "1/(1+K)/2"
end
end
end
print "," if i !=3
end
print "}"
print "," if j !=3
end
print "}"
puts
実行結果をMathematicaに食わす。
In[43]:= Eigensystem[{{1/(1 + K), 1/(1 + K)/2, 1/(1 + K)/2,
0}, {K/(1 + K)/2, K/(1 + K), 0, K/(1 + K)/2}, {K/(1 + K)/2, 0,
K/(1 + K), K/(1 + K)/2}, {0, 1/(1 + K)/2, 1/(1 + K)/2, 1/(1 + K)}}]
Out[43]= {{1/(1 + K), 0, K/(1 + K),
1}, {{-1, 0, 0, 1}, {1, -1, -1, 1}, {0, -1, 1, 0}, {1, K, K, 1}}}
最大固有値が1、対応する固有ベクトルが$(1, K, K, 1)$であることがわかる。第二固有値は$1/(1+K)$で、これが収束の早さを決める。
メトロポリス法
メトロポリス法も簡単である。まず、右か左のスピンをランダムに選び、次にそのスピンをひっくり返したエネルギーを計算し、エネルギーが下がる向きには必ず遷移、そうでない場合はボルツマン重みで遷移確率を決める。
例えば状態0から状態1への遷移は、右のスピンが選ばれる確率が$1/2$、それがひっくりかえる確率が$K$であるから、合わせて$K/2$となる。こうして全ての遷移確率を決めることができるが、やっぱり面倒なのでスクリプトにやらせよう。
print "{"
4.times do |j|
print "{"
4.times do |i|
if i==j
if i==0 or i == 3
print "1-K"
else
print "0"
end
else
if (~i&3)==j
print "0"
else
if i==0 or i==3
print "K/2"
else
print "1/2"
end
end
end
print "," if i !=3
end
print "}"
print "," if j !=3
end
print "}"
puts
これをMathematicaに食わすとこんな感じ。
In[44]:= Eigensystem[{{1 - K, 1/2, 1/2, 0}, {K/2, 0, 0, K/2}, {K/2, 0,
0, K/2}, {0, 1/2, 1/2, 1 - K}}]
Out[44]= {{1, 0,
1 - K, -K}, {{1, K, K, 1}, {0, -1, 1, 0}, {-1, 0, 0, 1}, {1, -1, -1,
1}}}
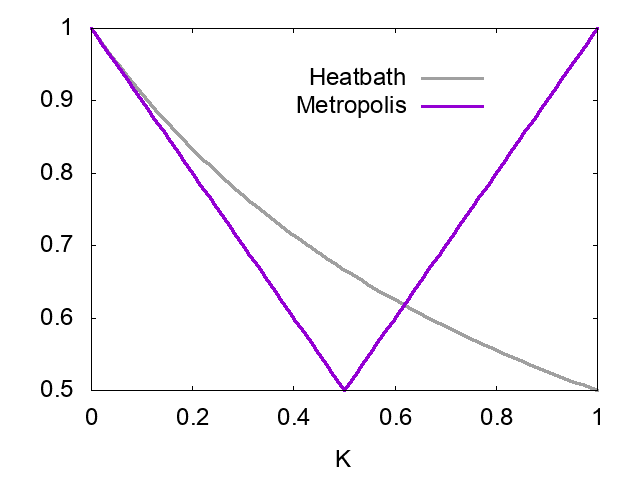
最大固有値が1で、対応する固有ベクトルが$(1,K,K,1)$なのは同じだが、第二固有値の絶対値は$K$か$1-K$の大きい方となる。
図示するとこんな感じ。
要するに$K=(\sqrt{5}-1)/2 \sim 0.62$くらいまではメトロポリス法の方が第二固有値が小さいのが、それより大きな$K$では熱浴法の方が固有値が小さくなる。
まとめ
マルコフ連鎖モンテカルロ法における詳細釣り合い条件と熱浴法、メトロポリス法の確率の決め方を見てみた。詳細釣り合い条件と確率の保存則だけでは遷移確率が決まらないので、新たに追加する条件が熱浴法やメトロポリス法である。無論、遷移確率の比が詳細釣り合いを満たしていれば何をしても良いので、例えば無駄に自分自身に戻る確率を増やしても収束が遅くなるだけで平衡状態は変わらない。
具体的な系において遷移行列を書いてみると、ちゃんと最大固有値が1となり、対応するベクトルが平衡状態になっていることがわかる。収束の早さは第二固有値の絶対値で決まるが、熱浴法とメトロポリス法のどちらが早いかは系や条件(温度)に依る。っていうかそういう先行研究はどうせ数十年ほど前に死ぬほどやられてるだろうから興味がある人は調べて見られたい。
参考文献
- J. Gurbernatis, N. Kawashima, and P. Werner "Quantum Monte Carlo Methods", Cambridge University Press. 量子モンテカルロの本だが、古典モンテカルロ法の詳細釣り合い条件や、収束の証明などが平易に書いてある。