【統計学】マルコフ連鎖モンテカルロ法(MCMC)によるサンプリングをアニメーションで解説してみる。

Pythonでマルコフ連鎖モンテカルロ法を実装して解説してみる記事です

『計算統計 II マルコフ連鎖モンテカルロ法とその周辺』のp16に

この節の内容を実感するために一番良い方法は、どんな計算機言語でもいいから、
ここで述べたことを白紙から実装してみることである。

という事で、素直にやってみました。せっかくなのでコードと仕組みの解説をしようと思います。

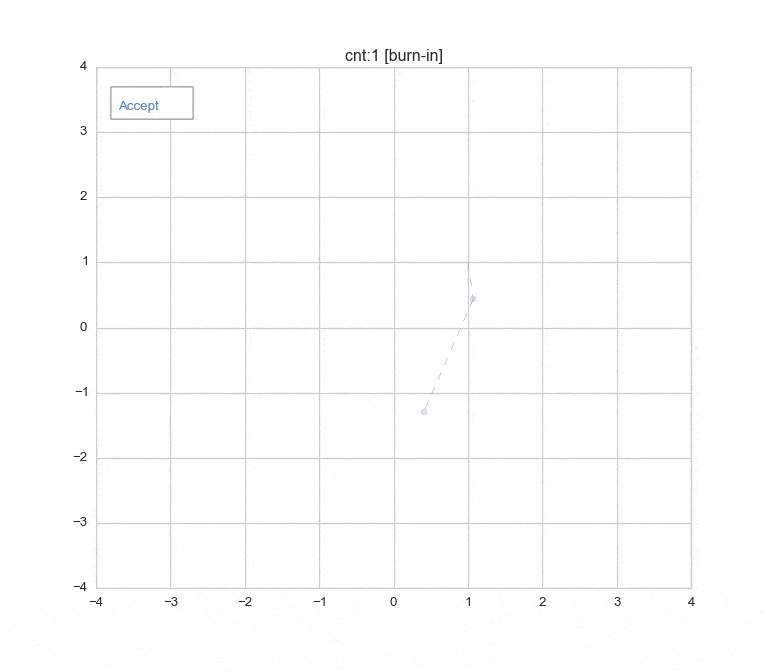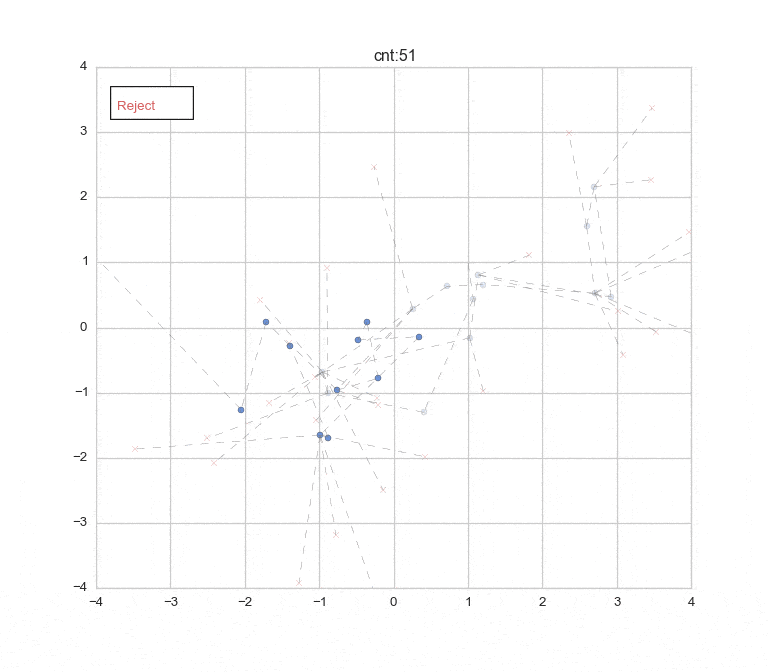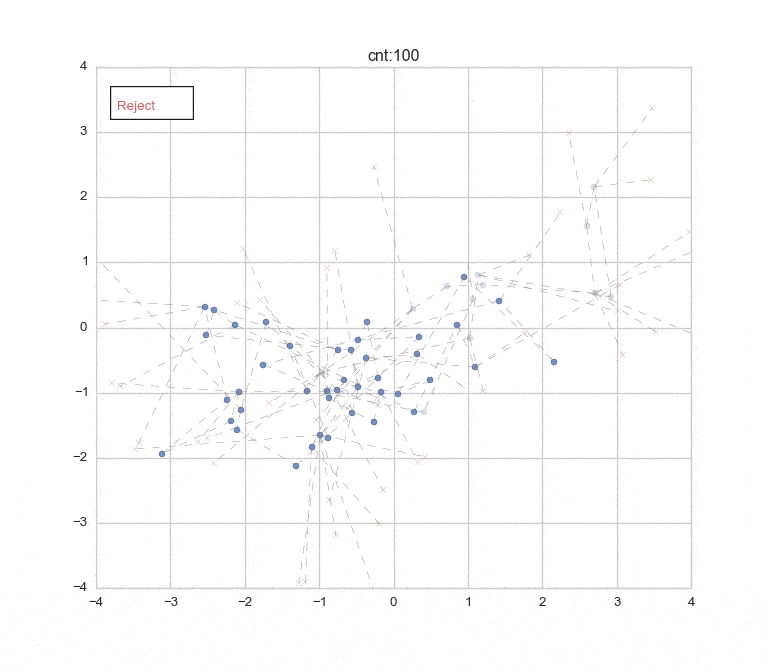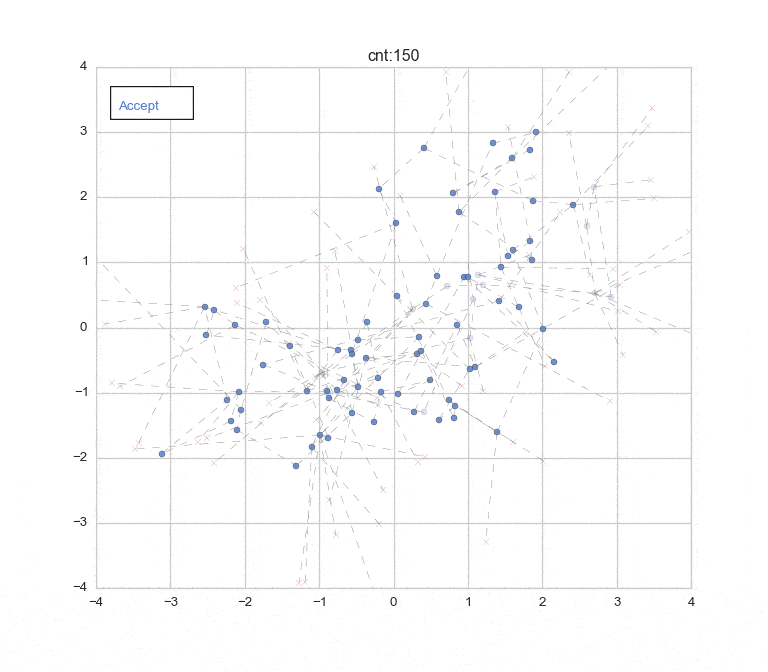
先に結果のアニメーションとプロットを表示しておきます
(Burn-in期間：1-30 [この期間のデータは色を薄くしてプロットしています。], 棄却含め150回のサンプリングまで)

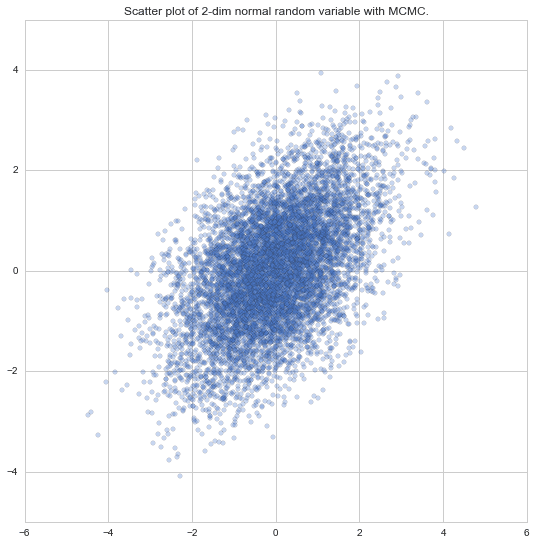
10,000回繰り返してサンプリングした結果をプロット。（うち、Burn-in: 2,000回）

はじめに

まず最初に必要なライブラリのインポートを行います。

import numpy as np
import numpy.random as rd
import pandas as pd
import scipy.stats as st
import copy

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import animation as ani
import matplotlib.cm as cm
import seaborn as sns
sns.set(style="whitegrid", palette="muted", color_codes=True)

##今回サンプリングの対象とする目標分布 (Target Distribution)

f(x,y) = {\sqrt{1-b^2} \over 2\pi } \exp \left( -{1 \over 2} (x_1^2 - 2bx_1x_2 + x_2^2)  \right) \\
\propto \exp \left( -{1 \over 2} (x_1^2 - 2bx_1x_2 + x_2^2)  \right) \\

2次元正規分布から正規化定数を除いたものを使います。この分布の中で、確率密度の比較をするので、定数部分は無視して構わないのです。PythonでP(・)という関数を定義してこれをこの目標分布とします。

# 目標分布：２次元正規分布の確率密度関数から正規化定数を除いたもの
def P(x1, x2, b):
    assert np.abs(b) < 1
    return np.exp(-0.5*(x1**2 - 2*b*x1*x2 + x2**2))

各種パラメーターを定義します。

# parameters
b = 0.5            # 対象分布の共分散
delta = 1          # 提案分布の標準偏差
dist_type = "norm" # 提案分布の種別("norm" or "unif")
print "提案分布の種別:", dist_type

num_frame = 150.   # アニメーションのトータルフレーム数

# サンプリング結果を格納するリスト
sample = []
# 1:accept, 0:rejectを格納するリスト
acc_rej = [] 

パラメーターを設定したところで、サンプリングを行いアニメーションの描画をする処理に入ります。
要所要所に解説コメントを入れました。

# 初期位置の設定とサンプリング結果リストへの格納
current = (3, 3)
sample.append(current)

# アニメーションの各フレームを描画する関数
def animate(nframe):
    global current, acc_rej
    print nframe,       # 進捗状況の表示

    # 提案分布による次のステップの選択
    # dist_type: "norm":正規分布 / "unif"：一様分布
    if dist_type == "norm":
        next = (current[0] + rd.normal(0, delta), current[1] + rd.normal(0, delta))
    else:
        next = (current[0] + rd.uniform(-delta, delta), current[1] + rd.uniform(-delta, delta))
    # 各位置における目標分布の確率密度の比・・・[[1]]
    P_prev = P(current[0], current[1], b)   # 現在位置における目標分布の確率密度(に比例した数値)
    P_next = P(next[0], next[1], b)         # 次の候補位置における目標分布の確率密度(に比例した数値)

    # 上記の２つの値の比をとる
    r = P_next/P_prev
    
    # グラフの左上にAccept / Reject を表示する枠を表示
    ax = fig.add_subplot(111)
    rect = plt.Rectangle((-3.8,3.2), 1.1, .5,fc="#ffffff", zorder=nframe)
    ax.add_patch(rect)
    
    # 現在位置から次の候補位置への移動パスを表す点線を引く
    plt.plot([current[0], next[0]], [current[1], next[1]], "k--", lw=.3, color="gray") 
    
    if r > 1 or r > rd.uniform(0, 1):     # ・・・[[2]]
        # 0-1の一様乱数がrより大きい時は状態を更新する。 
        current = copy.copy(next)
        # サンプリングした値をリストに詰める。
        sample.append(current) 
        
        if nframe < num_frame*.2:
            # イテレーション回数の最初の20%はBurn-in期間と考える(プロットの色を薄くして示す）
            alpha = 0.2
        else:
            # 通常期間は点の濃さを戻す
            alpha = 0.8
            # acceptを記録
            acc_rej.append(1)
            
        # 採択(Accept)なので、点をプロットする。
        plt.scatter(current[0], current[1], alpha=alpha)
        plt.text(-3.7, 3.35, "Accept", zorder=nframe, fontdict={'color':"b"})
        
    else:  
        # 0-1の一様乱数がrより小さい時は棄却する。 
        # 棄却した時は x印をプロットする。
        plt.scatter(next[0], next[1], alpha=0.5, color="r", marker="x")
        plt.text(-3.7, 3.35, "Reject", zorder=nframe, fontdict={'color':"r"})
        
        if nframe <= num_frame*.2:
            # rejectを記録
            acc_rej.append(0)

    if nframe >= num_frame*.2:
        plt.title("cnt:{}".format(nframe+1))
    else:
        plt.title("cnt:{} [burn-in]".format(nframe+1))

    # グラフの描画範囲の設定
    plt.xlim(-4, 4)
    plt.ylim(-4, 4)
    

fig = plt.figure(figsize=(8,7))
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('metropolis_norm.gif', writer='imagemagick', fps=3, dpi=96)

# 採択(Accept)率の計算
print "Accept ratio:{0:.5f}".format(np.mean(acc_rej))

採択率は 約60%でした。あまり高くないですね

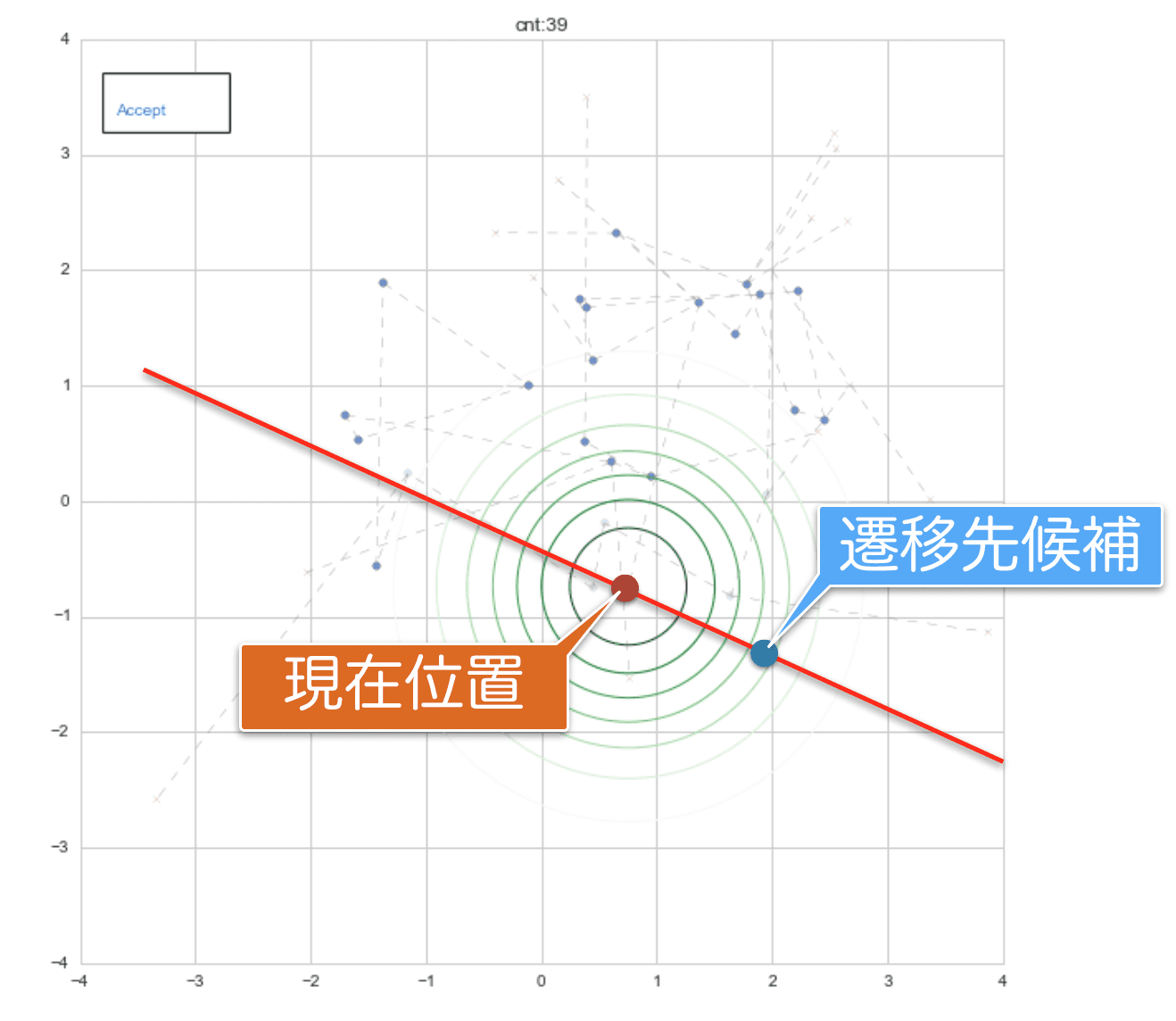
このメトロポリスヘイスティングス法は、各サンプリング時に提案分布によって次の遷移先を選んでいます。下記は40回目のサンプリングまで実行した時に、その次を選ぶための提案分布をその確率密度に応じて等高線で表したものです。赤い点が現在位置です。
いま提案分布から得られる次の候補点を

x_1^{(t+1)} = x_1^{(t)} + N(0, 1) \\
x_2^{(t+1)} = x_2^{(t)} + N(0, 1) 

としているので、このような等高線が描けています。この提案分布は現在位置によらず、$N(0, 1)$に従い１つ値をランダムに生成するので、例えば下記図のように、目標分布の確率密度の低い方向に次の遷移先を選択することもあります。

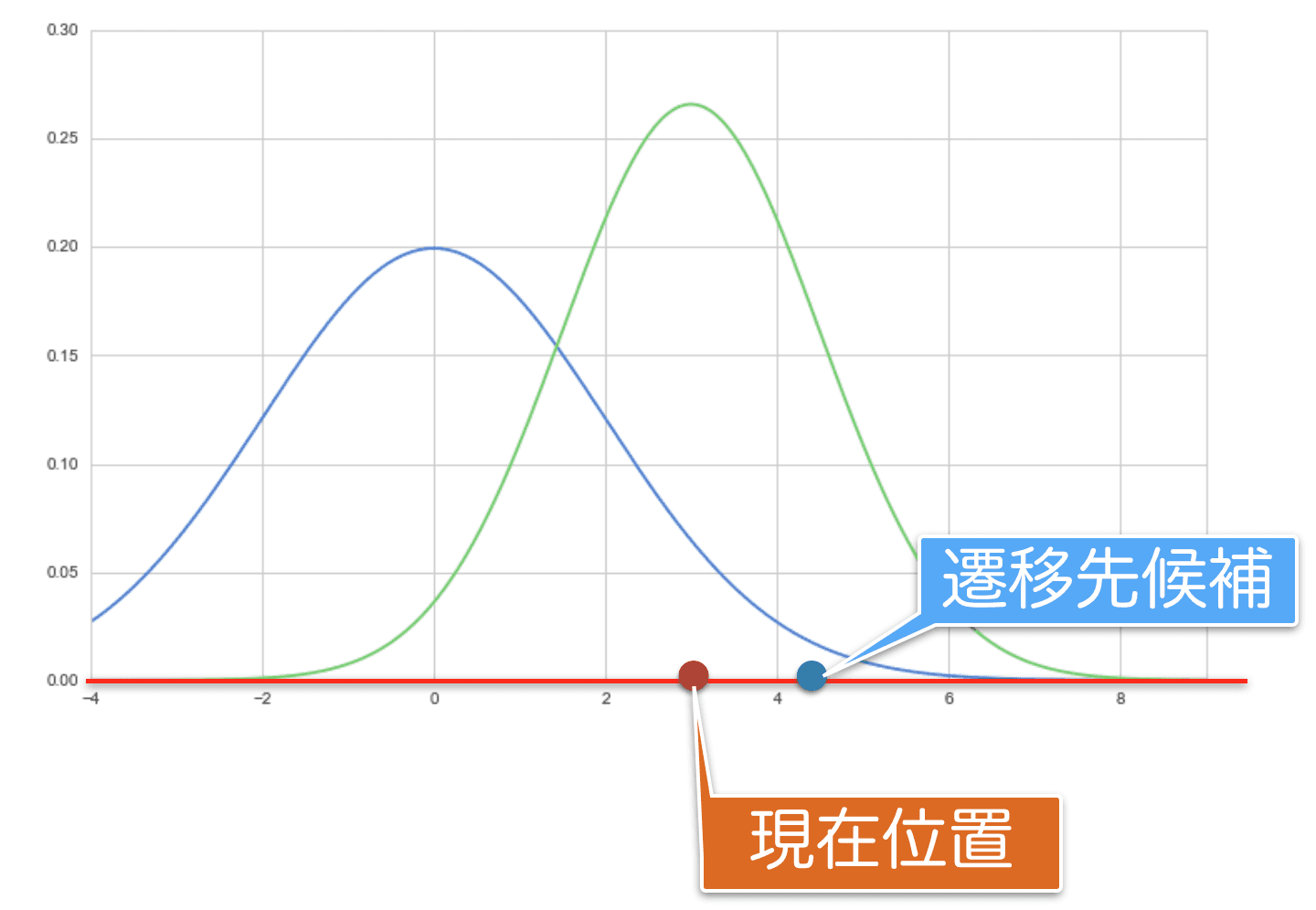
上図の赤い線に沿ってすっぱり縦に切ってみた時の断面のイメージが下記です。青線が目標分布で、緑線が提案分布です。いま、中央が現在位置となる提案分布から乱数が生成され、青い点が遷移先の候補として選択されています。

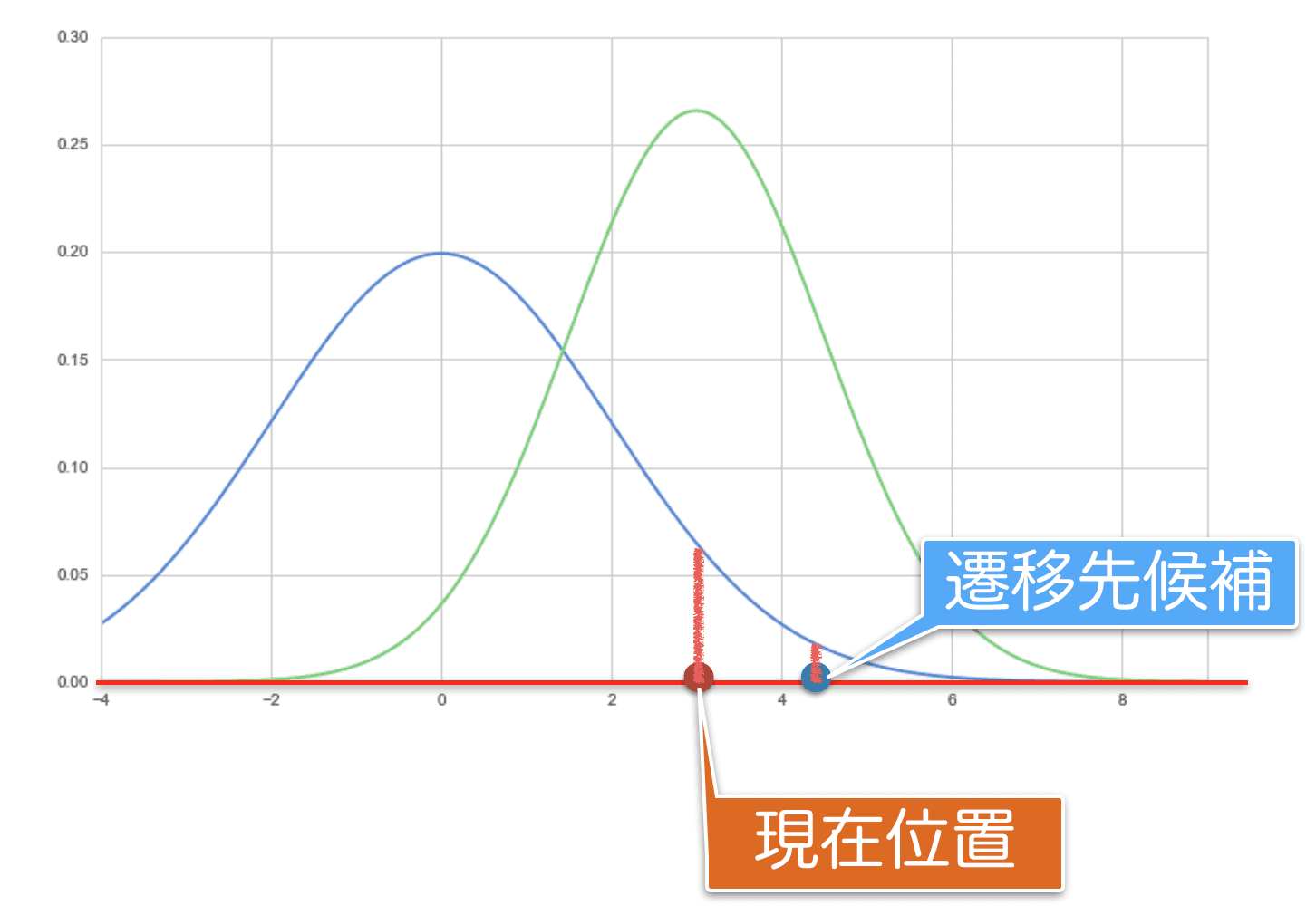
さてこの「現在位置における目標分布の確率密度」と「遷移先候補における目標分布の確率密度」を比べてみたいと思います。下記のピンクの２本の線がそれぞれ該当します。直感的には今回の遷移先の候補は目標分布に照らし合わせると、確率密度の低い場所なので、滅多に実現しないはずと考えられます。いま、提案分布からの乱数を使っているので、その目標分布の確率密度が考慮されていない状態なのです。
その目標分布の確率密度を反映するために、この遷移先候補はある一定のルールに基づき採択(Accept)、棄却(Rejet)をすることによって、反映することを考えます。

比をとって比べてみます。その比を$r$とすると、

と表せます。Pythonコード上は

    # 各位置における目標分布の確率密度の比・・・[[1]]
    P_prev = P(current[0], current[1], b)   # 現在位置における目標分布の確率密度(に比例した数値)
    P_next = P(next[0], next[1], b)         # 次の候補位置における目標分布の確率密度(に比例した数値)
    # 上記の２つの値の比をとる
    r = P_next/P_prev

の部分です。

この$r$は0以上の数値をとります。この比がある種の採択確率であると解釈をして採択ルールを決めます。

まず$r \ge 1$の場合は必ず採択されるとします。

$0 \le r < 1$の場合は、[0,1]の一様乱数と比べることで、$r$の値が採択確率と見なせるよう処理を行います。

今回のPythonコードでは、

    if r > 1 or r > rd.uniform(0, 1):     # ・・・[[2]]
        …

の部分が対応しています。

これを繰り返すことで、目標分布に対するサンプリングを行うことができます。これがうまくいくことの理論的な裏付けは『計算統計 II マルコフ連鎖モンテカルロ法とその周辺』をご参照ください。

10,000個のサンプリング実行

上記のアニメーションは150個のサンプリングと数が少なかったので、10000個のサンプリングを行い、より目標分布が見えるようにプロットしてみます。

# parameters
b = 0.5
delta = 1
dist_type = "norm" # "norm" # "unif"
n_samples = 10000

# result
sample = []

#initial state
current = (5, 5)
sample.append(current)

print dist_type

cnt = 1
while cnt < n_samples:
    # candidate of next step
    if dist_type == "norm":
        next = (current[0] + rd.normal(0, delta), current[1] + rd.normal(0, delta))
    else:
        next = (current[0] + rd.uniform(-delta, delta), current[1] + rd.uniform(-delta, delta))

    P_prev = P(current[0], current[1], b)
    P_next = P(next[0], next[1], b)

    r = P_next/P_prev

    if r > 1 or r > rd.uniform(0, 1):
        # 0-1の一様乱数がrより大きい時は状態を更新する。 
        current = copy.copy(next)
        sample.append(current)
        cnt += 1
    
sample = np.array(sample)
plt.figure(figsize=(9,6))
plt.scatter(sample[int(len(sample)*0.2):,0], sample[int(len(sample)*0.2):,1], alpha=0.2)
plt.title("Scatter plot of 2-dim normal random variable with MCMC.")
plt.show()

分散共分散行列が

[[1,  0.5],
 [0.5,  1]]

の正規分布となっていそうに見えるプロットとなりました

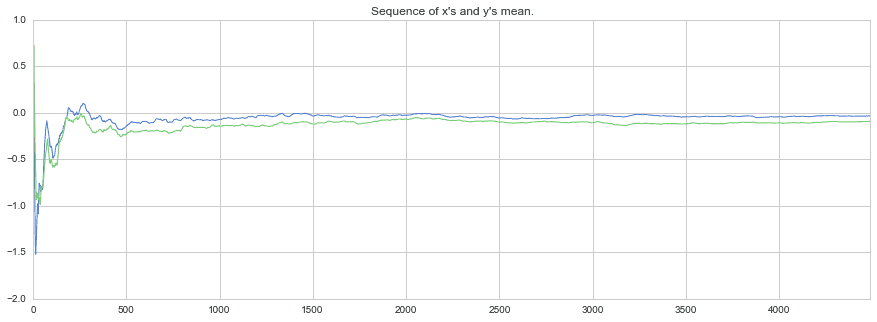
平均値の推移

$x_1$、$x_2$のサンプリングをしている間の平均値の推移も見てみます。徐々に想定通りの平均値:0に近づいている様子が伺えます。ちょうど平均値が0になってきたところで10000個(burn-in 2000個含む)に達してしまったので、もう少しサンプリング数を増やしてもいいかもしれないですね。

ave = [[],[]]

start = len(sample) * 0.2
for i, d in enumerate(np.array(sample[int(start):])):
    #print d
    for j in range(2):
        if i == 0:
            ave[j].append(float(d[j]))
        else:
            ave[j].append( (ave[j][i-1]*i + d[j])/float(i+1) )


plt.figure(figsize=(15, 5))
plt.xlim(0, len(sample[int(start):]))
plt.plot(np.array(ave).T, lw=1)
plt.title("Sequence of x's and y's mean.")
plt.show()

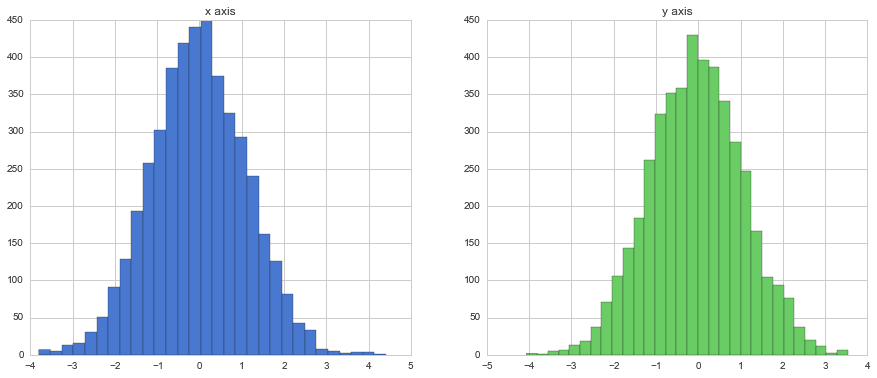
サンプリング結果のヒストグラム

fig = plt.figure(figsize=(15,6))

ax = fig.add_subplot(121)
plt.hist(sample[start:,0], bins=30)
plt.title("x axis")

ax = fig.add_subplot(122)
plt.hist(sample[start:,1], bins=30, color="g")
plt.title("y axis")

plt.show()

コード一式

本記事で使用したコードはGithubのこちらに置いてあります。

参考

『計算統計 II マルコフ連鎖モンテカルロ法とその周辺』第I部「マルコフ連鎖モンテカルロ法の基礎」（伊庭幸人）
　　https://www.iwanami.co.jp/.BOOKS/00/0/0068520.html

可視化で理解するマルコフ連鎖モンテカルロ法(MCMC)
　　http://d.hatena.ne.jp/hoxo_m/20140911/p1
　　⇒ @hoxo_m おやぶんがすでに同じようなアニメーションをブログに書いていました・・・。
　　　２番煎じですみません・・・。

MacでPythonからアニメーションGIFを生成する環境設定
　　http://qiita.com/kenmatsu4/items/573ca0733b192d919d0e