JavaScriptで重複排除を自分で実装してはいけない（Setを使う）

若者とプログラミングをしていて非常にショックを受けたのだが「JavaScript 配列 重複 削除」で検索するとfilterとindexOfを使ったアルゴリズムが検索結果上位に出てくる。これはO(N^2)。計算量の概念がないというのはとても恐ろしい。Big Techがアルゴリズム偏重の試験を課すのは合理的だと確信した。

— 父🌒 (@fushiroyama) March 10, 2020

先日このようなツイートが流れてきたので、$O(N^2)$、つまり計算量が $N^2$ に比例するということの恐ろしさを簡単に書きます。

JavaScriptで配列から重複を排除するコード

EcmaScript 2015から導入されたSetを使えばものすごく簡単に書けます。

const array1 = [1, 5, 3, 1, 5, 3];
const array2 = Array.from(new Set(array1))
console.log(array2); // [ 1, 5, 3 ]

文字列でももちろん問題ありません。

const array1 = ["A", "D", "C", "A", "D", "C"];
const array2 = [...new Set(array1)];
console.log(array2); // [ "A", "D", "C" ]

~~順序は保証されないので、~~必要に応じてソートしたりしてください。
[2020/4/29修正] 順序は要素を投入した順が保持されます。@righteousさんご指摘ありがとうございました！

アルゴリズム、重要！

古いコードを検証する

最初に引用したツイートの通り、適当に検索をかけると未だに次のようなコードがたくさんヒットします。

const result = array.filter((x, i) => array.indexOf(x) === i)

これはまず何をやっているのか直感的に分からないという問題があるのですが、計算量の点でも困ったことがあります。
たとえば元となる配列が [1, 2, 3, ..., N] という重複なしの連番だったとしましょう。するとこの filter() は

1. 1 を全配列の中から探し、インデックス 0 を得る → true を返す
2. 2 を全配列の中から探し、インデックス 1 を得る → true を返す
3. ……

という処理を配列の全ての要素に対して行います。それぞれの処理はNに比例した回数の比較を行う必要があります¹。それが配列の最初から最後までN回繰り返されるわけですから、つまりこの処理は$O(N^2)$、配列のサイズの2乗に比例した計算量を要することになります²。データ量が10倍なら計算量は100倍、データ量が100倍なら計算量は10,000倍です。「一瞬待つけどいいか」と思って実装したら後からデータ量が10倍になって大変なことになったりします³。

改善策は？

まず簡単に思い付く案として、配列を事前にソートしておくことにしたらどうでしょうか。クイックソートの計算量は $O(N logN)$ ですが、その後で隣同士の要素が異なるものだけを残すという処理を行えばあっという間に重複排除は終了します。$O(N^2)$との差は要素数が増えるにしたがってどんどん拡大していきます。

また、ベストな選択肢は冒頭に書いたSetを使う方法でしょう。こちらはJavaScriptのエンジンに直接搭載された機能なので、素人がJavaScriptのコードをこねまわすよりはるかに高速な結果が期待できます。

速度比較

というわけで、実際にコードを書いて速度を比較します。

検証コード＆実行環境

検証コード

// 0～(N-1)までの数を(N*100)個ランダムに作って配列に詰める
const generate = (N) => {
  const nums = [];
  for (let i = 0; i < N*100; i++) {
    nums.push(Math.floor(Math.random() * N));
  }
  return nums;
}

// (1) filter()を使って重複を排除する
const test1 = (nums) => {
  const result = nums.filter((num, i) => nums.indexOf(num) === i);
  return result;
}

// (2) sort()してから隣同士同じものを排除する
const test2 = (nums) => {
  nums.sort();
  const result = [];
  for(let i = 0; i < nums.length; i++) {
    if (i === 0) { result.push(nums[i]); }
    else if (nums[i-1] !== nums[i]) { result.push(nums[i]); }
  }
  return result;
}

// (3) Setを使う
const test3 = (nums) => {
  const result = Array.from(new Set(nums));
  return result;
}

• Windows 10 Professional
• Core i7-8700K
• Chrome 81.0.4044.129
• 実行時間は5回平均で算出

| 要素数 | (1) filter()を使う | (2) sort()を使う | (3) Setを使う |
|-------------+-------------------|------------------|--------------|
| 100,000 | 88ms | 26ms | 1.6ms |
| 1,000,000 | 8,737ms | 314ms | 17ms |
| 10,000,000 | 870,897ms⁴ | 3,815ms | 276ms |
| 100,000,000 | （省略） | 44,268ms | 4,783ms |

(1), (2), (3)とそれぞれ比較するのがアホらしくなるほど桁が違う結果が得られました。これはアルゴリズムの違いもありますが、JavaScriptエンジンに搭載されたネイティブなコードで動いている⁵という違いもあるでしょう。

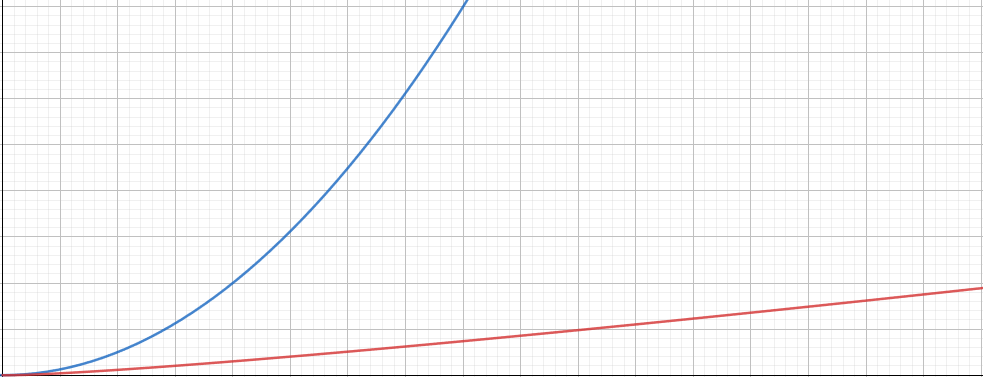
また増え方にも注目しましょう。(1)では要素数を10倍増やすごとに愚直に100倍時間が増えていますが、(3)では要素数が10倍になっても時間は16～17倍しか増えていません。これが $O(N^2)$ の恐ろしさです。

結論

世の中には、

• 計算量を特に気にしなくてもいい場面
• 計算量がクリティカルになる場面
• 計算量を気にしなくていいと思っていたらいつの間にか大変なことになる場面

があります。せっかく高速なアルゴリズムがパッケージされてすぐ手の届くところに用意されているのですから積極的に活用していきたいものです。

1. 平均してN/2回の比較を行う必要があります ↩

2. この例だと合計N(N+1)/2回の比較を行うことになります ↩

3. フロントエンドでここまで多数の要素を扱うことは稀だとは思いますが…… ↩

4. 時間がかかるのでここは1回だけ ↩

5. 我々よりも賢い人たちが多大な労力をかけてC++で実装したという意味です ↩