分離超平面定理と衝突判定

次のようなアルゴリズムの問題について考えてみましょう.

問題
平面上に赤い点が$n$個と青い点が$m$個あり, それぞれの色の点によって2つの凸多角形が定義されている. これら$n+m$の点の座標を入力とし, 図形同士が重なっているかどうか判定するアルゴリズムを構築せよ.

これはゲームプログラミングにおいて, ゲームオブジェクト同士の衝突を判定するために重要なアルゴリズムです.

準備運動: 一次元の場合

今, 数直線上に2つの閉区間$A$と$B$があるとします. これらが重なっていないというのは, 間に点を置いて分離できるということです. つまり, 次のことが自明に成り立ちます.

$A$ と $B$ が重なっていなくて $A$ が小さい方にあるならば, ある点 $c$ が存在し, 任意の $a \in A$ に対し, $a < c$ かつ 任意の $b \in B$ に対し $c < b$

あたりまえですね. では, $A$と$B$の左右関係が不明な場合はどうしたらいいでしょうか? この問題に対応するために, 必要に応じて数直線を反転するようにしましょう.

$A$ と $B$ が重なっていないならば, ある方向 $v \in \{ -1, +1 \}$ とある点 $c$ が存在し, 任意の $a \in A$ に対し, $av < c$ かつ任意の $b \in B$ に対し $c < bv$

$A$ が小さい方にあるなら, $v=+1$として元の命題のままになり, $A$が大きい方にあるなら $v=-1$とすることで, 無理やり $A$の方を$<c$, $B$の方を$c<$で保っています.

ところで, 閉区間の中にあるすべての点を走査するのは大変そうです. よく見ると $A<B$のときは$A$の最大値と$B$の最小値, $A>B$のときは$A$の最小値と$B$の最大値のみを確認すれば十分だということが分かります. つまり最大値や最小値の候補になる両端だけ調べれば十分と言えます.

...... と色々考察しましたが, 実際に計算するには分離するための点 $c$ なんか計算しなくても次のように判定できます.

def is_intersect_1d(A, B):
    return A[0] <= B[1] and B[0] <= A[1]

if __name__ == "__main__":
    print(is_intersect_1d([1, 2], [3, 4])) # False
    print(is_intersect_1d([1, 3], [2, 4])) # True
    print(is_intersect_1d([1, 4], [2, 3])) # True

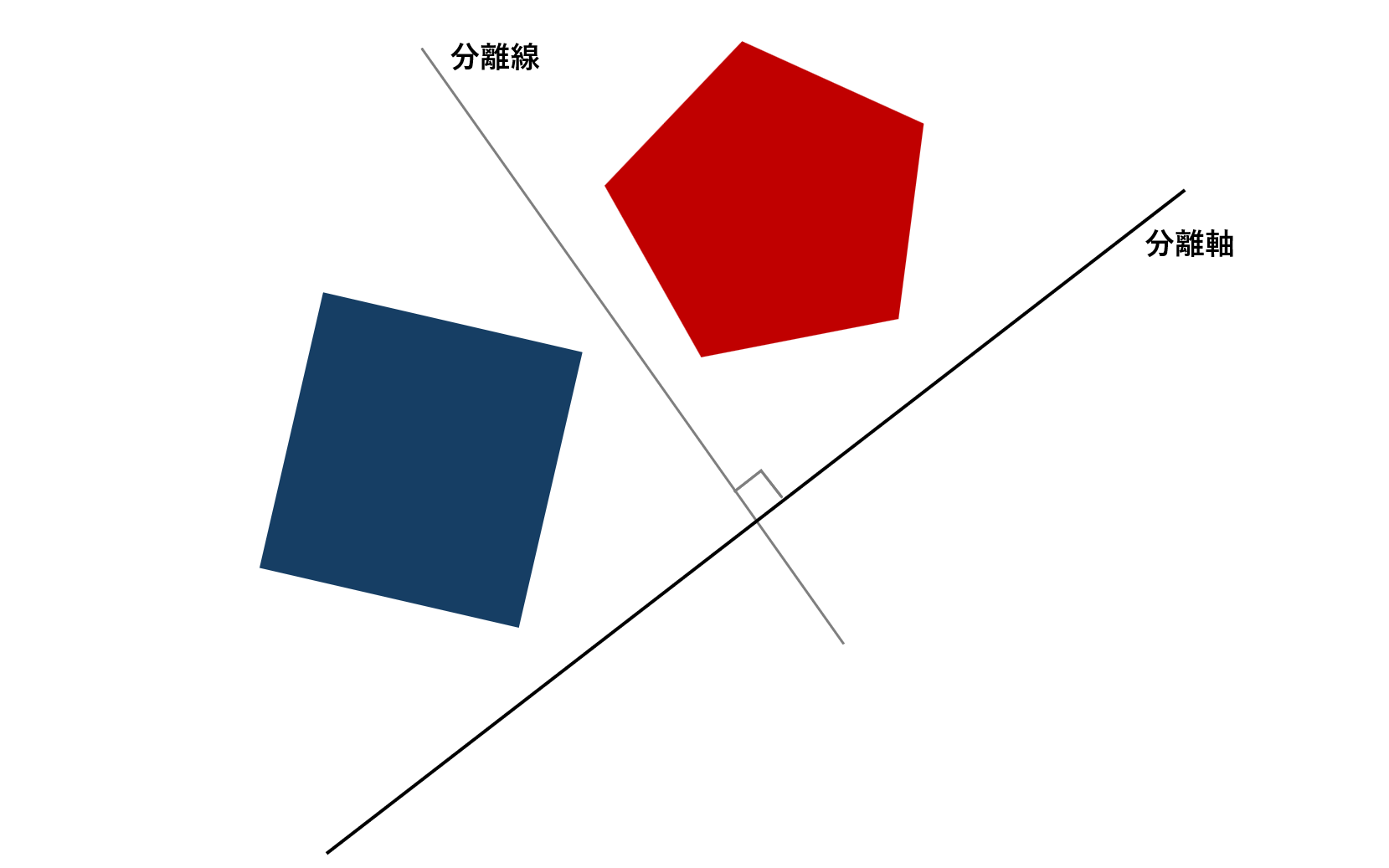
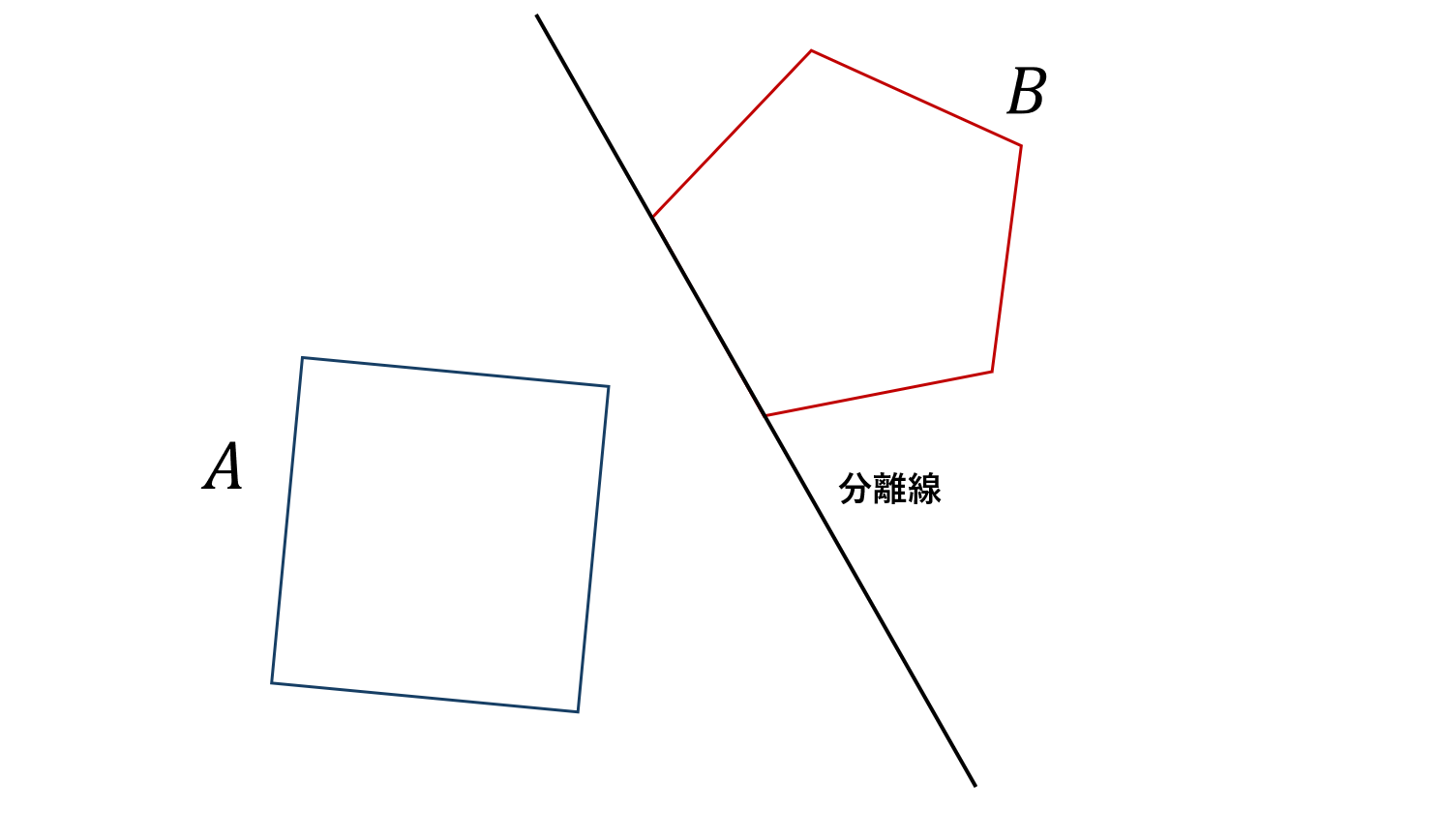
分離超平面定理

「凸な図形同士が重なっていない」とは,

• 直線を用いてこれらを分離できる
• あるアングルから見ると間に隙間ができる

と言い換えることができます. (これは凸じゃないと成り立たないことが容易に理解できると思います.)

「直線を用いてこれらを分離できる」という観点における, 図形を分離する直線を「分離線」と呼ぶことにします.

「あるアングルから見ると間に隙間ができる」という観点における, 「あるアングル」に立って図形を見ている人は, 肩のラインが分離線に垂直になっていることが分かります. この分離線に垂直な線を「分離軸」と呼ぶことにします.

この分離軸の上にスクリーンを置いて, 2つの図形の影を落とすと, これらの影は重ならないことが分かります. つまり, 次のようなことが直感的に理解できます.

$A$と$B$が重ならないならば, 図形の外部に直線 $v$ が存在し, $v$への射影は重ならない.

ところで, いま比喩的に「スクリーンに影を落とす」と書きましたが, スクリーンが図形を貫通するような状況でも問題ありません. 分離軸を平行移動して, 図形を貫通するような位置まで移動させたとします. そのような分離軸に対し, $A$ と $B$ の内部のすべての点を分離軸に対してまっすぐ射影しても, それらの射影は重ならないことが容易に理解できると思います.

要するに分離軸の位置はどうでもよく, 方向だけが重要なのです. 分離軸とは切片と傾きを持った直線ではなく, 傾きのみを持った直線, 方向ベクトルであると再定義しましょう.

$A$と$B$が重ならないならば, あるベクトル $v$ が存在し, $v$ への射影は重ならない.

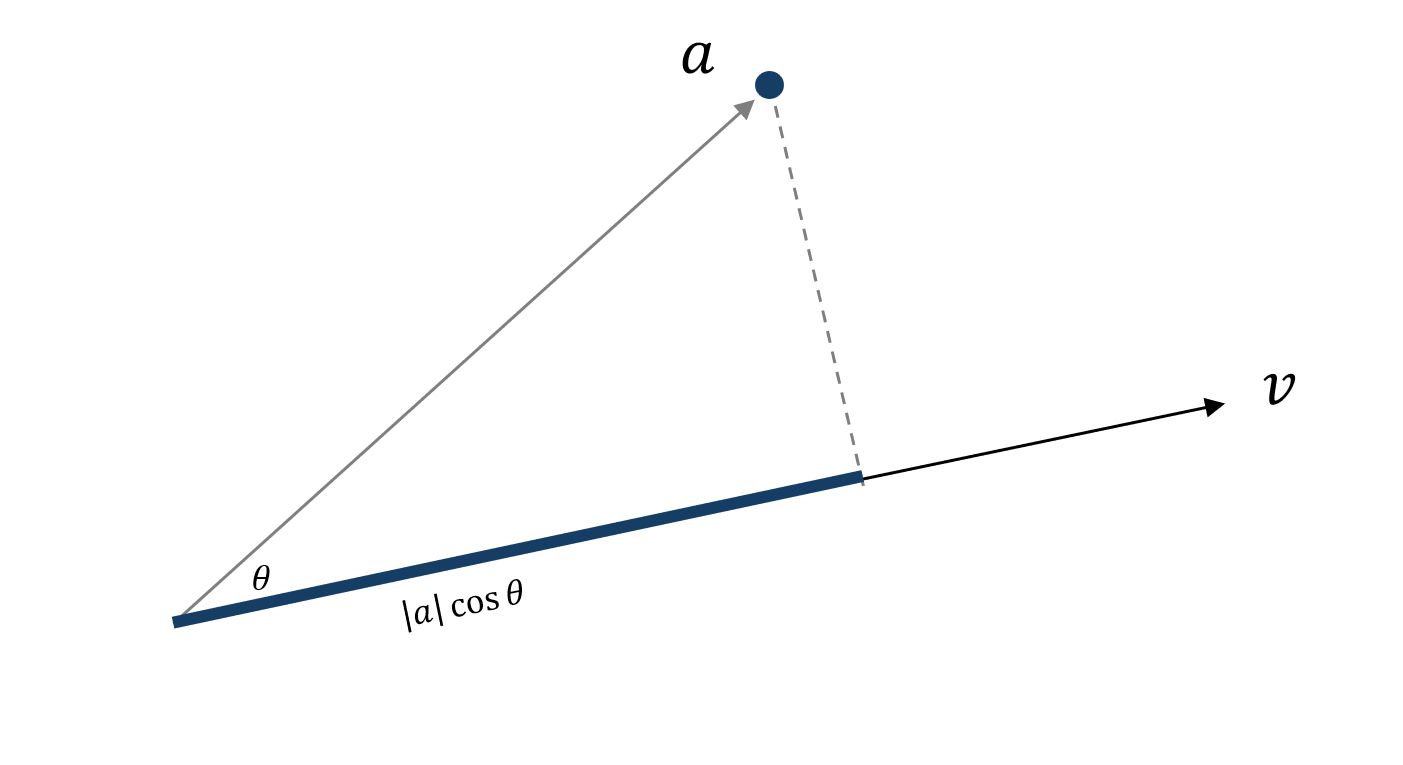
ところで, 射影ってどう計算するのでしょうか? 次の基本的な事実を思い出しましょう.

$a, v$をそれぞれベクトルとする. このとき, 内積 $a\cdot v$は $a$ の $v$ に対する正射影ベクトルの符号付き長さに$v$の長さを掛けたものである.

これは内積というものを幾何的に捉えなおしただけです. 線形代数をやると忘れがちですが, $\mathbb{R}^2$上の内積$a \cdot v$とは幾何的には $|a||v| \cos \theta$ で定義されていたのでした. 内積をとると, 実際に射影されるわけではないですが, 射影したときの長さが分かります. $|v|$倍されますが, $v$を固定すると定数倍なのであまり問題になりません.

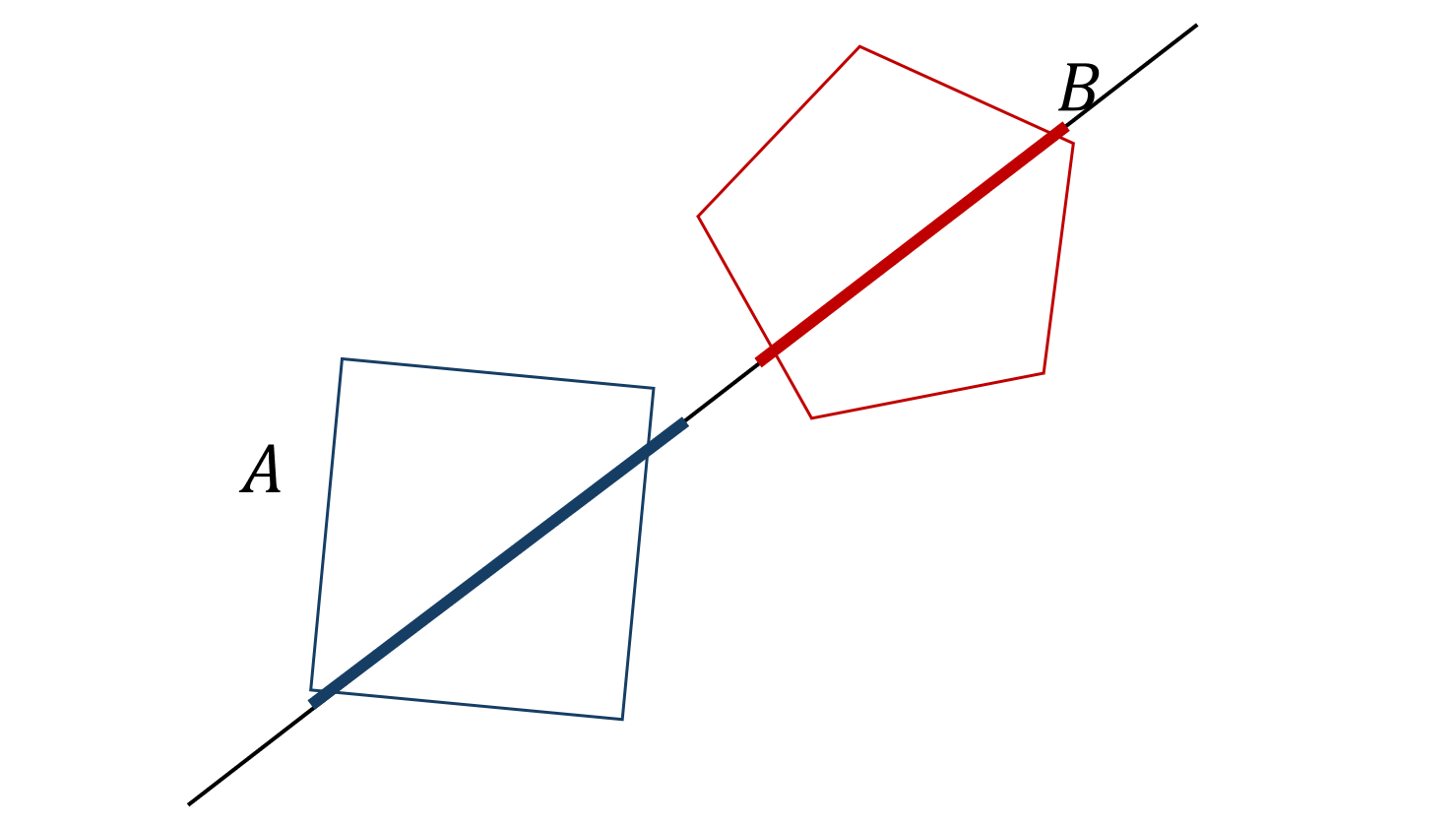
$A$と$B$を分離軸上に射影したとき, それらが重ならないならば, 一次元の場合で見たように分離軸上の点 $c$ によって分離できます. これらの分離軸上の点すべてに正の定数 $|v|$ を掛けても, 位置関係が変化することはありません. 事前に$c$の長さを$|v|$で割っておくと, 次の定理を得ます.

分離超平面定理

$A, B$ は平面上の凸な図形であるとする. このとき, $A$ と $B$ が重ならないならば, 分離軸 $v$ と点 $c$ が存在し, 任意の $a \in A, b\in B$ に対し, $a\cdot v < c$ かつ $c < b\cdot v$.

内積をとると原点からの距離に変換されるので, この$c$とかいう点を計算しなくても一次元の場合のアルゴリズムを呼び出せば判定できます.

1. $A$ と $B$ の各点と分離軸との内積をとる.
2. それらによって定まる閉区間をis_intersect_1d()に代入して判定する.

ところで, 分離軸はどうやって計算するのでしょうか? また, 図形の内部の点をすべて射影するのは現実的でしょうか?

多角形の場合

$A$と$B$が凸多角形で重なっていないとき, 必ずどちらかの辺が分離線として機能するということが分かります.

分離軸とは分離線に垂直なベクトルでした. つまり分離軸の候補は高々 $n+m$ しかありません. あるベクトルに垂直なベクトルを法線ベクトルといい, $(x, y)$を$(-y, x)$に変換することで簡単に計算できます.

さらに, 射影したときに端点になりうる点は図形の頂点のみです. よって, 最初の問題の答えは次のようになります.

1. $n+m$本のすべての辺の法線を計算し, 分離軸の候補とする.
2. すべての分離軸の候補に対し, $A$と$B$の各頂点との内積を計算する.
3. それらの最大値と最小値から閉区間を計算しis_intersect_1d()に代入して判定する.
4. すべての分離軸の候補で射影が重なっていれば$A$と$B$は重なっている. ある分離軸で射影が重なっていないならば$A$と$B$は重なっていない.

def is_intersect_1d(A, B):
    return A[0] <= B[1] and B[0] <= A[1]

# 点列から辺を取得.
# 巡回的に線を引けば元の図形が得られるように定義されているとする.
def edges(A):
    E = []
    n = len(A)
    for i in range(n):
        E.append([A[i][0] - A[(i+1)%n][0], A[i][1] - A[(i+1)%n][1]])
    return E

# 内積
def dot(a, b):
    return a[0]*b[0] + a[1]*b[1]

# 法線
def normal(a):
    return [-a[1], a[0]]

def is_intersect_2d(A, B):
    # すべての辺に対し,
    for e in edges(A)+edges(B):
        # 法線を計算して分離軸の候補とせよ.
        ne = normal(e)
        # AとBの各点を分離軸に射影し,
        pA, pB = [], []
        for a in A:
            pA.append(dot(a, ne))
        for b in B:
            pB.append(dot(b, ne))
        # 一次元に帰着して重なりを判定せよ.
        if not is_intersect_1d([min(pA), max(pA)], [min(pB), max(pB)]):
            # 一つでも分離軸が見つかればAとBは重なっていない.
            return False
    # 分離軸が見つからなければAとBは重なっている.
    return True

if __name__ == "__main__":
    A = [
        [1, 1],
        [1, 2],
        [2, 1]
    ]
    B = [
        [2, 2],
        [2, 3],
        [3, 3],
        [3, 2]
    ]
    print(is_intersect_2d(A, B)) # False
    A = [
        [1, 1],
        [1, 3],
        [3, 3],
        [3, 1]
    ]
    B = [
        [2, 2],
        [2, 4],
        [4, 4],
        [4, 2]
    ]
    print(is_intersect_2d(A, B)) # True
    A = [
        [1, 1],
        [1, 4],
        [4, 4],
        [4, 1]
    ]
    B = [
        [2, 2],
        [2, 3],
        [3, 3],
        [3, 2]
    ]
    print(is_intersect_2d(A, B)) # True

一つ下の次元に帰着させるという構造からわかるように, 同じことを再帰的に行うことで一般の次元に拡張できます.

「超平面」って何?

超平面とは「一つ下の次元の空間」という意味です. 豆腐を切ると断面に平面が得られます. (平面が得られるから断「面」と言っているわけですが.) 三次元の豆腐は中に二次元を持っています. とても当たり前のことを言っています. この断面を超平面と言います.

空間とは本来, 絶対的なものです. 二次元空間を想像するとき, その空間が「どこに」あるのか考えることは普通しません. しかし超平面は違います. 一つ上の次元に所在する相対的なものです. 一つ上の次元から定義される空間なので, 「超」平面といいます. 名前こそ強そうですが, 豆腐を切って得られる程度の概念です.

超「平面」と言っていますが, 平面である必要はありません $n$次元の空間において, その中の$n-1$次元の「まっすぐな」空間はすべて超平面です. 数直線上のすべての点は超平面だし, 平面上のすべての直線もまた超平面です.