GCIデータサイエンティスト育成講座の演習問題を解く Chapter3

GCIデータサイエンティスト育成講座

「GCIデータサイエンティスト育成講座」は、東京大学(松尾研究室)が開講している"実践型のデータサイエンティスト育成講座およびDeep Learning講座"で、演習パートのコンテンツがJupyterNoteBook形式で公開(CC-BY-NC-ND)されています。
Chapter3は「記述統計学と単回帰分析」で、csvファイルの読み込みと基礎的な統計処理、単回帰分析、可視化を学習していきます。
日本語で学べる貴重で素晴らしい教材を公開いただいていることへの「いいね！」ボタンの代わりに、解いてみた解答を載せてみます。間違っているところがあったらご指摘ください。

Chapter3 記述統計学と単回帰分析

3.1.1

[やってみよう]

読み込んだデータを使って、いろいろな視点でデータ集計して、データと対話してみましょう。どんな仮説を考えますか。また、その仮説を確かめるために、どのような実装をしますか。

student_data_math.groupby("G1")["G2"].mean()

> G1
> 3      5.000000
> ...
> 18    18.000000
> 19    18.333333
> Name: G2, dtype: float64

　

[やってみよう]

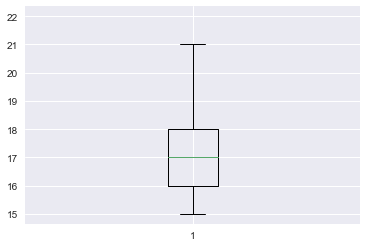
他の変数についても、箱ひげ図を表示させてみましょう。どんな図になっているでしょうか。そこから何かわかることがないか考察してみましょう。

plt.boxplot(student_data_math.age)
plt.grid(True)

　

<練習問題 1>

studet-por.csvを読み込んで、要約統計量を表示してください。

student_data_por = pd.read_csv("student-por.csv", sep=";")
#student_data_por.head()
student_data_por.describe()

省略
　

<練習問題 2>

以下の変数をキーとして、先ほどの数学のデータとポルトガル語のデータをマージしてください。マージするときは、両方ともに含まれているデータを対象としてください（内部結合と言います）。そして、要約統計量など計算してください。なお、以下以外の変数名は、重複がありますので、suffixes=('_math', '_por')のパラメータを追加して、どちらからのデータかわかるようにしてください。

["school","sex","age","address","famsize","Pstatus","Medu","Fedu","Mjob","Fjob","reason","nursery","internet"]

student_data_merge = pd.merge(student_data_math, student_data_por, on=["school","sex","age","address","famsize","Pstatus","Medu","Fedu","Mjob","Fjob","reason","nursery","internet"], suffixes=["_math", "_por"])
student_data_merge.head()

省略
　

<練習問題 3>

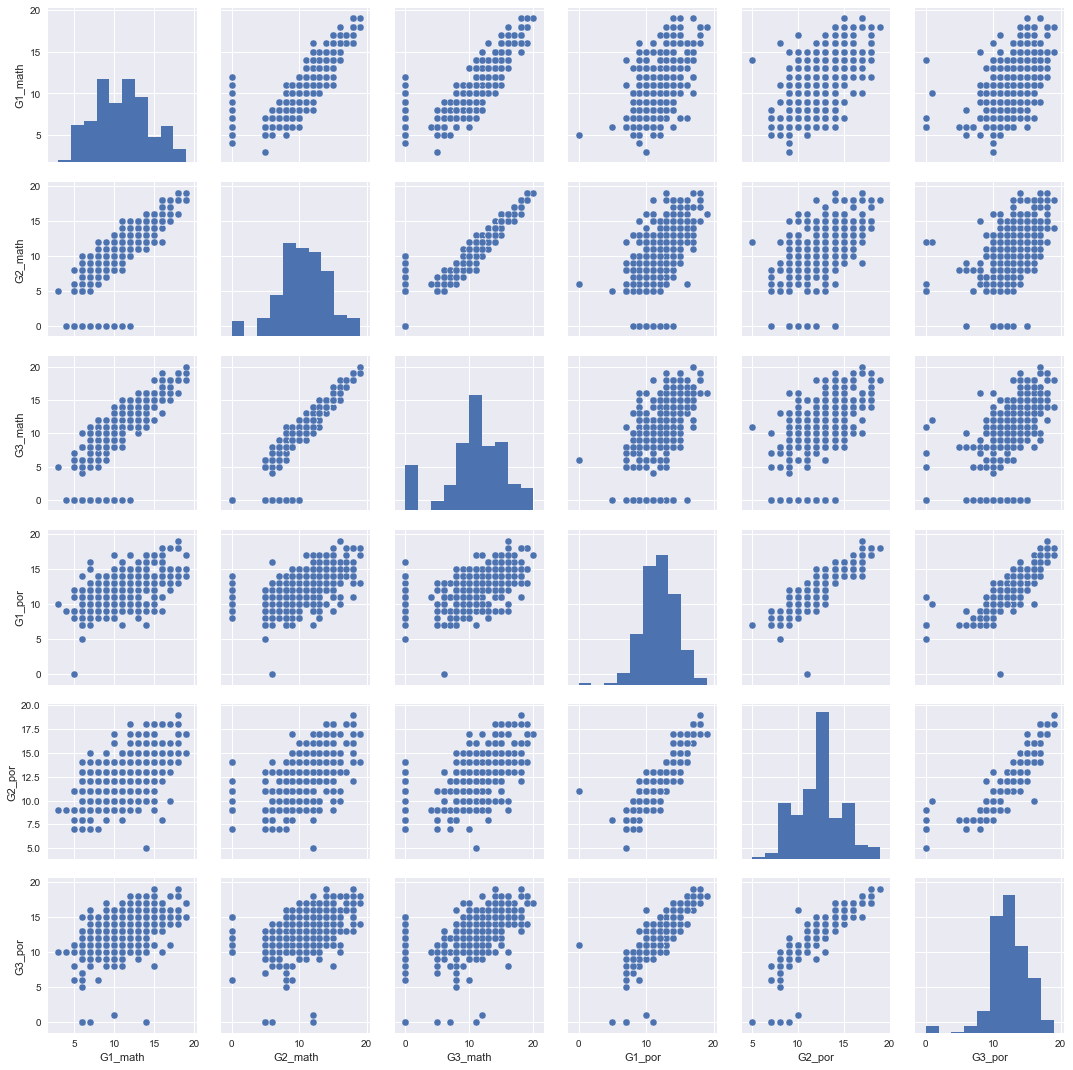
上記のマージしたデータについて、変数を幾つかピックアップして、散布図とヒストグラムを作成してみましょう。どういった傾向がありますか。また、数学データのみの結果と違いはありますか。考察してみましょう。

sns.pairplot(student_data_merge[["G1_math","G2_math","G3_math","G1_por","G2_por","G3_por"]])

　

3.1.2

<練習問題 1>

student-por.csvのデータを使って、G3を目的変数、G1を説明変数として単回帰分析を実施し、回帰係数、切片、決定係数を求めてください。

from sklearn import linear_model

# 線形回帰のインスタンスを生成
clf = linear_model.LinearRegression()

# 説明変数に "一期目の数学の成績" を利用
# ilocはデータフレームから、行と列を指定して取り出す。loc[:, ['G1']]は、G1列のすべての列を取り出すことをしている
# marixの型に直しているので、注意
X = student_data_por.loc[:, ['G1']].as_matrix()

# 目的変数に "最終の数学の成績" を利用
Y = student_data_por['G3'].as_matrix()

# 予測モデルを計算、ここでa,bを算出
clf.fit(X, Y)

# 回帰係数
print("回帰係数:", clf.coef_)

# 切片 
print("切片:", clf.intercept_)

# 決定係数、寄与率とも呼ばれる
print("決定係数:", clf.score(X, Y))

> 回帰係数: [ 0.973]
> 切片: 0.820398412106
> 決定係数: 0.682915680017

　

<練習問題 2>

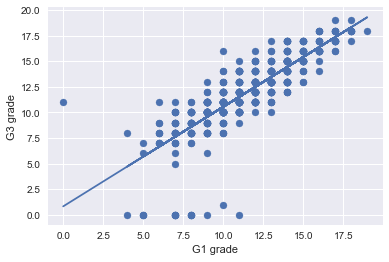
上のデータの実際の散布図と、回帰直線を合わせてグラフ化してください。

# 先ほどと同じ散布図
plt.scatter(X, Y)
plt.xlabel("G1 grade")
plt.ylabel("G3 grade")

# その上に線形回帰直線を引く
plt.plot(X, clf.predict(X))
plt.grid(True)

　

<練習問題 3>

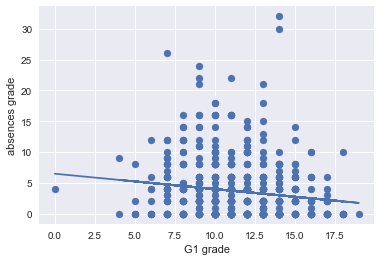
student-por.csvのデータを使って、G3を目的変数、absences(欠席数)を説明変数として単回帰分析を実施し、回帰係数、切片、決定係数を求めてください。この結果を見て、考察してみましょう。

from sklearn import linear_model

# 線形回帰のインスタンスを生成
clf = linear_model.LinearRegression()

# 説明変数に "一期目の数学の成績" を利用
# ilocはデータフレームから、行と列を指定して取り出す。loc[:, ['G1']]は、G1列のすべての列を取り出すことをしている
# marixの型に直しているので、注意
X = student_data_por.loc[:, ['G1']].as_matrix()

# 目的変数に "最終の数学の成績" を利用
Y = student_data_por['absences'].as_matrix()

# 予測モデルを計算、ここでa,bを算出
clf.fit(X, Y)

# 回帰係数
print("回帰係数:", clf.coef_)

# 切片 
print("切片:", clf.intercept_)

# 決定係数、寄与率とも呼ばれる
print("決定係数:", clf.score(X, Y))

# 先ほどと同じ散布図
plt.scatter(X, Y)
plt.xlabel("G1 grade")
plt.ylabel("absences grade")

# その上に線形回帰直線を引く
plt.plot(X, clf.predict(X))
plt.grid(True)

> 回帰係数: [-0.249]
> 切片: 6.49499381918
> 決定係数: 0.0216528993517

　

3.2 総合問題

3.2.1 統計の基礎と可視化

以下のサイトにあるデータ（ワインの品質）を読み込み、以下の問いに答えてください。

http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv

（1）基本統計量（平均、最大値、最小値、標準偏差など）を算出してください。

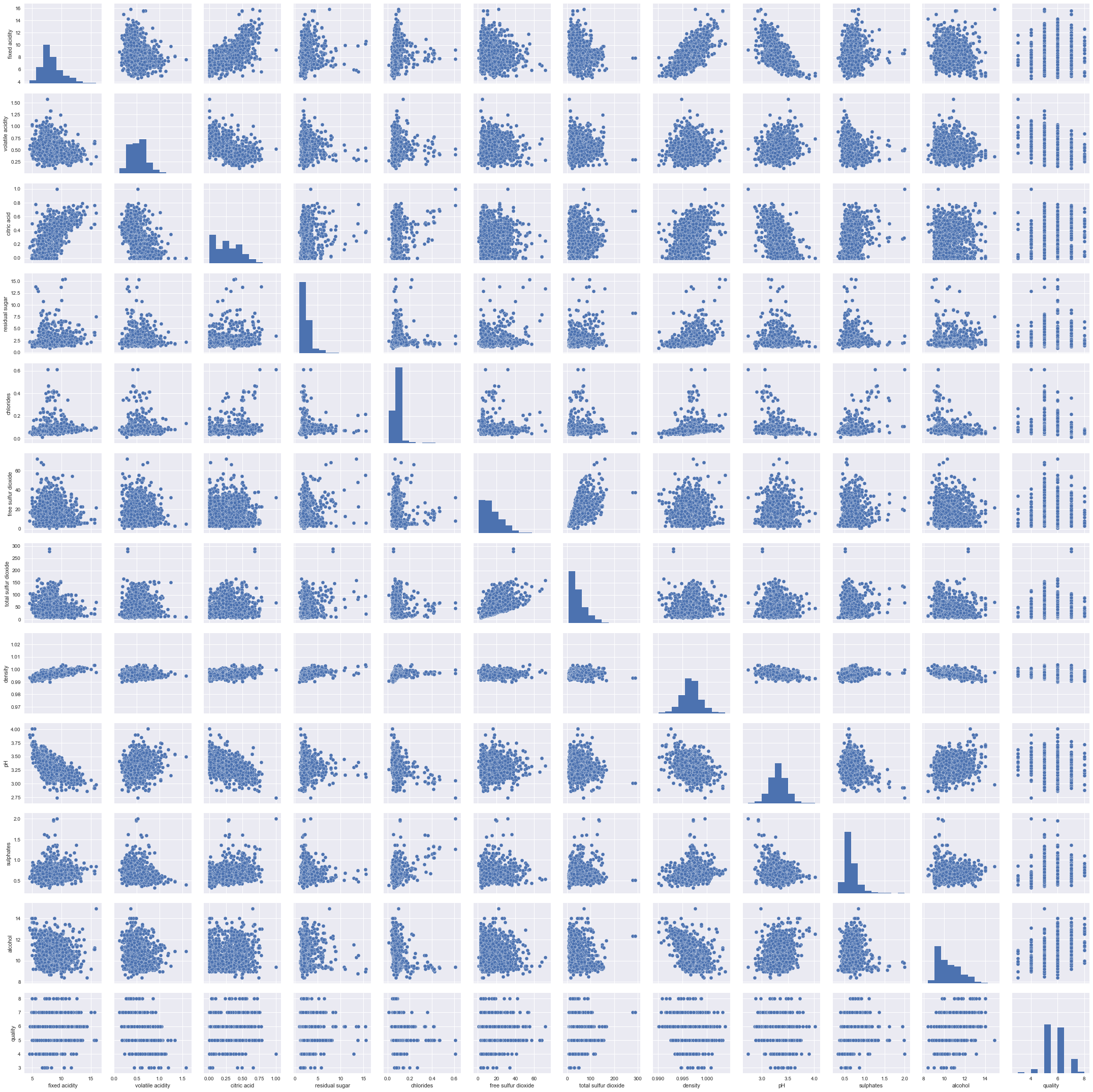
（2）それぞれの変数の分布と、それぞれの変数の関係性（2変数間のみ）がわかるように、グラフ化してみましょう。何かわかる傾向はありますか。

winequality_red_data = pd.read_csv("winequality-red.csv", sep = ";")
#winequality_red_data.head()

print(winequality_red_data.describe())

sns.pairplot(winequality_red_data[["fixed acidity","volatile acidity","citric acid","residual sugar","chlorides","free sulfur dioxide","total sulfur dioxide","density","pH","sulphates","alcohol","quality"]])

省略

　

3.2.2 ローレンツ曲線とジニ係数

3.1の記述統計で使用したstudent_data_mathのデータを使って、以下の問いに答えてください。ここで扱うローレンツ曲線やジニ係数は、貧富の格差（地域別、国別など）を見るための指標として使われています。（なお、本問題は少し難易度が高いため、参考程度に見てください。詳細は、以前に紹介した統計学入門などの文献を参照するか、ネットで検索してください。）

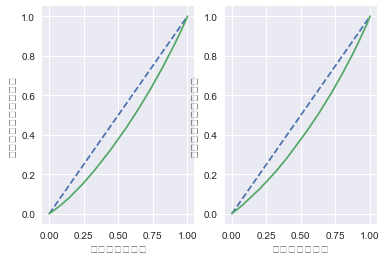
（1）一期目の数学データについて、男女別に昇順に並び替えをしてください。そして、横軸に人数の累積比率、縦軸に一期目の値の累積比率をとってください。この曲線をローレンツ曲線といいます。このローレンツ曲線を男女別に一期目の数学成績でグラフ化してください。

（2）不平等の程度を数値で表したものをジニ係数といいます。この値は、ローレンツ曲線と45度線で囲まれた部分の面積の2倍で定義されて、0から1の値を取ります。値が大きければ大きいほど、不平等の度合いが大きくなります。なお以下のようにジニ係数は定義できます。

\overline{x}は平均値です。

\begin{eqnarray}
GI=\sum_{i}\sum_{j}\left| \frac{x_i-x_j}{2n^2 \overline{x}}\right|
\end{eqnarray}

これを利用して、男女の一期目の成績について、ジニ係数をそれぞれ求めてください。

# (1)
studentM_data_math = student_data_math[student_data_math.sex == "M"]
studentF_data_math = student_data_math[student_data_math.sex == "F"]

mathG1ListM = []
mathG1TotalM = 0.
mathG1ListF = []
mathG1TotalF = 0.
xListM = [i / (len(studentM_data_math) - 1) for i in range(len(studentM_data_math))]
xListF = [i / (len(studentF_data_math) - 1) for i in range(len(studentF_data_math))]

for index, row in studentM_data_math.sort_values("G1").iterrows():
    mathG1TotalM += row["G1"]
    mathG1ListM.append(mathG1TotalM)

for index, row in studentF_data_math.sort_values("G1").iterrows():
    mathG1TotalF += row["G1"]
    mathG1ListF.append(mathG1TotalF)

for i in range(len(mathG1ListM)):
    mathG1ListM[i] = mathG1ListM[i] / mathG1TotalM
for i in range(len(mathG1ListF)):
    mathG1ListF[i] = mathG1ListF[i] / mathG1TotalF

plt.subplot(1,2,1)
plt.plot([0,1], [0,1], linestyle='dashed')
plt.plot(xListM, mathG1ListM)
plt.xlabel("人数の累積比率")
plt.ylabel("一期目の値の累積比率")

plt.subplot(1,2,2)
plt.plot([0,1], [0,1], linestyle='dashed')
plt.plot(xListF, mathG1ListF)
plt.xlabel("人数の累積比率")
plt.ylabel("一期目の値の累積比率")

　

# (2)
# 与式が理解できなかったので普通に計算

giniM = 0.
giniF = 0.

for i in range(len(xListM) - 1):
    giniM += ((xListM[i+1] + xListM[i]) - (mathG1ListM[i+1] + mathG1ListM[i])) * (xListM[i+1] - xListM[i])

for i in range(len(xListF) - 1):
    giniF += ((xListF[i+1] + xListF[i]) - (mathG1ListF[i+1] + mathG1ListF[i])) * (xListF[i+1] - xListF[i])

print(giniM)
print(giniF)

> 0.16752944188428057
> 0.16838887030002433