LiSSAによるInfluence Functionの実装

はじめに

ICML2017のベストペーパーであるUnderstanding Black-box Predictions via Influence Functionsの解説とTensorFlowによる実装です。
提案手法を用いることで、データセットからある学習データを取り除いて学習させた場合のパラメータや損失の変化を推定することができます。
日本語による他の解説記事との主な違いは次の２点です

• LiSSA* (Linear time Stochastic Second-Order Algorithm) によってヘッセ行列の逆行列を近似 (元論文の実装)
• TensorFlowによる実装

*LiSSAについては後述します

手法

前提

学習済みパラメータ$\hat{\theta}$が学習データ$z_1, z_2,...,z_n\left(z_i=\left(x_i,y_i\right)\right)$を用いた以下の最小化問題の解として得られているものとします。
$$
\hat{\theta}\triangleq{argmin}_{\theta}\frac{1}{n}\sum_{i=1}^n L(z_i,\theta)
$$
ここで、経験損失$
\frac{1}{n}\sum_{i=1}^n L(z_i,\theta)$は二階微分可能で凸関数であることを仮定します。

学習データを取り除いた時の損失変化

詳しい導出は省略しますが、学習データ$z$をデータセットから取り除いた時のテストデータ$z_{test}$の損失$L$の変化量$\delta L(z,z_{test})$は上記の仮定のもとで以下のように求めることができます。
$$
\delta L(z,z_{test})\approx-\frac{1}{n}\nabla_{\theta}L(z_{test},\hat{\theta})^{\mathrm{T}} H_{\hat{\theta}}^{-1} \nabla_{\theta}L(z,\hat{\theta})
$$
ここで、$H_{\hat{\theta}}^{-1}$は下式の逆行列で与えられます。
$$
H_{\hat{\theta}}\triangleq \frac{1}{n}\sum_{i=0}^n\nabla_{\theta}^2L(z_i,\hat{\theta})
$$
$z_i$は各学習データ点です。
$H_{\hat{\theta}}^{-1}$は対称行列であることから、次のように$\nabla_{\theta}L(z_{test},\hat{\theta})$と$\nabla_{\theta}L(z,\hat{\theta})$を入れ替えておきます。
$$
\delta L(z,z_{test})\approx-\frac{1}{n}\nabla_{\theta}L(z,\hat{\theta})^{\mathrm{T}} H_{\hat{\theta}}^{-1} \nabla_{\theta}L(z_{test},\hat{\theta})
$$
上式のうち、$H_{\hat{\theta}}^{-1}$の計算コストが非常に大きいため、LiSSAと呼ばれる手法を用いて$s_{test}\triangleq H_{\hat{\theta}}^{-1} \nabla_{\theta}L(z_{test},\hat{\theta})$をまとめて近似することを考えます。

LiSSA (Linear time Stochastic Second-Order Algorithm)

LiSSAはニュートン法の効率的な計算方法に関するものですが、「損失$L$のパラメータ$\hat{\theta}$に関するヘッセ行列の逆行列$H_{\hat{\theta}}^{-1}$」と「任意のベクトル$v\in R^m$ 」の内積をまとめて計算する点が上記計算と共通しています。($m$はパラメータ$\theta$の次元数)

まず、逆行列を元の行列であらわすことを考えます。
${det}A\le1$ となる正定値行列（固有値が全て正である行列）$A$の逆行列$A^{-1}$はテイラー展開によって次のように与えられることが知られています。
$$
A^{-1} = \sum_{i=0}^\infty(I-A)^i
$$
このとき$j$項目までの近似値$A_j^{-1}$は漸化式的に次のように計算できます。
$$
A_j^{-1}\triangleq I+(I-A)A_{j-1}^{-1}
$$
$A=H_{\hat{\theta}}$とすると、上式の両辺にベクトル$v$をかけ、(簡単のため以下$\hat{\theta}$を省略)
$$
H_j^{-1}v=v+(I-H)H_{j-1}^{-1}v = v+H_{j-1}^{-1}v -HH_{j-1}^{-1}v
$$
を得ます。この結果を用いてLiSSAでは以下のように$H^{-1}v$を計算します。

1. $j\gets 0$
2. $H_0^{-1}v \gets v$
3. データセットから学習データ点$z_{sj}$をサンプリング
4. $H_j^{-1}v\gets v+H_{j-1}^{-1}v-\tilde{H}H_{j-1}^{-1}v$
5. $j\gets j+1$
6. 3~5を$j=t$となるまで繰り返す
7. $s_{test}\gets H_t^{-1}v$

ただし2.で計算量削減のため、$H$のかわりに不偏推定量である$\tilde{H}\triangleq\nabla_{\theta}^2L(z_{sj},\hat{\theta})$を用います。
また、結果を安定させるため1~7を複数回実行し、得られた$s_{test}$の平均値を最終的な出力とします。

HVP (Hessian Vector Product)

ニューラルネットの場合、上記2.で必要になる$\tilde{H}=\nabla_{\theta}^2L(z_{sj},\hat{\theta})$の計算コストは依然として高いため、$\tilde{H}H_{j-1}^{-1}v$をまとめて計算することを考えます。ヘッセ行列に任意のベクトルを掛けたものは**HVP (Hessian Vector Product)**と呼ばれ、[効率的な計算方法が提案されています]
(http://www.bcl.hamilton.ie/~barak/papers/nc-hessian.pdf)。

簡単には、ヘッセ行列$H$と任意のベクトル$u\in R^m$の内積に対し次のような式変形を行います。
$$
\begin{eqnarray}
Hu&=&\nabla_{\theta}^2Lu\
&=&\nabla_{\theta}\left(\nabla_{\theta}Lu\right)\
\end{eqnarray}
$$
スカラ値となるカッコ内を先に計算することで、巨大なヘッセ行列を計算することなく、正確なHVPを得ることができます。LiSSAの計算時には$L=L(z_{sj},\hat{\theta})$、$u=H_{j-1}^{-1}v$を代入すればOKです。

スケーリング

LiSSAのテイラー展開で行列$A$が${det}A\le1$を満たすことを仮定しましたが、実際の$H$や$\tilde{H}$が${det}H\le1$を満たす保証はなく、その場合計算の過程で$H_j^{-1}v$が発散してしまいます。そこで$H$を定数$\frac{1}{a}$によってスケーリングすることでこれを回避します。スケーリングした$\frac{1}{a}H$を用いて$H^{-1}$は次のようにあらわすことができます。
$$
H^{-1}=\frac{1}{a} \left( \frac{1}{a}H\right)^{-1}
$$
両辺に$\left( \frac{1}{a}H\right)$をかければ正しいことが確認できると思います。
この結果によれば、LiSSAの計算では下式を扱えばよいことになります。
$$H_j^{-1}v = \frac{1}{a}\sum_{i=0}^j\left(I-\frac{1}{a}H\right)^i v$$

実装

以上を踏まえたtensorflowによる実装です。
https://github.com/nayopu/influence_function_with_lissa
著者による実装から少しシンプルに実装を変更しています。(著者の実装)

以下、LiSSAの関数を抜粋します。

def get_inverse_hvp_lissa(self, v, x, y, scale=10, num_samples=5, recursion_depth=1000, print_iter=100):

    inverse_hvp = None

    for i in range(num_samples):
        print('Sample iteration [{}/{}]'.format(i+1, num_samples))
        cur_estimate = v
        permuted_indice = np.random.permutation(range(len(x)))

        for j in range(recursion_depth):
            x_sample = x[permuted_indice[j]:permuted_indice[j]+1]
            y_sample = y[permuted_indice[j]:permuted_indice[j]+1]

            # get hessian vector product
            hvp = self.sess.run(self.hvp, feed_dict={self.x: x_sample,
                                                     self.y: y_sample,
                                                     self.u: cur_estimate})

            # update hv
            cur_estimate = v + cur_estimate - hvp / scale

            if (j % print_iter == 0) or (j == recursion_depth - 1):
                print("Recursion at depth {}: norm is {}".format(j, np.linalg.norm(cur_estimate)))

        if inverse_hvp is None:
            inverse_hvp = cur_estimate / scale
        else:
            inverse_hvp = inverse_hvp + cur_estimate / scale

    inverse_hvp = inverse_hvp / num_samples
    return inverse_hvp

結果

MNISTの1と7を分類するロジスティック回帰を対象にします。
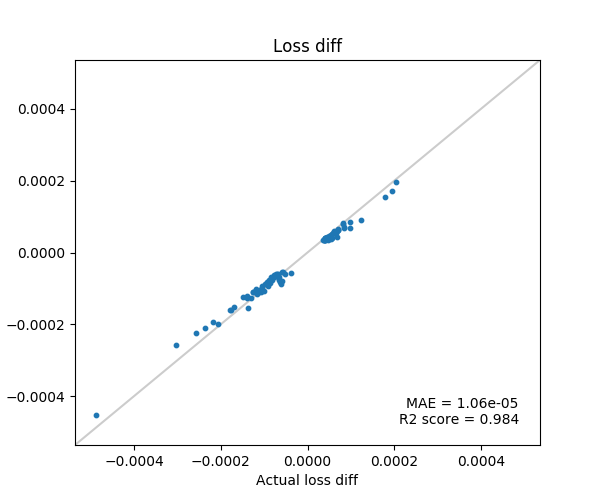
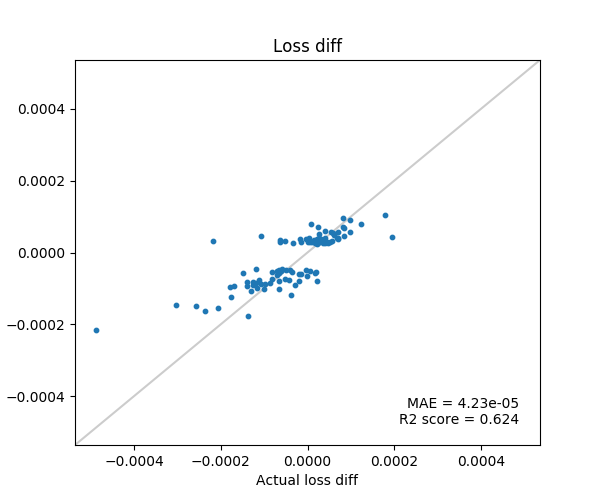
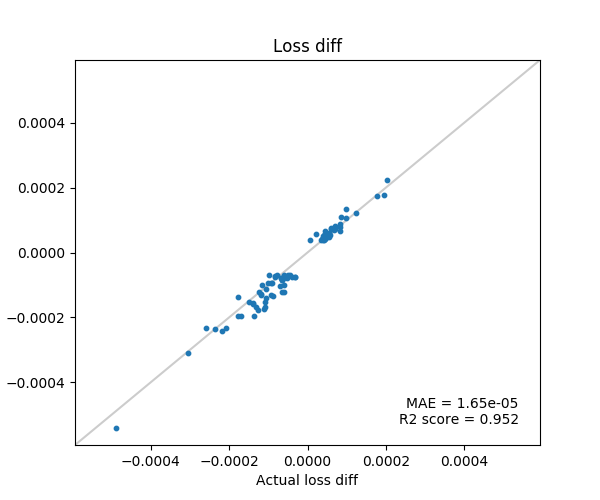
以下、Influence Functionで推定した損失の変化を縦軸、実際に学習データを1つ除外して再学習した場合の損失の変化を横軸にプロットしています。
推定した損失変化値が上位50個と下位50個のデータのみ実験に使用。

• テイラー展開の項数: 1000

• $s_{test}$のサンプル回数: 5
  

• テイラー展開の項数: 100

• $s_{test}$のサンプル回数: 5
  

• テイラー展開の項数: 1000

• $s_{test}$のサンプル回数: 1
  

論文にもある通り、$s_{test}$のサンプル数は1でもよい結果がでますが、テイラー展開はかなり高次の項まで計算しないと精度が出ないようです。
以上。