元論文
Understanding Black-box Predictions via Influence Functions
ICML2017のベストペーパーです。
概要
非常に内容の濃い論文ですが、主なコントリビューションは以下の3点にまとめられると思います。
- 影響関数(influence function)を用いて、個々の学習データの有無や摂動が予測結果に与える影響を定式化
- 効率的な計算手法の提案
- 「ネットワーク挙動の分析」、「ネットワークを混乱させる摂動の計算」、「ドメイン不適合の検知」、「ノイズラベルの検出」の4つのユースケースの紹介
手法
準備
学習データを$z_1$, $z_2$,..., $z_n$($z_i=(x_i,y_i)$)、パラメータ$\theta$のネットワークの損失を$\frac{1}{n}\sum_{i=1}^n L(z_i,\theta)$とします。
定式化にあたって以下の2つを仮定します。
- 損失は二階微分可能
- 損失を最小にする$\hat{\theta}$が既知
後に仮定を緩めた場合の計算方法についても触れます。
学習データの再重み付けによる損失の変化
ある学習データを学習しなかった時、予測結果はどう変わるのでしょう。
すべてのデータを学習したネットワークのパラメータ$\hat{\theta}$、学習データ$z$を学習しなかったネットワークのパラメータ$\hat{\theta}_{-z}$をそれぞれ以下のように定義します。
$$
\begin{eqnarray}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hat{\theta} &\equiv& \argmin_{\theta} \sum_{i=0}^n L(z_i,\theta)\
\hat{\theta}_{-z} &\equiv& \argmin_{\theta} \sum_{z_i \neq z} L(z_i,\theta)
\end{eqnarray}
$$
目的はパラメータ$\hat{\theta}_{-z}$のネットワークを用いてテストデータ$z_{test}$を入力したときの損失を求めることです。現状のパラメータ$\hat{\theta}$で出力される損失と比較することでその学習データ$z$が予測結果に与える影響を調べることができます。
まずパラメータの変化量$\hat{\theta}_{-z}-\hat{\theta}$を求めます。
再学習すれば$\hat{\theta}_{-z}$を求められますが、言うまでもなく計算コストがかかります。そこで影響関数を用いることで効率的に$\hat{\theta}_{-z}$を求められます。
$\hat{\theta}_{-z}$を求めるために、より一般的な
$$
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hat{\theta}_{\epsilon,z} \equiv \argmin_{\theta} \frac{1}{n} \sum_{i=0}^n L(z_i,\theta) + \epsilon L(z,\theta)
$$
を定義します。これは学習データ$z$を$\epsilon$の重みを付けて再学習したときのネットワークのパラメータとみなせます。$\epsilon=-\frac{1}{n}$とすれば$\hat{\theta}_{-z}$と等しくなることがわかります。
$\hat{\theta}_{\epsilon,z}$の$\epsilon=0$での微分係数は先行研究(Cook & Weiberg, 1982)により以下の式で求められます。論文のAppendixにも詳しい計算方法が載っています。
$$
\mathcal{I}_{up,param}(z)\equiv \left. \frac{d\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}=-H_{\hat{\theta}}^{-1} \nabla_{\theta}
L(z,\hat{\theta})
$$
$H_{\hat{\theta}}\equiv \frac{1}{n}\sum_{i=0}^n\nabla_{\theta}^2L(z_i,\hat{\theta})$はヘッシアンで、2つ目の仮定により正定値行列となり、逆行列を計算できることが保証されます。上式を用いると、$\epsilon$が微小量の時、$\hat{\theta}_{\epsilon,z} \approx \hat{\theta} + \mathcal{I}_{up,param}(z)\epsilon$と近似できるため
$$
\hat{\theta}_{-z} -\hat{\theta}=\hat{\theta}_{-\frac{1}{n},z} - \hat{\theta}\approx -\frac{1}{n} \mathcal{I}_{up,param}(z)
$$
と求められます。以上で再学習せずにパラメータの変化量を計算することができました。
パラメータの変化量が求まれば、テストデータ$z_{test}$を入力したときの損失の変化量$\delta L(z,z_{test})$は以下のように求めることができます。
$$
\begin{eqnarray}
\mathcal{I}_{up,loss}(z,z_{test})&\equiv& \left. \frac{dL(z_{test},\hat{\theta}_{\epsilon,z})}{d\epsilon}\right|_{\epsilon=0}\
&=& \nabla_{\theta}L(z_{test},\hat{\theta})^{\mathrm{T}}\left. \frac{d\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}\
&=& -\nabla_{\theta}L(z_{test},\hat{\theta})^{\mathrm{T}} H_{\hat{\theta}}^{-1} \nabla_{\theta}L(z,\hat{\theta})
\end{eqnarray}
$$
$$
\delta L(z,z_{test})\approx-\frac{1}{n}\mathcal{I}_{up,loss}(z,z_{test})
$$
以上で学習データ$z$を学習しなかったときの$z_{test}$の損失の変化量$\delta L(z,z_{test})$を求めることができました。
例えばロジスティック回帰の場合、$\mathcal{I}_{up,loss}(z,z_{test})$は以下のように求めることができます。
$$
\mathcal{I}_{up,loss}(z,z_{test})=-y_{test}\sigma(-y_{test}\theta^{\mathrm{T}}x_{test})y\sigma(-y\theta^{\mathrm{T}}x)x_{test}^{\mathrm{T}}H_{\hat{\theta}}^{-1}x\
H_{\hat{\theta}}=\frac{1}{n}\sum_{i=1}^n\sigma(\theta^{\mathrm{T}}x_i)\sigma(-\theta^{\mathrm{T}}x_i)x_i x_i^{\mathrm{T}}
$$
$y \in \{-1,1\}$、$\sigma(x) = \frac{1}{1+e^{-x}}$です。ロジスティック回帰の事後確率は$p(y|x) = \sigma(y \theta^{\mathrm{T}} x)$で表されますので、$\mathcal{I}_{up,loss}$が$\sigma(-y\theta^{\mathrm{T}}x)$に比例するということは予測が不確な学習データほど損失に大きな影響を及ぼしていることがわかります。
この点が単なるコサイン類似度などと比べて影響関数が優れている理由の一つです。
学習データ摂動による損失の変化
$z=(x,y)$を$z_{\delta}\equiv(x+\delta,y)$として学習したときのパラメータの変化量、損失の変化量も影響関数を用いて計算することができます。
$z$を$z_{\delta}$として学習したときのパラメータ$\hat{\theta}_{\epsilon,z_{\delta},-z}\equiv {\mathop{\rm arg~min}\limits}_{\theta}\frac{1}{n} \sum_{i=0}^nL(z_i,\theta)+\epsilon L(z_{\delta},\theta)-\epsilon L(z,\theta)$の$\epsilon=0$での微分係数は
$$
\begin{eqnarray}
\left. \frac{d\hat{\theta}_{\epsilon,z_{\delta},-z}}{d\epsilon}\right|_{\epsilon=0}&=&\mathcal{I}_{up,param}(z_{\delta})-\mathcal{I}_{up,param}(z)\
&=&-H_{\hat{\theta}}^{-1} (\nabla_{\theta}
L(z_{\delta},\hat{\theta})-\nabla_{\theta}
L(z,\hat{\theta}))
\end{eqnarray}
$$
となります。これは$\delta$が微小量のとき、$\left. \frac{d\hat{\theta}_{\epsilon,z_{\delta},-z}}{d\epsilon}\right|_{\epsilon=0} \approx -H_{\hat{\theta}}^{-1} [\nabla_x \nabla_{\theta}
L(z,\hat{\theta})]\delta$と近似できるので、$z_{test}$を入力としたときの$\delta=0$の周りでの損失の勾配は
$$
\begin{eqnarray}
\mathcal{I}_{pert,loss}(z,z_{test})^{\mathrm{T}} &\equiv& \left. \nabla_{\delta} L(z_{test},\hat{\theta}_{z_{\delta},-z})^{\mathrm{T}} \right|_{\delta=0}\
&=& -\nabla_{\theta}L(z_{test},\hat{\theta})^{\mathrm{T}} H_{\hat{\theta}}^{-1} \nabla_x \nabla_{\theta}L(z,\hat{\theta})
\end{eqnarray}
$$
と計算されます。損失の変化量は$\mathcal{I}_{pert,loss}(z,z_{test})^{\mathrm{T}}\delta$で求めることができ、$\delta$が$\mathcal{I}_{pert,loss}(z,z_{test})$と同じ方向の時、損失の増加量が最大になります。これはAdversarial Trainingなどにおける最もネットワークを混乱させる摂動と似ていますが、ここで求めたのはあるテストデータ$z_{test}$を識別しづらくするために学習データ$z$に加える摂動である点に注意が必要です。
効率的な計算方法
$\mathcal{I}_{up,loss}(z,z_{test})$の計算は以下の2点の理由で計算量が大きくなってしまいます。
- 損失関数のヘッシアンの逆行列$H_{\hat{\theta}}^{-1}$の計算
- 全訓練データに対する$\mathcal{I}_{up,loss}(z,z_{test})$の反復的な計算
そこで、$H_{\hat{\theta}}^{-1}$を直接計算するのではなく$s_{test} \equiv H_{\hat{\theta}}^{-1} \nabla_{\theta}
L (z_{test},\hat{\theta})$を近似を用いて計算することで計算量を削減します。さらに、$s_{test}$を事前に求めておくことで、各学習データ$z$に対しては$\mathcal{I}_{up,loss}(z,z_{test})=-s_{test} \nabla_{\theta}L(z,\hat{\theta})$を計算するだけでよく2点目の計算量増大の要因も解決できます。
詳細な説明は省略しますが以下の手順で$s_{test}$の近似値が求められるようです。
- $v\gets\nabla_{\theta} L (z_{test},\hat{\theta})$
- $\tilde{H}_0^{-1}v \gets v$
- $\tilde{H}_{j}^{-1}v \gets v+(I-\nabla_{\theta}^2 L(z_{sampled},\hat{\theta}))\tilde{H}_{j-1}^{-1}v~~~~~(j=1,2,...,t)$
- $s_{test}\gets\tilde{H}_{t}^{-1}v $
損失関数が収束しない場合の計算方法
実際の問題で$\mathcal{I}_{up,loss}$を求めようとすると、$H_{\hat{\theta}}$の逆行列を求めることができずに躓くことがあると思います。これは最急降下法などで求めたネットワークのパラメータの推定値$\tilde{\theta}$が最適値$\hat{\theta}$に収束していないことが原因です。$\tilde{\theta}$を用いて計算した$H_{\tilde{\theta}}$はもはや正定値ではないため逆行列を求めることができなくなります。
損失が最小となる$\hat{\theta}$を見つけるのはしばしば現実的ではないため、$\hat{\theta}$に近いパラメータ推定値$\tilde{\theta}$を用いて$\mathcal{I}_{up,loss}$を計算する方法が紹介されています。
完全には理解できておらず間違っているかもしれませんが、学習データ$z$間で$\mathcal{I}_{up,loss}$を比較するという用途であれば$H_{\hat{\theta}}^{-1} \to (H_{\hat{\theta}}+\lambda I)^{-1}$とすれば良いようです。$\lambda$は減衰項(damping term)と呼ばれており、元論文の例では$\lambda=0.01$などの値を用いています。
上で、「学習データ$z$間で$\mathcal{I}_{up,loss}$を比較するという用途であれば」と書いたのは$\hat{\theta}$の代わりに$\tilde{\theta}$を用いると$\mathcal{I}_{up,loss}$が$z$に依存しない量だけシフトするためです。この量は$g\equiv \frac{1}{n}\sum_{i=0}^n\nabla_{\theta}L(z_i,\tilde{\theta})$に依存しており$\tilde{\theta}=\hat{\theta}$では$g=0$になります。
手書き数字識別における影響関数の分析
ロジスティック回帰を用いたMNISTの2クラス識別問題を解き、$\mathcal{I}_{up,loss}$を求めてみました。
実装
折角$H_{\hat{\theta}}^{-1}$の効率的な計算方法が紹介されていますが、今回は問題が簡単でパラメータも少ないので直接$H_{\hat{\theta}}^{-1}$を求めています。
MNISTを用いたロジスティック回帰では$H_{\hat{\theta}}=\frac{1}{n}\sum_{i=1}^n\sigma(\theta^{\mathrm{T}}x_i)\sigma(-\theta^{\mathrm{T}}x_i)x_i x_i^{\mathrm{T}}$がランク落ちするので注意が必要です。これは、全ての学習画像のフチ部分が0なので784x784行列である$\sum_{i=1}^n x_i x_i^{\mathrm{T}}$の複数の列ベクトルが0ベクトルになることを考えれば容易にわかります(バイアス項を無視していますが、バイアス項を考慮しても結果は同じです)。実際、何も考えずに$H$を求めるとランクは500程度しかありませんでした。
私は学習画像に僅かなランダムノイズを加えることで解決しました。下図のMNISTの画像もよく見るとランダムノイズが入っています。
実験結果
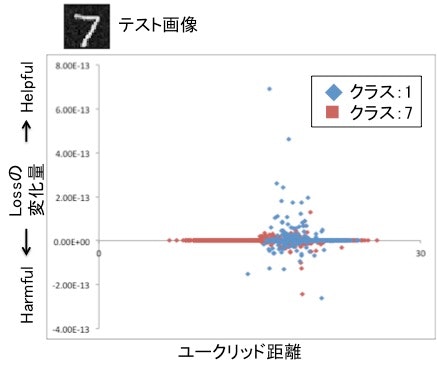
まず、1と7の分類を考えます。
下図はあるテストデータに対して横軸にユークリッド距離、縦軸に損失の変化量($-\frac{1}{n}\mathcal{I}_{up,loss}$)をとり、全訓練データをプロットしたものです。損失の変化量が正のデータほど、そのデータを学習しなかったときにテストデータの損失が大きくなる、すなわち誤識別が起きやすくなるため、そのテストデータの識別に役立っている(helpful)といえます。逆に負のデータほど学習しなかったときに損失が現状より少なくなる、すなわち識別しやすくなるため、識別を阻害している(harmful)といえます。
グラフから読み取れることは2点あります。
-
ユークリッド距離と損失の変化量はほとんど相関がない
これは元論文で述べられているとおり$\mathcal{I}_{up,loss}$はユークリッド距離よりも本質的な表現を抽出する事ができるためと考えられます。 -
学習データのクラスよらずhelpfulなデータとharmfulなデータが存在する。
これについては下記の具体例を用いて考察します。
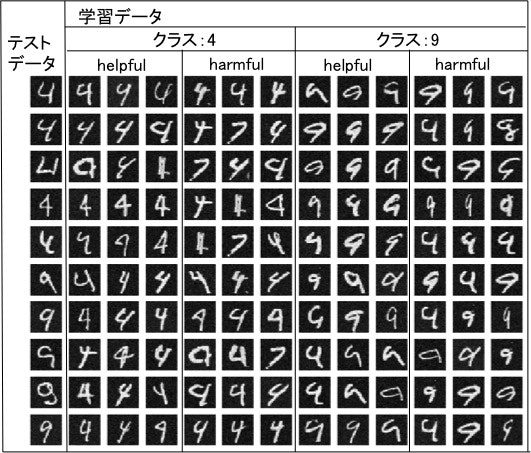
下図は10個のテストデータに対するhelpfulな学習画像とharmfulな学習画像を各クラスごとに上位3個ずつ(左から1位、2位、3位)表示したものです。
テストデータと同じクラスでhelpfulになる画像は、単に似ているだけでなく、$-\frac{1}{n}\mathcal{I}_{up,loss}$が$\sigma(-y\theta^{\mathrm{T}}x)$に比例していることから分かる通り、現状の識別機での不確かさも兼ね揃えているデータが選ばれます。逆に同じクラスでharmfulなデータにテストデータと似てない不確かなデータが選ばれる傾向が見られます。直感的には自分と似てないものまで同じクラスと学習すると、自分の確信度が下がる、と解釈できます。
異なるクラスを見ると、自分と似てるのもがharmful、似てないもので不確かなデータがharmfulになる傾向が見られます。
1と7の例では少し分かりづらいので4と9の例も実験しました。特に5行目の4の結果は上記の説明によく当てはまっているように思えます。
ユースケース
元論文で紹介されている4つのユースケースを簡単に説明します。
ネットワーク挙動の分析
上記の実験の本格的なバージョンです。Inception v3で魚と犬を識別する実験を行っています。

 (元論文より引用)
(元論文より引用)
上図は魚のTest Image(左上)を入力したときのhelpfulな画像2枚(右)と横軸をユークリッド距離、縦軸を$-\frac{1}{n}\mathcal{I}_{up,loss}$として学習データをプロットしたグラフ(左下)を示しています。
ネットワークを混乱させる摂動の計算
$\mathcal{I}_{purt,loss}$を用いて、最も損失を大きくする摂動の方向を計算することができます。
 (元論文より引用)
(元論文より引用)
図左上に示す魚クラスの学習画像(犬に見えますが…)に計算で求めた摂動を加えて再学習すると、図下段に示すような犬クラスのテストデータを魚クラスと誤って識別させることができました。
ドメイン不適合の検知
診断データから再入院の可能性を予測する問題を考えます。
子供の再入院発生率が高くなるように意図的に操作したデータセットを学習した識別器を用いて、テストデータの子供の再入院する確率を予測した時、通常より再入院する確率が大きく予測されてしまいます。影響関数を用いることで、この結果が意図的に操作した子供の学習データに大きく依存するものと特定できました。
すなわち、予測結果に対する依存度の高い学習データの分布を見ることで、ドメイン不適合を発見しやすくすることができると考えられます。
ノイズラベルの検出
学習データに誤ったラベルの付与されたデータが混入している場合、人間によるラベル修正が必要ですが、どのような優先順位でラベルの誤ってそうな怪しいデータをチェックしていくかは工夫が必要です。従来は損失の大きい学習データを怪しいデータとしてピックアップしていましたが、影響関数を用いることでより効果的に候補データをピックアップできたと報告しています。