重心分解は木の分割統治法のひとつで、特にパスクエリに有効とされています。
しかしPythonでの実装例が少なかったので、備忘録として私の実装例を残しておきます。
自分用 行数削減版
自分用の重心分解(行数削減版)です。
パソコンが壊れた時用に置いておきます。(終)
#重心分解
class Centroid_decomposition:
def __init__(self, N: int, G: list[int]):
#order[c]: 重心分解後の部分木における、重心cのDFS到達順
# 重心cの部分木は、orderが重心cよりも「大きい」BFSで移動可能な頂点
#depth[c]: 重心分解後の部分木における、重心cの深さ
#belong[c]: 重心木cより1サイズ大きい重心木の重心(なければ-1)
# belong[c]を再帰的にたどることで、頂点iが属する重心を列挙できる
self.N, self.logN = N, N.bit_length()
self.order, self.depth, self.belong = [-1] * N, [-1] * N, [-1] * N
stack, size = [(0, -1)], [1] * N
for now, back in stack:
for nxt in G[now]:
if nxt != back: stack.append((nxt, now))
while stack: now, back = stack.pop(); size[back] += size[now] if now else 0
stack = [(0, -1, 0)]
for i in range(N):
now, back, d = stack.pop()
while True:
for nxt in G[now]:
if self.order[nxt] == -1 and size[nxt] * 2 > size[now]:
size[now], size[nxt], now = size[now] - size[nxt], size[now], nxt
break
else: break
self.order[now], self.depth[now], self.belong[now] = i, d, back
if size[now] > 1:
for nxt in G[now]:
if self.order[nxt] == -1: stack.append((nxt, now, d + 1))
def find(self, u: int, v: int): #u - c - v の位置関係となる唯一の重心cを探す
du, dv = self.depth[u], self.depth[v]
for du in range(du - 1, dv - 1, -1): u = self.belong[u]
for dv in range(dv - 1, du - 1, -1): v = self.belong[v]
while u != v: u, v = self.belong[u], self.belong[v]
return u
def get(self, v: int): #頂点vが属する重心木を、サイズの昇順に列挙する
vertices = []
for d in range(self.depth[v] + 1): vertices.append(v); v = self.belong[v]
return vertices
重心分解のアルゴリズム
蟻本に準じた、再帰的な分割を行います。
具体的には以下の通りです。
- 適当な頂点を根として、各子の部分木の大きさを求める。
- 重心を探す。
すべての子の部分木の大きさが親の半分以下になるまで、よりサイズが大きい子に移動する。 - 重心の決定順を採番してから、重心を除いた部分木に再帰的に重心分解を行う。
重心分解により、木は$N$個の重心木に部分分解されます。
参考までに、重心分解の例を図に残しておきます。
重心分解の説明 (図10枚)
周囲の部分木の大きさが全体の半分以下になるまで、頂点を移動します。
移動先はより大きい方向を選べばよいです。



重心が見つかったら、重心の決定順を示す値を記録します。(右下の値です)

続いて、重心を除いたグラフに対して再帰的な重心分解を行います。
再帰のはじめ先は頂点2, 4, 7が候補ですが、今回は頂点7から再帰を行います。
頂点7は重心の条件を満たすため、決定順が2番目であることを記録します。

以降、再帰的に分解を繰り返します。



重心分解は、特に木上のパスクエリで威力を発揮します。
重心分解を行うと、任意のパスを「ある重心をかならず通過するパス」として解釈できるようになります。
このように、「根をかならず通るパス」という部分問題に読み替えることができるのが重心分解の強みです。
たとえば以下のような9頂点の木を考えます。
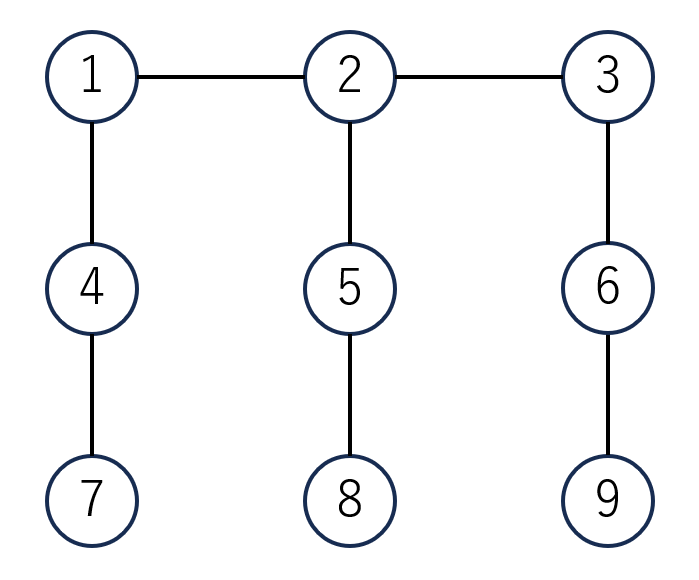
この木を重心分解すると、図のような9個の重心木に分解できます。
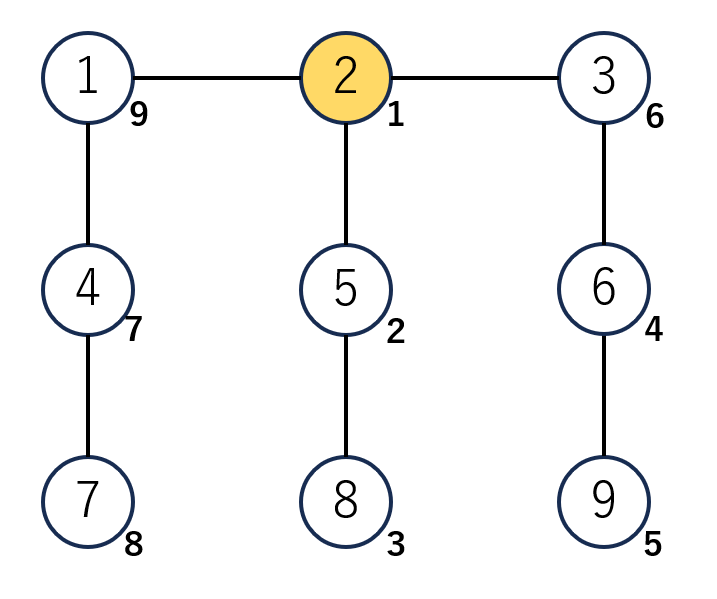
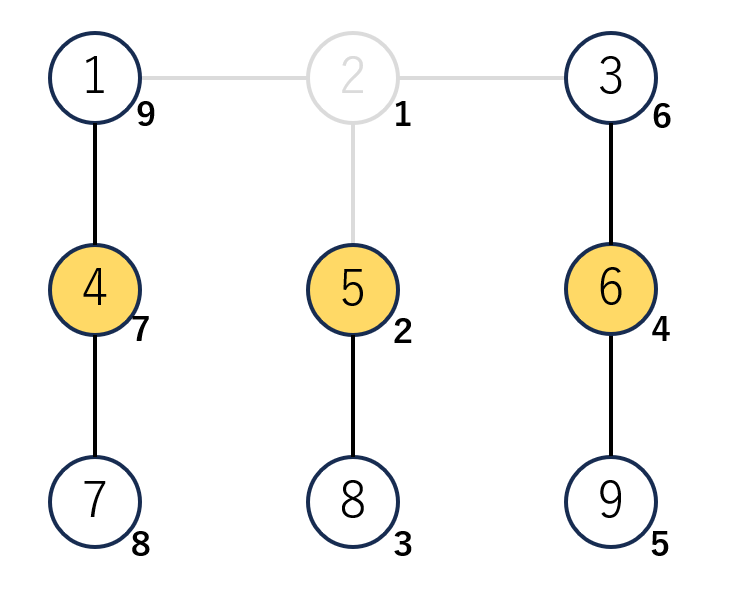
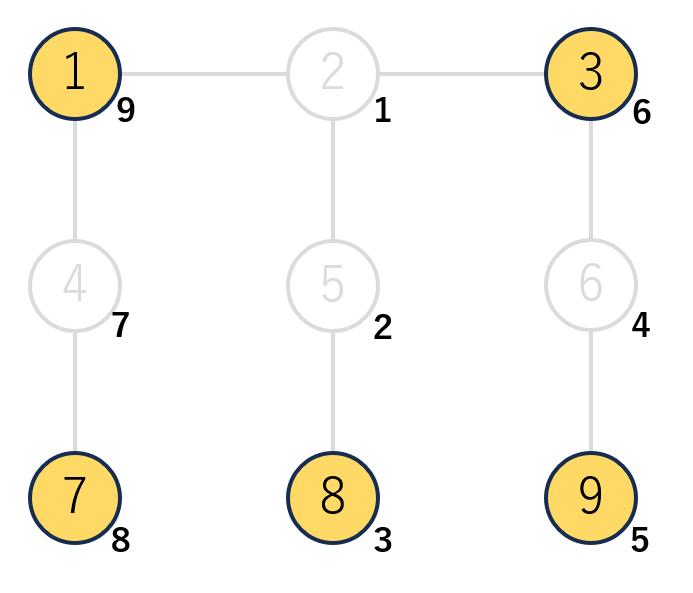
ここで、頂点1を通過する長さ2のパスを数え上げることを考えます。
頂点1を通過する長さ2のパスは3通りあるのですが、これらは頂点1が所属する$O(logN)$個の重心木のみを考えれば解くことが可能です。
具体的には、「重心2を通過する2通りのパス」「重心4を通過する1通りのパス」「重心1を通過する0通りのパス」と数えればよいです。
このように、パスクエリを根つき木の問題に落とし込めるのが重心分解の強みです。
実装例・使い方
実装にあたって問題になるのが、Pythonの遅さです。
具体的には再帰の遅さと、連想配列・集合管理の遅さが課題になります。
前者は非再帰DFS、後者は連想配列を一切使わないことで対処しています。
非再帰DFSはKiri8128さんの記事が大変参考になります。
連想配列を避ける方法ですが、重心の決定順を採番するだけで達成可能です。
これは、重心木を再帰的に小さく分割するアルゴリズムが関係しています。
- 重心から連続する頂点のうち、自身よりも決定順が先の頂点は再帰元の重心
- 自身よりも決定順が後の頂点は、すべて自分より後に再帰分割された子の頂点
という図式が成り立つからです。
実際、上の図でもこれらが成り立つことが確認できます。
頂点の右下に書き込まれた、重心の決定順に注目します。
- 重心木内では、重心の決定順が最も早く、子の決定順は常に遅い
- 重心木から外につながる頂点の決定順は、重心の決定順よりも常に早い
ことが確認できます。
下の実装例ではorder[c]の配列に重心の決定順を格納しています。
重心cの重心木に属する頂点群を取得したいときは、重心cからBFS・DFSを行い、order[c] <= order[v]を満たす頂点vを列挙すればよいです。
class Centroid_decomposition:
def __init__(self, N: int, G: list[int]):
#頂点数N, 隣接リストGを渡す。重心分解を行う
#order[c]: 重心分解後の部分木における、重心cのDFS到達順
# 重心cの部分木は、orderが重心cよりも「大きい」BFSで移動可能な頂点
#depth[c]: 重心分解後の部分木における、重心cの深さ
#belong[c]: 重心分解後の部分木における、重心cの親となる重心(根の場合、-1)
# belong[c]を再帰的にたどることで、頂点iが属する重心を列挙できる
self.N = N
self.logN = N.bit_length()
self.order = order = [-1] * N
self.depth = depth = [-1] * N
self.belong = belong = [-1] * N
#部分木の大きさを前計算
stack, size = [(0, -1)], [1] * N
for now, back in stack:
for nxt in G[now]:
if nxt != back:
stack.append((nxt, now))
while stack:
now, back = stack.pop()
if back != -1:
size[back] += size[now]
#重心分解を実行
stack = [(0, -1, 0)]
for c in range(N):
now, back, d = stack.pop()
#1. 重心を探す
while True:
for nxt in G[now]:
if order[nxt] == -1 and size[nxt] * 2 > size[now]:
size[now], size[nxt], now = size[now] - size[nxt], size[now], nxt
break
else: #forループが完走 = 頂点nowが重心の場合
break
#2. 採番
order[now], depth[now], belong[now] = c, d, back
#3. 重心に隣接する頂点を再帰的に重心分解
if size[now] > 1:
for nxt in G[now]:
if order[nxt] == -1:
stack.append((nxt, now, d + 1))
#頂点u, vをどちらも含む、最も小さい部分木の重心を返す
def find(self, u: int, v: int):
du, dv = self.depth[u], self.depth[v]
for du in range(du - 1, dv - 1, -1):
u = self.belong[u]
for dv in range(dv - 1, du - 1, -1):
v = self.belong[v]
while u != v:
u, v = self.belong[u], self.belong[v]
return u
#頂点vが属する重心木を、サイズの昇順に列挙する
def get(self, v: int):
vertices = []
for d in range(self.depth[v], -1, -1):
vertices.append(v)
v = self.belong[v]
return vertices
使用例
重心分解の使用例です。
定数倍高速化のため、連想配列は極力避けた実装をしています。
ABC291Ex Balanced Tree
問題文はこちら
最小共通祖先をパス上に残しつつ、部分木が半分以下になり続ける木を構築してください。
解法
重心分解し、重心の再帰元を親とした木を構築すると条件を満たす木になります。
重心cの再帰元は配列belong[c]に入っているので、これを出力すればよいです。
実装例: 重心分解 (214ms)
ABC014D 閉路
問題文はこちら
2頂点(Ai, Bi)のパス長 + 1を出力してください。
解法
重心分解を行い、各重心木ごとに重心からの距離を前計算することを考えます。
dist[c][v]: 重心cから頂点vまでの距離
として連想配列を呼び出してもよいですが、今回は別の管理法を行います。
重心の深さdtを、自身が重心になるまでに呼び出した再帰の回数と定義します。
するとdtは$O(logN)$なので、これをキーとすることで連想配列を回避できます。
dist[v][dt]: 頂点vが属する深さdtの重心cの、重心cから頂点vまでの距離
とすると、空間計算量$O(NlogN)$で処理が可能です。
#dist[v][dt]: 頂点vの所属する重心木で、重心の深さがdt(dt = CD.depth[c])のものについて、
# 重心cから頂点vまでの距離
dist = [[0] * CD.logN for _ in range(N)]
#重心分解木でBFSを行い、dist[i][dt]を埋める
for c in range(N):
dt = CD.depth[c]
stack = [(c, -1, 0)]
while stack:
now, back, d = stack.pop()
dist[now][dt] = d
for nxt in G[now]:
if nxt != back and CD.order[c] <= CD.order[nxt]:
stack.append((nxt, now, d + 1))
なお、本問題はHL分解やLCAを用いることでも解くことが可能です。
重心分解は動作が遅いので、可能な限り避ける方が無難です。
実装例: 重心分解 (738ms), HL分解 + Sparse Table (741ms), 線形LCA (429ms)
みんなのプロコン2018 決勝C 木の問題
問題文はこちら
頂点$V_i$からの距離が$K_i$である頂点の個数を求めてください。
解法
重心分解を行い、以下の部分問題に帰着させます。
$n$頂点の木があり、根は頂点$c$です。
$O(n + q)$時間で、$q$個のクエリを処理してください。頂点$V_i$からの距離が$K_i$で、かつ根$c$を通るものの個数を求めよ。
この部分問題はDFSで解くことが可能です。
$V_i$から$v$のパスを$V_i$から根$c$・根$c$から$v$の2つに分割し、この総和が$K_i$となるような$v$の個数を数えればよいです。
ただし根を通らないパスを数えてしまわないよう、適切に減算処理が必要なので注意してください。
合計の計算量は$O((N+Q)logN)$になります。
なお、事前にグローバル変数に配列を定義しておき、毎回同じ配列を使い回すことで、連想配列を回避できます。
Pythonだと連想配列の有無で実行時間が倍変わるので、できる限り配列を使い回す実装を行いましょう。
実装例: 配列使い回し (1097ms), 連想配列使用 (2179ms)
ABC267F Exactly K Steps
問題文はこちら
頂点$V_i$からの距離が$K_i$である頂点をひとつ出力してください。
解法
重心分解でも一応解くことが可能です。
基本方針は上記の『木の問題』と同様で、頂点数を持つ代わりに具体的な頂点を高々2個持っておけばよいです。
ただし、Pythonだと定数倍高速化を相当に頑張らないと通りません。
実装例: 重心分解 (1992ms)
ABC202E Count Descendants
問題文はこちら
$U_i$の部分木であって、根からの距離が$D_i$のものの個数を求めてください。
強化版を考えます。
$N$頂点の根つき木があります。$Q$個のクエリを処理してください。
$i$番目のクエリでは$R_i$, $U_i$, $D_i$を与えるので、dist($R_i$, $v$) $= D_i$ かつ $R_i$~$v$パス中に$U_i$が存在する$v$の個数を出力してください。
解法
このままでは手がつけられないので、重心分解を行って以下の部分問題に帰着させます。
$n$頂点の木があり、根は頂点$c$です。
$O(n + q)$時間で、$q$個のクエリを [1] ~ [3]の順に処理してください。($R_i$, $U_i$, $D_i$)を与える。$R_i$, $U_i$は木内に存在することが保証される。
[1] dist($c$, $R_i$)を求めよ。
[2] $R_i$, $U_i$と$c$の位置関係により、クエリを3パターンに分類せよ。
(1) $R_i = c$ または LCA($R_i$, $U_i$)$= c$
(2) $U_i$の部分木中に$R_i$が存在する
(3) それ以外: $R_i$の部分木中に$U_i$が存在、LCA($R_i$, $U_i$)$≠ c$など[3] $d = D_i -$ dist($c$, $R_i$)とする。答えへの寄与を計算せよ。
(1) $U_i$の部分木内であって、距離が$d$の頂点数
(2) 重心木内で距離$d$の頂点数から、$c$→$U_i$方向の部分木で距離$d$の頂点数を減じた値
(3) 0
帰着後の問題は場合分けが多い根つき木の問題となります。
上記の『木の問題』よりも複雑ですが、適切に行うことでいずれも線形時間で解くことが可能です。
そして$Σn = O(NlogN)$かつ$Σq = O(QlogN)$なので、合計で$O((N+Q)logN)$で解くことができました。
実装例: 重心分解 (1654ms)
全国統一プログラミング王決定戦2019 本戦G Greatest Journey
$V_i$から始まる長さ$L_i$のウォークの重み総和の最大値を求めてください。
解法
答えは常に 最短パス + 0回以上の辺の往復 という形で表すことができます。
なので重心分解を行い、最短パスの部分を重心を必ず通るパスに読み替えます。
帰着後の部分問題はこのようになります。
$n$頂点の木があり、根は頂点$c$です。
準線形時間で、$q$個のクエリを [1] ~ [3]の順に処理してください。($V_i$, $L_i$)を与える。$V_i$は木内に存在することが保証される。
[1] 重心$c$からの距離と重み、$dist_{V_i}$, $cost_{V_i}$を求めよ。
[2] 各辺について、端点のうち重心$c$に近い側の頂点を$S_i$とする。
($S_i$, $C_i$)の組をすべて求め、$dist_{S_i}$順に並び替えよ。
[3] 各クエリにおいて、$x = L_i - dist_{V_i}$とする。
$x < 0$ または$x < dist_{S_i}$なら答えを0とする。それ以外の場合は、
$max( C_i x - dist_{S_i} C_i + cost_{S_i}) + cost_{V_i}$を求めよ。
[1]と[2]は単純なBFSで求めることが可能です。
[3]は線分追加・区間最大値であり、$O(qlog^2 n)$時間かければLi Chao Treeで解けます。
このままだと計算量が厳しいですが、クエリを$x$の昇順でソートすることで線分追加ではなく直線追加にできるため、$O((n + q)logn)$時間に減らすことが可能です。
実装例: 重心分解 (3729ms)
おわりに
おわりです。
じゅうしんぶんかいはおもしろいなとおもいました。





