ニューラルネットワークを0から自作＆MNIST手書き文字を学習＆PyTorchのモデルと比較

勉強のため、ニューラルネットワークを0から作ることにしました。
目標はみんな大好き(諸説あり)MNISTの手書き文字データベースの学習です。

とりあえずシンプルにやってみる

ニューラルネットワークのクラス作成

だいたい手動で書きます。

パラメータの初期化は適当な範囲でランダムでしたが、Xavier初期化を使うのが良いらしいのでそっちにしました。乱数の範囲を変更するだけなので特に難しいことはないです。
活性化関数は隠れ層がReLU、出力層はsoftmaxです。
損失関数はクロスエントロピーです。
最適化手法は一旦勾配降下法でやってみます。あとで比較したいので。

import numpy as np
import math


class NN:
    def __init__(self, input_dim, hidden_dim, output_dim):
        # 重み
        # Xavier初期化を使用
        limit_ih = np.sqrt(6 / (input_dim + hidden_dim))
        self.w_ih = np.random.uniform(-limit_ih, limit_ih, (hidden_dim, input_dim))
        limit_ho = np.sqrt(6 / (hidden_dim + output_dim))
        self.w_ho = np.random.uniform(-limit_ho, limit_ho, (output_dim, hidden_dim))

        # 通常の初期化の場合
        # self.w_ih = np.random.uniform(-0.5, 0.5, (hidden_dim, input_dim))
        # self.w_ho = np.random.uniform(-0.5, 0.5, (output_dim, hidden_dim))

        # バイアス
        self.b_h = np.zeros(hidden_dim)
        self.b_o = np.zeros(output_dim)

        # 活性化関数
        self.actv_func = np.vectorize(self._ReLU)
        self.actv_func_output = self._softmax

    def print_parameters(self):
        np.set_printoptions(suppress=True, precision=4)
        print("---------")
        print("input-hidden weight:")
        print(self.w_ih)
        print()
        print("hidden bias:")
        print(self.b_h)
        print()
        print("hidden-output weight:")
        print(self.w_ho)
        print()
        print("output bias:")
        print(self.b_o)
        print("---------")

    # -----------------------------------
    # activation function
    # -----------------------------------
    def _ReLU(self, x: float) -> float:
        return max(0, x)

    def _ReLu_d(self, x: float) -> float:
        if x > 0:
            return 1
        else:
            return 0

    def _softmax(self, x):
        e_x = np.exp(x - np.max(x))
        return e_x / e_x.sum(axis=0)

    # -----------------------------------
    # loss function
    # -----------------------------------

    def _cross_entropy(self, y_pred, y_true):
        # y_pred: ソフトマックス出力 (確率分布)
        # y_true: ワンホットラベル
        # 小さな値を加えて log(0) を防止
        epsilon = 1e-12
        y_pred = np.clip(y_pred, epsilon, 1.0 - epsilon)
        return -np.sum(y_true * np.log(y_pred))

    def _cross_entropy_grad(self, y_pred, y_true):
        # クロスエントロピーとソフトマックスの勾配
        return y_pred - y_true

    # -----------------------------------
    # forward
    # -----------------------------------
    def _calc_one(self, x):
        z_hidden = self.w_ih @ x + self.b_h
        a_hidden = self.actv_func(z_hidden)
        z_output = self.w_ho @ a_hidden + self.b_o
        y = self.actv_func_output(z_output)
        return y, z_output, a_hidden, z_hidden

    def _calc_one_simple(self, x):
        return self._calc_one(x)[0]

    def calc(self, x_mat):
        return np.apply_along_axis(self._calc_one_simple, 1, x_mat)

    # -----------------------------------
    # train
    # -----------------------------------
    def train(self, x_mat, t_mat, alpha=0.1, epochs=100):

        losses = []

        for i in range(epochs):

            # forward
            y_mat = self.calc(x_mat)

            # 損失を計算
            # loss = self._mse(y_mat, t_mat)
            loss = np.mean([self._cross_entropy(y, t) for y, t in zip(y_mat, t_mat)])
            print(f"ep.{i} loss: {loss}")
            losses.append(loss)

            # sigmoid_d = np.vectorize(self._sigmoid_d)
            ReLU_d = np.vectorize(self._ReLu_d)

            dL_dw_ho_list = []
            dL_dw_ih_list = []
            dL_db_o_list = []
            dL_db_h_list = []

            # back
            for x, t in zip(x_mat, t_mat):

                y, z_output, a_hidden, z_hidden = self._calc_one(x)

                # 勾配を計算
                # dL/dy
                # dL_dy = y - t

                # # dL/d(z_output)
                dL_dz_output = self._cross_entropy_grad(y, t)
                # dL_dz_output = dL_dy * sigmoid_d(z_output)
                # dL_dz_output = dL_dy * ReLU_d(z_output)

                # dL/d(w_ho)
                dL_dw_ho = np.outer(dL_dz_output, a_hidden)

                # dL/d(b_o)
                dL_db_o = dL_dz_output

                # dL/d(a_hidden)
                dL_da_hidden = self.w_ho.T @ dL_dz_output

                # dL/d(z_hidden)
                # dL_dz_hidden = dL_da_hidden * sigmoid_d(z_hidden)
                dL_dz_hidden = dL_da_hidden * ReLU_d(z_hidden)

                # dL/d(w_ih)
                dL_dw_ih = np.outer(dL_dz_hidden, x)

                # dL/d(b_h)
                dL_db_h = dL_dz_hidden

                # 勾配を記録
                dL_dw_ho_list.append(dL_dw_ho)
                dL_dw_ih_list.append(dL_dw_ih)
                dL_db_o_list.append(dL_db_o)
                dL_db_h_list.append(dL_db_h)

            # 勾配の平均を取る
            dL_dw_ho_avg = sum(dL_dw_ho_list) / len(x_mat)
            dL_dw_ih_avg = sum(dL_dw_ih_list) / len(x_mat)
            dL_db_o_avg = sum(dL_db_o_list) / len(x_mat)
            dL_db_h_avg = sum(dL_db_h_list) / len(x_mat)

            # 勾配を更新する
            self.w_ho -= alpha * dL_dw_ho_avg
            self.w_ih -= alpha * dL_dw_ih_avg
            self.b_o -= alpha * dL_db_o_avg
            self.b_h -= alpha * dL_db_h_avg

        return losses

MNISTデータを入力して学習してみる

このへんはAIに頼ってコード書きました。

from sklearn.datasets import fetch_openml
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

mnist = fetch_openml("mnist_784")

# 入力データをfloat型に変換し、[0,1]にスケーリング
x = mnist["data"]  # 特徴量: 70000 x 784
x = x.to_numpy().astype(np.float32) / 255.0

# ターゲットをint型に変換し、ワンホットラベルに変換
y = mnist["target"]  # ターゲット: 70000
y = y.astype(np.int64)
lb = LabelBinarizer()
y_onehot = lb.fit_transform(y)
# print("One-hot encoded targets shape:", y_onehot.shape)  # (70000, 10)
# print("Sample target:", y_onehot[0])  # 例: [0, 0, 0, 0, 0, 0, 0, 0, 0, 1] など

# データを訓練用とテスト用に分割
x_train, x_test, y_train, y_test = train_test_split(x, y_onehot, test_size=0.2, random_state=42)
# データを小さめにしておく
x_train, x_test, y_train, y_test = x_train[:1000], x_test[:1000], y_train[:1000], y_test[:1000]

# ニューラルネットワークの初期化
input_dim = 784  # 28x28ピクセル
hidden_dim = 128  # 任意の隠れユニット数
output_dim = 10  # 0-9の10クラス

nn = NN(input_dim, hidden_dim, output_dim)

# 初期状態の出力
print("Initial predictions:")
print(nn.calc(x_train[:5]))  # 最初の5サンプルの予測を表示

# 学習の実行
losses = nn.train(x_train, y_train, alpha=0.01, epochs=1000)
plt.plot(losses)

# 学習後の出力
print("\nPredictions after training:")
print(nn.calc(x_train[:5]))  # 最初の5サンプルの予測を表示

とりあえず学習率0.01の1000epochsでやります。

初期の損失は2.39でしたが、じわじわ下がっていって0.32くらいになりました。まだ落ちそうな雰囲気です。

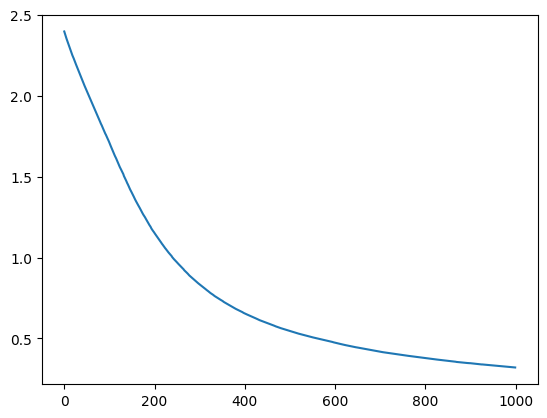
正解率を計算してみましょう。

# 正解率の計算
x_test_pred = nn.calc(x_test)
correct = 0
for y_true, y_pred in zip(y_test, x_test_pred):
    if np.argmax(y_true) == np.argmax(y_pred):
        correct += 1
accuracy = correct / len(y_test)
print(f"Accuracy: {accuracy:.4f}")
# -> Accuracy: 0.8630

86.3%でした。
お手製NNで学習できてて感動しますね♪

最適化手法を変更してみよう

学習が遅ーーーい！！！！！
ということで、最適化手法を勾配降下法からAdam最適化に変更してみます。
簡単に言えば勾配の方向だけでなく勾配を降りる速度と加速度も考慮してバーって降りてくれます。

修正した箇所

class NN:
    def __init__(self, input_dim, hidden_dim, output_dim):

        ...

        # Adam用の変数を初期化 (m: 1次モーメント, v: 2次モーメント)
        # w_ih, w_ho, b_h, b_o それぞれに対応させる
        self.m_w_ih = np.zeros_like(self.w_ih)
        self.v_w_ih = np.zeros_like(self.w_ih)
        self.m_w_ho = np.zeros_like(self.w_ho)
        self.v_w_ho = np.zeros_like(self.w_ho)

        self.m_b_h = np.zeros_like(self.b_h)
        self.v_b_h = np.zeros_like(self.b_h)
        self.m_b_o = np.zeros_like(self.b_o)
        self.v_b_o = np.zeros_like(self.b_o)

        # Adamステップカウンタ
        self.t_step = 0

    ...

    # -----------------------------------
    # train
    # -----------------------------------
    def train(self, x_mat, t_mat, alpha=0.01, epochs=1000, beta1=0.9, beta2=0.999, eps=1e-8):

        losses = []

        for i in range(epochs):

            ...

            # back
            for x, t in zip(x_mat, t_mat):

                ...

            # 勾配の平均を取る
            ...

            # 勾配を更新する(Adam最適化)
            # 時間ステップを増やす
            self.t_step += 1

            # 1) m, vを更新
            self.m_w_ho = beta1 * self.m_w_ho + (1 - beta1) * dL_dw_ho_avg
            self.v_w_ho = beta2 * self.v_w_ho + (1 - beta2) * (dL_dw_ho_avg**2)

            self.m_w_ih = beta1 * self.m_w_ih + (1 - beta1) * dL_dw_ih_avg
            self.v_w_ih = beta2 * self.v_w_ih + (1 - beta2) * (dL_dw_ih_avg**2)

            self.m_b_o = beta1 * self.m_b_o + (1 - beta1) * dL_db_o_avg
            self.v_b_o = beta2 * self.v_b_o + (1 - beta2) * (dL_db_o_avg**2)

            self.m_b_h = beta1 * self.m_b_h + (1 - beta1) * dL_db_h_avg
            self.v_b_h = beta2 * self.v_b_h + (1 - beta2) * (dL_db_h_avg**2)

            # 2) バイアス補正
            m_hat_w_ho = self.m_w_ho / (1 - beta1**self.t_step)
            v_hat_w_ho = self.v_w_ho / (1 - beta2**self.t_step)

            m_hat_w_ih = self.m_w_ih / (1 - beta1**self.t_step)
            v_hat_w_ih = self.v_w_ih / (1 - beta2**self.t_step)

            m_hat_b_o = self.m_b_o / (1 - beta1**self.t_step)
            v_hat_b_o = self.v_b_o / (1 - beta2**self.t_step)

            m_hat_b_h = self.m_b_h / (1 - beta1**self.t_step)
            v_hat_b_h = self.v_b_h / (1 - beta2**self.t_step)

            # 3) パラメータを更新
            self.w_ho -= alpha * m_hat_w_ho / (np.sqrt(v_hat_w_ho) + eps)
            self.w_ih -= alpha * m_hat_w_ih / (np.sqrt(v_hat_w_ih) + eps)
            self.b_o -= alpha * m_hat_b_o / (np.sqrt(v_hat_b_o) + eps)
            self.b_h -= alpha * m_hat_b_h / (np.sqrt(v_hat_b_h) + eps)

        return losses

再学習してAdam最適化の効果を見る

• alpha: 0.01
• epochs: 1000
• beta1: 0.9
• beta2: 0.999
• eps: 1e-8
  でとりあえずやってみます。

ep.0 loss: 2.370443769681269
ep.1 loss: 1.516563921164005
ep.2 loss: 0.9323801427131219
ep.3 loss: 0.6275790327589433
ep.4 loss: 0.48283226357400455
ep.5 loss: 0.3939854116078599
ep.6 loss: 0.3026116107340136 <- さっきのを超えた！
ep.7 loss: 0.268203376232306
ep.8 loss: 0.23126060398845033
ep.9 loss: 0.1890178066419458
ep.10 loss: 0.1660360597016134
...
ep.97 loss: 0.000838656473823524
ep.98 loss: 0.0008287292279804689
ep.99 loss: 0.0008189866821870846

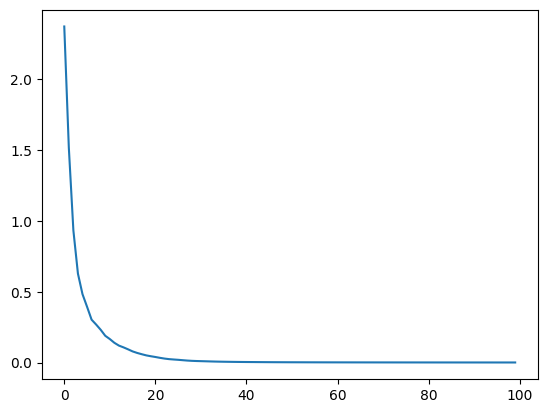
はえーーーーーー！！！！

最初の方は一気に勾配を降りることで、勾配降下法の1000epochsを5epochsくらいで駆け下りています。

早すぎて過学習起きそうなので100で一旦止めます。

同じように正解率を計算してみました。コードは同じです。

# 正解率の計算
x_test_pred = nn.calc(x_test)
correct = 0
for y_true, y_pred in zip(y_test, x_test_pred):
    if np.argmax(y_true) == np.argmax(y_pred):
        correct += 1
accuracy = correct / len(y_test)
print(f"Accuracy: {accuracy:.4f}")
# -> Accuracy: 0.8970

たった100epochで89%！流石です。

PyTorchと性能比較

PyTorchで同じようなモデルを作成して性能を比較してみます。
勝負だ！

PyTorchのコード

AIが作ってくれました。

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
from torch.utils.data import TensorDataset, DataLoader
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import numpy as np

# デバイスの設定（GPUが利用可能な場合はGPUを使用）
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"Using device: {device}")

# -----------------------------------
# データの取得と前処理
# -----------------------------------
# 〜このへん同じデータを使用するため省略〜

# 訓練データをさらに訓練と検証に分割
X_train, X_val, Y_train, y_val = train_test_split(x_train, y_train, test_size=0.1, random_state=42)

# NumPy配列からPyTorchのテンソルに変換
X_train_tensor = torch.from_numpy(X_train).to(device)
y_train_tensor = torch.from_numpy(Y_train).to(device)
X_val_tensor = torch.from_numpy(X_val).to(device)
y_val_tensor = torch.from_numpy(y_val).to(device)
X_test_tensor = torch.from_numpy(x_test).to(device)
y_test_tensor = torch.from_numpy(y_test).to(device)

# データローダーの作成
batch_size = 32

# 訓練データ
train_dataset = TensorDataset(X_train_tensor, y_train_tensor)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)

# 検証データ
val_dataset = TensorDataset(X_val_tensor, y_val_tensor)
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)

# テストデータ
test_dataset = TensorDataset(X_test_tensor, y_test_tensor)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)


# -----------------------------------
# モデルの定義
# -----------------------------------
class SimpleNN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SimpleNN, self).__init__()
        # 隠れ層
        self.hidden = nn.Linear(input_dim, hidden_dim)
        # 出力層
        self.output = nn.Linear(hidden_dim, output_dim)
        # 活性化関数
        self.relu = nn.ReLU()
        # SoftmaxはCrossEntropyLossに含まれるため、出力層に適用しない

    def forward(self, x):
        x = self.hidden(x)
        x = self.relu(x)
        x = self.output(x)
        return x


# モデルの初期化
input_dim = 784
hidden_dim = 128
output_dim = 10

model = SimpleNN(input_dim, hidden_dim, output_dim).to(device)


# Xavier初期化の適用
def init_weights(m):
    if isinstance(m, nn.Linear):
        nn.init.xavier_uniform_(m.weight)
        nn.init.zeros_(m.bias)


model.apply(init_weights)

# -----------------------------------
# 損失関数とオプティマイザの定義
# -----------------------------------
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

# -----------------------------------
# 学習ループ
# -----------------------------------
epochs = 100
losses = []
val_losses = []

start = time.time()
for epoch in range(epochs):
    model.train()
    epoch_loss = 0.0
    for batch_x, batch_y in train_loader:
        optimizer.zero_grad()
        outputs = model(batch_x)
        # ラベルをクラスインデックスに変換
        labels = torch.argmax(batch_y, dim=1)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        epoch_loss += loss.item()

    avg_epoch_loss = epoch_loss / len(train_loader)
    losses.append(avg_epoch_loss)

    # 検証損失の計算
    model.eval()
    val_loss = 0.0
    with torch.no_grad():
        for val_x, val_y in val_loader:
            val_outputs = model(val_x)
            val_labels = torch.argmax(val_y, dim=1)
            v_loss = criterion(val_outputs, val_labels)
            val_loss += v_loss.item()
    avg_val_loss = val_loss / len(val_loader)
    val_losses.append(avg_val_loss)

    print(f"Epoch {epoch+1}/{epochs} - Loss: {avg_epoch_loss:.10f} - Val Loss: {avg_val_loss:.4f}")
end = time.time()

# 損失のプロット
plt.figure(figsize=(10, 5))
plt.plot(range(1, epochs + 1), losses, label="Training Loss")
plt.plot(range(1, epochs + 1), val_losses, label="Validation Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training and Validation Loss over Epochs")
plt.legend()
plt.show()

print(f"Training time: {end-start:.2f}s")

# -----------------------------------
# テストデータでの評価
# -----------------------------------
model.eval()
correct = 0
total = 0
all_preds = []
all_labels = []
with torch.no_grad():
    for test_x, test_y in test_loader:
        outputs = model(test_x)
        _, predicted = torch.max(outputs.data, 1)
        labels = torch.argmax(test_y, dim=1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
        all_preds.extend(predicted.cpu().numpy())
        all_labels.extend(labels.cpu().numpy())

accuracy = correct / total
print(f"Test Accuracy: {accuracy:.4f}")

同じデータを使用して性能比較

学習データ・テストデータは同じものを使います。どちらも1000データです。

自作NNの結果

ep.0 loss: 2.341110687413803
ep.1 loss: 1.8180917652296766
ep.2 loss: 1.1057554505311677
ep.3 loss: 0.6784041047016736
ep.4 loss: 0.49165728939157716
ep.5 loss: 0.3684577475489058
...
ep.97 loss: 0.00043243791140777253
ep.98 loss: 0.000425435721947946
ep.99 loss: 0.0004178972507019465

Training time: 72.94s

Accuracy: 0.8820

1分ちょいくらいかかりました。

PyTorch版の結果

Epoch 1/100 - Loss: 0.9190644293 - Val Loss: 0.7317
Epoch 2/100 - Loss: 0.3420658559 - Val Loss: 0.6275
Epoch 3/100 - Loss: 0.1908886492 - Val Loss: 0.4529
Epoch 4/100 - Loss: 0.0939567947 - Val Loss: 0.7736
Epoch 5/100 - Loss: 0.0640264724 - Val Loss: 0.4409
...
Epoch 98/100 - Loss: 0.0000385177 - Val Loss: 0.7761
Epoch 99/100 - Loss: 0.0000358010 - Val Loss: 0.7806
Epoch 100/100 - Loss: 0.0000356147 - Val Loss: 0.7825

Training time: 1.90s

Test Accuracy: 0.9050

い、いってんきゅうびょう……？？

どうしてこんなに性能差があるのか？

AIによるとこういう感じらしいです。

学習時間の差は主に以下の要因によるものです：
-
ベクトル化と計算の最適化: PyTorchは内部で高度に最適化されたベクトル化演算を利用しており、計算速度が非常に速いです。自作NNではPythonループを多用しているため、計算速度が遅くなります。
オプティマイザの効率: PyTorchのAdamオプティマイザは高度に最適化されており、効率的にパラメータを更新できます。自作実装ではこれが遅くなる傾向があります。
自動微分の有無: PyTorchの自動微分機能は効率的に勾配を計算し、最適化を行います。一方、自作NNでは手動で勾配を計算しているため、計算効率が低下します。
精度の差については、PyTorchの高度な最適化や安定した数値計算が影響しています。自作NNでは、数値計算の微妙な違いやオプティマイザの実装の違いが精度に影響を与えている可能性があります。
-
改善策としては、ベクトル化の徹底やオプティマイザの最適化、NumPyの効率的な利用、あるいはCythonやNumbaの活用を検討することが考えられます。ただし、これらを自作NNに適用するのは時間と労力がかかるため、学習やプロトタイプの段階ではPyTorchなどのライブラリを活用することをお勧めします。

速度に関しては技術力不足でPythonループを排除できていないことが一番の要因だそうです。まあそうよな。
他にも各種計算が最適化されていたりC/C++で書かれていたりするらしいです。

やはりガチ勢には勝てないということです(？)

感想

勾配計算のところが特にわかってなかったので、手動で微分してコードに起こしてという過程を踏んで勉強になりました。
あと行列の扱いにまだ慣れてなくて何度かつまづきました。このへんは慣れておきたいですね。
最後に、よく使われるライブラリに勝負を挑むのは無謀なのでやめましょう(そらそう)。これだけ高性能なライブラリを無料で使えるのに感謝しながら使わせていただきましょう。