Go to Qiita Advent Calendar Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@naom1029

GBDT を MATLAB で実装してみた

Posted at

はじめに

機械学習のコンペティション（Kaggle など）で最強のアルゴリズムの一つと言われる GBDT (Gradient Boosting Decision Tree)。
今回は、その中身を深く理解するために、あえてライブラリを使わず MATLAB でゼロから実装してみました。

決定木とは「if 文の連続」である

実装に入る前に、そもそも決定木（Decision Tree）とは何かをプログラマ視点で考えてみます。
直感的に言えば、決定木は 「巨大な if 文の入れ子構造」 です。

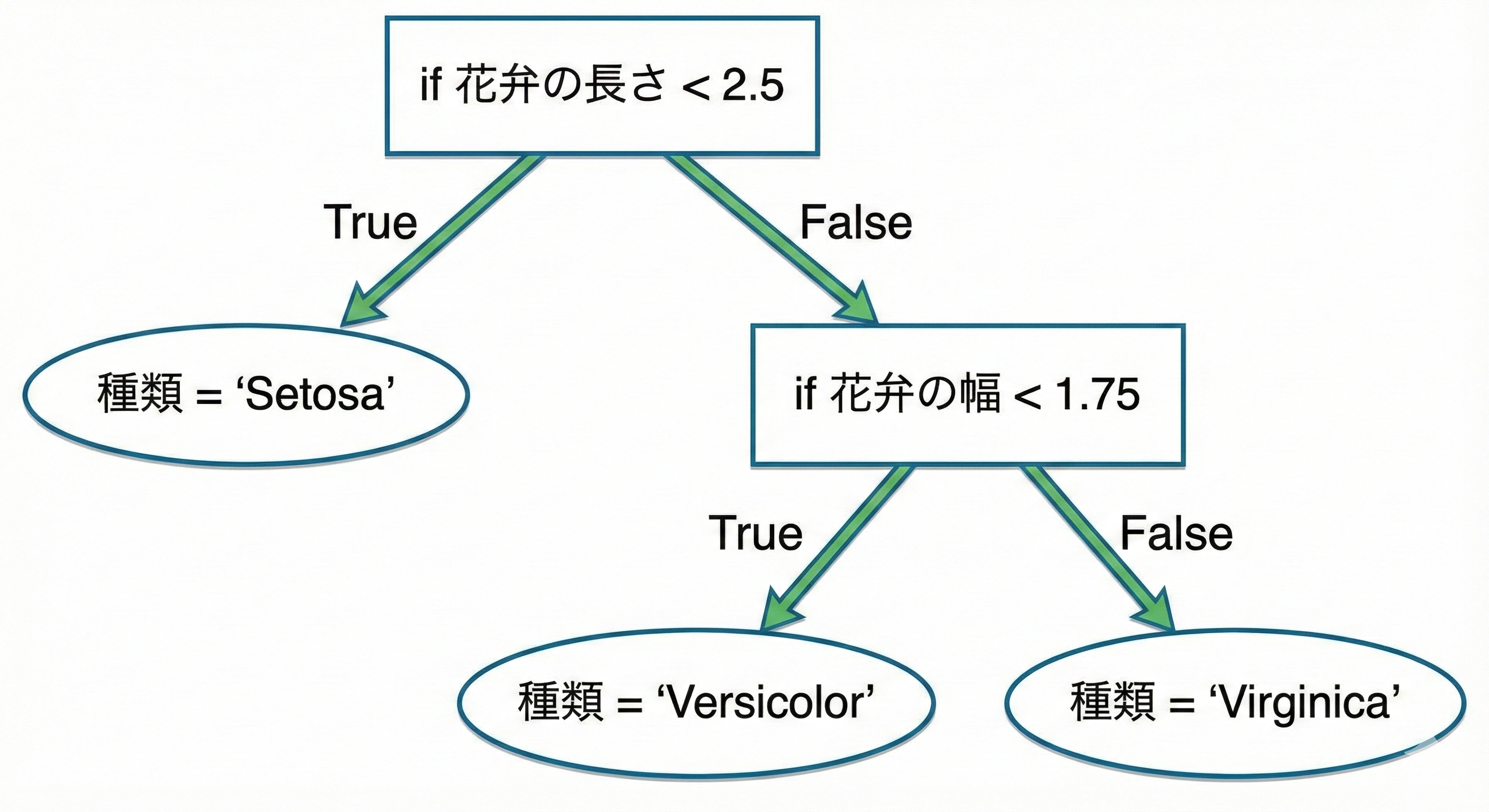
Decision Tree Example

例えば、ある花が「アヤメ（Iris）」のどの種類かを判定するプログラムを書くとします。

if 花弁の長さ < 2.5
    種類 = 'Setosa';
else
    if 花弁の幅 < 1.75
        種類 = 'Versicolor';
    else
        種類 = 'Virginica';
    end
end

このように、「ある特徴量が閾値より大きいか？」という条件分岐（if 文）を繰り返して最終的な答えに辿り着くのが決定木です。

GBDT の学習 ＝ 「if 文」を継ぎ足して賢くなる

では、GBDT はどうやって学習しているのでしょうか？
一言で言えば、「if 文の条件（閾値）を最適化しながら、if 文の塊（木）をどんどん継ぎ足していく」 ことで学習します。

  1. 閾値の最適化:
    「花弁の長さ < 2.5」の 2.5 という数字（閾値）は適当に決めているわけではありません。
    「どこで区切れば一番きれいにデータを分けられるか？」を計算し、最適な数値を見つけ出します。これが実装コードにある split 関数の役割です。

  2. if 文（木）の継ぎ足し:
    1 つの巨大な if 文ですべてを完璧に分類するのは大変です。
    そこで GBDT は、「前の if 文たちが間違えたところを修正するような、新しい if 文」 を次々に追加していきます。

    具体的には、「正解」と「今の予測」のズレ（残差） を次の木が予測するように学習します。
    例えば、正解が「30」のデータを予測する場合：

    • 1 本目: 「20」と予測（ズレは +10）
    • 2 本目: ズレの「+10」を予測しようとして、「+8」と予測（残りのズレは +2）
    • 3 本目: 残りのズレ「+2」を予測しようとして、「+1.5」と予測...

    最終的な予測は $20 + 8 + 1.5 = 29.5$ となり、正解に近づいていきます。
    これを繰り返すことで、最終的に非常に精度の高い「if 文の集合体」が出来上がります。

    ※厳密には、GBDT は「残差」そのものではなく、損失関数の負の勾配（Negative Gradient） を学習します。ただし、二乗誤差（回帰）の場合は負の勾配がちょうど「残差」と一致するため、直感的には「ズレを修正していく」という理解で問題ありません。

実装の概要

今回の実装の特徴は以下の通りです。

  • 言語: MATLAB
  • 手法: 2 階微分を用いた勾配ブースティング (Newton Boosting)
    • 通常の勾配降下法ではなく、XGBoost などで採用されているヘッセ行列（2 階微分）を利用した最適化を行っています。
  • 機能:
    • 回帰 / 2 値分類 / マルチクラス分類
    • 正則化 (L2 正則化 lambda, 葉の重みペナルティ gamma)

理論と実装の対応

GBDT では、目的関数を 2 次テイラー展開して近似し、それを最小化するように決定木を作成します。

1. 目的関数（損失関数）

今回は分類問題として、ロジスティック損失を使用しました。
2 階微分まで必要になるため、以下のように実装しています。

LogisticLoss.m
classdef LogisticLoss
    methods
        % ... (loss, gradは省略) ...

        % ヘッセ行列（2階微分）
        function ddcost = hess(obj,y,y_pred)
            prob = 1 ./ (1 + exp(-y_pred));
            ddcost = prob .* (1 - prob); % シグモイド関数の微分形
        end
    end
end

$\sigma(p)(1-\sigma(p))$ というシンプルな形になるのが美しいですね。

2. 木の成長と Gain の計算

決定木の「if 文の条件」を決める際、どこでデータを分割すれば最も予測精度が良くなるかを計算する必要があります。
これを評価するのが Gain（利得） です。

XGBoost の論文 (1) に出てくる「構造スコア」を用いた Gain の計算式をそのまま実装しました。

$$
Gain = \frac{1}{2} \left[ \frac{G_L^2}{H_L+\lambda} + \frac{G_R^2}{H_R+\lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda} \right] - \gamma
$$

  • $G_L, G_R$: 左/右の子ノードに含まれるデータの勾配の和
  • $H_L, H_R$: 左/右の子ノードに含まれるデータのヘッセ行列の和
  • $\lambda, \gamma$: 正則化パラメータ
Tree.m
function gain = CalcGain(obj,gl,hl,gr,hr)
    Gl = sum(gl); Hl = sum(hl);
    Gr = sum(gr); Hr = sum(hr);

    % 分割した時の左右のノードの評価関数が分割前より小さくなっていること
    gain = (Gl^2 / (Hl + obj.regLambda) + Gr^2 / (Hr + obj.regLambda) ...
           - (Gl + Gr)^2 / (Hl + Hr + obj.regLambda)) / 2 - obj.gamma;
end

この Gain が最大になる特徴量と閾値を探し出し、そこに if 文（分岐）を作ります。

3. 最適な分割点の探索 (split 関数)

Gain の計算式を使って、実際に最適な分割点（閾値）を探すのが split メソッドです。
この関数は、決定木の学習において最も計算時間を要する部分です。

Tree.m
% 閾値(分割点)を求める
function [best,threshold] = split(obj,node,grad,hess)
    X = node.X;
    bestGain = 0;
    best = [];
    threshold = [];

    for feature=node.features % 特徴量ごとにループ
        % ... (省略: 値が1種類しかない場合はスキップ) ...

        XX = X(:,feature);
        [~, ix] = sortrows(XX); % 特徴量でデータをソート
        x = X(ix,feature);
        grad = grad(ix);
        hess = hess(ix);

        % 計算量削減のため累積和 (O(N)で計算可能に)
        cgrad = cumsum(grad);
        chess = cumsum(hess);

        for i = 2:length(x)
            if x(i) == x(i-1); continue; end

            % 累積和を使って左右の勾配・ヘッセ和を高速に計算
            gl = cgrad(i - 1);
            hl = chess(i - 1);
            gr = cgrad(end) - cgrad(i - 1);
            hr = chess(end) - chess(i - 1);

            gain = obj.CalcGain(gl,hl,gr,hr);

            if gain > bestGain
                best = feature;
                threshold = (x(i) + x(i - 1)) / 2;
                bestGain = gain;
            end
        end
    end
end

ここでは 累積和 (cumsum) を使う工夫をしています。
通常、分割点をずらすたびに左右の勾配の和($G_L, G_R$)を計算し直すと時間がかかりますが、事前に累積和を計算しておくことで、各分割点での計算を $O(1)$ で行えるようにしています。

マルチクラス分類への拡張

GBDT 自体は回帰木（数値を予測する木）ですが、Iris データセットのような多値分類に対応させるため、One-vs-Rest アプローチを採用しました。
クラスの数だけ GBDT モデルを作成し、それぞれのクラスである確率（スコア）を予測させます。

GBDT_multiclass.m
function obj = fit(obj,X,y)
    n_classes = length(unique(y));
    for k=0:n_classes - 1
        y_k = (y == k); % クラスkかどうかの2値問題に変換
        % ... モデル学習 ...
    end
end

実験結果：パラメータを変えるとどうなる？

Iris データセット（3 クラス分類）を用いて、パラメータが学習にどう影響するかを実験しました。

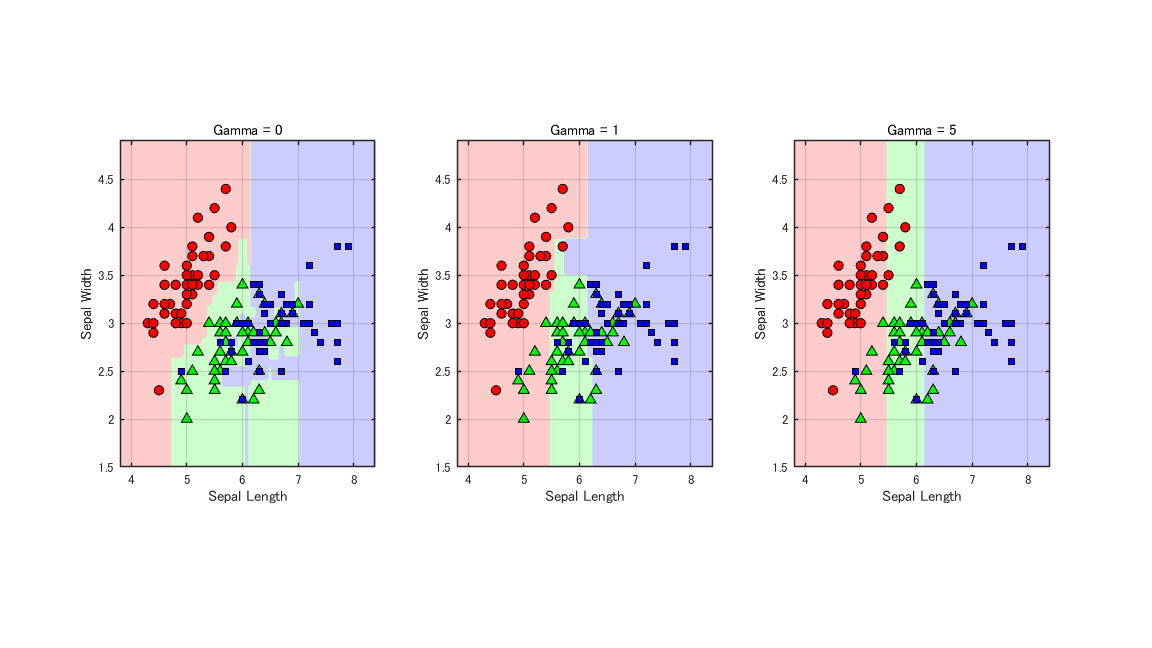
正則化パラメータ(gamma)と決定境界

gamma は「葉を増やすことに対するペナルティ」です。これを大きくすると、Gain が十分に大きくない分割が行われなくなるため、木がシンプルになります。

Decision Boundary with different Gamma

  • Gamma = 0: 複雑な境界線を描き、データ点に細かく合わせようとしています（過学習気味）。
  • Gamma = 1: 過学習を抑えつつ、データの分布をうまく捉えられています。今回のデータセットでは最もバランスが良い設定と言えそうです。
  • Gamma = 5: 境界線が滑らかでシンプルになっています。ただし、今回はシンプルになりすぎて分類精度が落ちてしまっているようにも見えます（アンダーフィット）。

まとめ

MATLAB で GBDT をスクラッチ実装することで、アルゴリズムの内部動作が非常によく理解できました。
特に、「if 文の条件」をどうやって自動的に決めているのか（Gain の最大化）、そのために勾配とヘッセ行列がどう使われているのかをコードレベルで追うことができました。

参考文献

(1) Tianqi Chen and Carlos Guestrin. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '16), 2016.

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?