こんにちは!Rustのイキリ構文オタクnamniumと申します ![]()
マイブームはRustのイイカンジな機能や構文を上手く活用してプログラムを書くことで、例えば let else 文とか while let 構文とか1を上手く組み込んでスッキリしたソースコードを書けた時にニマニマと笑ったりします!キモイ!そんなオタクですがよろしくお願いいたします ![]()
時に、paizaとQiitaがコラボキャンペーンを実施しているそうではないですか!(もう終了間際でしたが ![]() )
)
さかのぼること3、4年前、自分もRustで競プロに参加していました。(AtCoderの方ですが...) そんな思い出に浸りながらキャンペーン記事を読んでみると、同じくRustでキャンペーン記事を書いている人を見かけました。
競プロでRustを使うメリットはなんでしょうか...?やっぱり実行速度が速いから...?しかし競プロでは 速さだけ求めるならC++の方が楽そう です。競プロの解説はほとんどC++ですし、便利なツールもC++向けにはたくさん落ちている一方、Rustは競プロではまだまだ発展途上です。そして肝心の速度面ではどんなに頑張ったところでC++には勝てないでしょう。
Rustイキリ構文オタクの筆者に言わせればRustの 実行速度なんて飾りです 。Rustを競プロで使う理由...?そんなの決まってます! プログラムを美しく書けるから です!
今「え?」と思った読者の方も多いかもしれません。確かに、Rustは型に厳しかったり所有権・ライフタイムの存在のせいで時として膨大なソースコード量になることがしばしばで、知らない人からしたら読めなそうなコードばかりです。
Rustコードによる可読性の真価を感じるには、ある程度の学習コストを払わなければならないのは確かでしょう。しかし、一度読めるようになると別です。「ソースコードに 全部書いてるじゃん 」となるダニングクルーガーの完全理解山頂まで来ると、Rustに用意されている構文すべてがRustのパラダイムと噛み合っており、ソースコードに美しさを感じるようになるのです。本当です!
👨🔧「80%!?冗談じゃありません!現状で、Rustの性能は100%出せます!」
「速度が出てない」
👨🔧「あんなの飾りです!偉い人にはそれがわからんのですよ」
というわけで、競技プログラミングで使われる文脈では速度ばかりが注目されていそうなRustですが、今回は あえて機能や構文に注目 し、今回のpaizaキャンペーン問題を通して使用した面白イキリイディオムを緩く紹介していきたいなと思います!
広く使われている当たり前な機能も含まれるかもしれませんが、臆せず見せていきます。本記事を通して、読者の皆様に少しでもRustの魅力を伝えられれば幸いです。
あくまでもイディオムや機能紹介が主役なので、アルゴリズムの解説はあまりしません!モウシワケナイデス ![]()
![]()
それでは行きましょう!
自作標準入力関数【イキリ度☆☆☆☆★】
競プロで標準入力をどうやって受け取るかはどの言語でも最初に取り掛かるある種の問題でしょう。
RustでAtCoderに参加する場合だと、proconio という素晴らしいクレート(ライブラリのことです)を使用できますが、paizaではサードパーティ製のクレートは使用できないようです。
競プロで標準入力を受け取るならproconioがデファクトなのですが、素のRustで標準入力を受け取るには多少煩雑な処理を書く必要があります。
というわけで、本格的に問題に取り掛かる前に自前で標準入力用関数を用意することにしました!
- なるべくいろいろな入力で使いまわしたい
- マクロは処理が追いにくくなるからなるべく避けたい
以上2点を守って、こんな感じになりました。
use std::io::{BufRead, BufReader};
use std::str::FromStr;
use std::error::Error;
fn input<S, V>(stdin: &mut S) -> Result<V, Box<dyn Error>>
where
S: BufRead,
V: FromStr,
<V as FromStr>::Err: Error + 'static,
{
let mut line = String::new();
stdin.read_line(&mut line).map_err(Box::new)?;
let val: V = line.trim().parse().map_err(Box::new)?;
Ok(val)
}
たかが標準入力を受け取るごときでRustの面白機能 ジェネリクス を使ってしまいました...他の静的言語にもよくある機能ですね。ジェネリクスを使って書くことで、毎回問題ごとに標準入力関数を書き換える手間を省きました!
さっそく使い心地をD問題で確かめましょう。
問題文
整数 N が入力されるので、N 個の*を繋げた文字列を出力するプログラムを作成しましょう。
例えば N = 3の場合
***
のように出力してください。
N
Nは整数
4
筆者の回答
use std::io::{BufRead, BufReader};
use std::str::FromStr;
use std::error::Error;
fn input<S, V>(stdin: &mut S) -> Result<V, Box<dyn Error>>
where
S: BufRead,
V: FromStr,
<V as FromStr>::Err: Error + 'static,
{
let mut line = String::new();
stdin.read_line(&mut line).map_err(Box::new)?;
let val: V = line.trim().parse().map_err(Box::new)?;
Ok(val)
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n: usize = input(&mut stdin).unwrap();
println!("{}", "*".repeat(n));
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n: usize = input(&mut stdin).unwrap();
println!("{}", "*".repeat(n));
}
最初に出てくる let mut stdin = BufReader::new(std::io::stdin()); は標準入力を行単位で受け取るための某という感じです。 input<S, V>(...) 関数側ではジェネリクス S 型の値として受け取り、 where S: BufRead と指定することで、「行単位でバイトを吐きだす何かしらの入力(リーダー)」として扱える引数にしています。リーダーを可変参照として渡している( input 関数内で作り直したりしていない)のは、複数回 input 関数が呼ばれるケースの場合で、標準入力された文字がおかしな喰われ方をしないよう、一貫性を持たせて読み込むためです。
今回標準入力で与えられるのは BufReader<Stdin> だけなのでリーダーをジェネリクスにする必要はないのですが、一方で input 関数にとって入力が標準入力であるかには興味がないので関数内で入力の本質的な部分(BufRead トレイトが提供する機能)だけを抜き出す目的でジェネリクスとしました。
イキリポイント①
一般化しなくて良い箇所でわざわざジェネリクスを使い「俺は本質を見抜いてる ![]() 」と抜かす
」と抜かす
ジェネリクスであることがうまく機能しているのは input<S, V>(...) 関数のうちの型変数 V の方です。こちらは input 関数の返り値型を表しており、 line.trim().parse() の部分で文字列型を V 型の値に変換しています。 where V: FromStr という記述によって V 型として入ってくる型を FromStr トレイトを実装している、つまり文字列から変換して作成する機能を持つ型のみに限定しています。使用側では let n: usize = input(&mut stdin).unwrap(); として n: usize のように n の型を明示的に指定することで型推論させて V 型を usize であるとコンパイラに伝えています。 usize は FromStr を実装する型なので無事パースができます!
stdin.read_line(&mut line) ではメソッド名通り行単位の入力を行っています。 Box<dyn Error> 等については今回はブラックボックスで捉えてほしいのですが、 unwrap せず Result で返しているのはパニック( .unwrap() 等)をなるべく main 関数に集約するためです。このように書いておけば、パニックした際に一番先頭に表示される行番号が input 関数内ではなく呼び出し側の行になるのでデバッグがスムーズになります!
イキリポイント②
返り値型をResult型にすると嬉しい
前の問題では行全体で1入力だったので行を受け取り変換する input 関数を用意しましたが、スペース区切りで複数の入力が1行に与えられることもあります。こういう場合のためにベクトル(動的配列)を返してくれる input_vec 関数も用意しました。
use std::io::{BufRead, BufReader};
use std::str::FromStr;
use std::error::Error;
fn input_vec<S, V>(stdin: &mut S) -> Result<Vec<V>, Box<dyn Error>>
where
S: BufRead,
V: FromStr,
<V as FromStr>::Err: Error + 'static + Sized,
{
let mut line = String::new();
stdin.read_line(&mut line).map_err(Box::new)?;
let vals = line.trim()
.split(' ')
.map(|s| s.parse().map_err(Box::new))
.collect::<Result<Vec<V>, _>>()?;
Ok(vals)
}
input 関数とほぼ同じ感じですが、こちらの関数では split(' ') で文字列を区切り、 map(...) で各文字列を V 型の値に変換しています。
こちらの使い心地はこんな感じです。
問題文
2つの正の整数 a, b が半角スペース区切りで入力されるので a と b を足した数を出力してください。
※「掛け算」の問題では入力が改行区切りで与えられましたが、今回は半角スペース区切りで与えられます。
a b
1 1
筆者の回答
use std::io::{BufRead, BufReader};
use std::str::FromStr;
use std::error::Error;
fn input_vec<S, V>(stdin: &mut S) -> Result<Vec<V>, Box<dyn Error>>
where
S: BufRead,
V: FromStr,
<V as FromStr>::Err: Error + 'static + Sized,
{
let mut line = String::new();
stdin.read_line(&mut line).map_err(Box::new)?;
let vals = line.trim()
.split(' ')
.map(|s| s.parse().map_err(Box::new))
.collect::<Result<Vec<V>, _>>()?;
Ok(vals)
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let nums: Vec<usize> = input_vec(&mut stdin).unwrap();
println!("{:?}", nums.into_iter().sum::<usize>());
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let nums: Vec<usize> = input_vec(&mut stdin).unwrap();
println!("{:?}", nums.into_iter().sum::<usize>());
}
今回取り組んだ問題達は以上で紹介した input 関数と input_vec 関数があればとりあえず事足りました!というわけで問題を解いていきましょう!
match式のアームで遊ぶ 【イキリ度☆☆☆★★】
「Rustの強み」と言われてすぐに思いつくのはなんでしょうか?所有権?ライフタイム?
筆者的にはこの2つよりもまず「表現力豊かな型」、そしてそれに伴う「パターンマッチ」が先に上がると思っています。 Rustはパターンマッチを使いこなすのが9割 と言っても過言ではありません!(過言)
そんなわけで match 式のマッチアームはイキリRustaceanにとっては格好のターゲットなわけです。競プロでももちろん有効活用します!
パターンマッチは上から
問題文
今年もパイザ宝くじの季節がやってきました。パイザ宝くじ券には 100000 以上 199999 以下の 6 桁の番号がついています。毎年1つ当選番号 (100000 以上 199999 以下)が発表され、当たりクジの番号が以下のように決まります。
1等:当選番号と一致する番号
前後賞:当選番号の ±1 の番号(当選番号が 100000 または 199999 の場合,前後賞は一つしかありません)
2等:当選番号と下 4 桁が一致する番号(1等に該当する番号を除く)
3等:当選番号と下 3 桁が一致する番号(1等および2等に該当する番号を除く)
たとえば、当選番号が 142358 の場合、当たりの番号は以下のようになります。
1等:142358
前後賞:142357 と 142359
2等:102358, 112358, 122358, …, 192358 (全 9 個)
3等:100358, 101358, 102358, …, 199358 (全 90 個)
あなたが購入した n 枚の宝くじ券の各番号が入力されるので、それぞれの番号について、何等に当選したかを出力するプログラムを書いて下さい。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let b: usize = input(&mut stdin).unwrap();
let n: usize = input(&mut stdin).unwrap();
let numbers = (0..n).map(|_| input::<_, usize>(&mut stdin).unwrap());
for n in numbers {
let rank = match n {
m if m == b => "first",
m if m == b - 1 || m == b + 1 => "adjacent",
m if m % 10000 == b % 10000 => "second",
m if m % 1000 == b % 1000 => "third",
_ => "blank"
};
println!("{}", rank);
}
}
宝くじ当選で何等か出力する問題です。1等なのに2等と表示されないようにするため順番に気を付けなければならないですね。
他言語のswitch文等と同様に、Rustの match 式もパターンは上から検証していくため、アームの順番を1等から並べれば良いだけです。
let rank = match n {
m if m == b => "first",
m if m == b - 1 || m == b + 1 => "adjacent",
m if m % 10000 == b % 10000 => "second",
m if m % 1000 == b % 1000 => "third",
_ => "blank"
};
ここで m if m == b ではなく単に b と書けると嬉しいのですが、シャドーイングの関係で全て if ガードが必要になってしまっていますね。
match 式 (≠文)であるがゆえに、アーム先は "first" 等の返したい文字列だけを書けば rank 変数に束縛されるのがクールです ![]() C#等にも
C#等にも switch 式が導入されたりしていますが、Rustはこのような「式指向ブーム」の火付け役の一人なんじゃないかなと筆者は信じています。
タプルマッチ
パターンマッチは鍛えれば鍛えるほどネストを減らすことができわかりやすく条件分岐を書けるようになります。よくあるFizzBuzz問題がまさによさげな例です!
問題文
整数 N が入力として与えられます。
1からNまでの整数を1から順に表示してください。
ただし、表示しようとしている数値が、
・3の倍数かつ5の倍数のときには、"Fizz Buzz"
・3の倍数のときには、"Fizz"
・5の倍数のときには、"Buzz"
を数値の代わりに表示してください。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n: usize = input(&mut stdin).unwrap();
for i in 1..=n {
let res = match (i % 5, i % 3) {
(0, 0) => "Fizz Buzz".to_owned(),
(_, 0) => "Fizz".to_owned(),
(0, _) => "Buzz".to_owned(),
_ => i.to_string(),
};
println!("{res}");
}
}
宝くじと同じ解法を取ると、 if ガードにて余りが0かを検証する形になるのでこんな感じになりそうです。
let res = match i {
n if n % 15 == 0 => "Fizz Buzz".to_owned(),
n if n % 3 == 0 => "Fizz".to_owned(),
n if n % 5 == 0 => "Buzz".to_owned(),
n => n.to_string(),
};
しかしせっかくのパターンマッチ。 if ガードは減らしたいですね...こんな時はパターンマッチの構造を工夫します。FizzBuzzでは、タプルを使うことでカッコよく書けます ![]()
let res = match (i % 5, i % 3) {
(0, 0) => "Fizz Buzz".to_owned(),
(_, 0) => "Fizz".to_owned(),
(0, _) => "Buzz".to_owned(),
_ => i.to_string(),
};
タプルマッチから学べるのは、パターンマッチは割となんでも書けるということです。ここに他手続き型言語にはなさそうなRustの match 式の魅力があります。関数型の波動を感じる...!
イキリポイント③
関数型パラダイム由来な機能を積極的に使いたがる
パターンマッチで大活躍する直和型な enum があるのもそうですし、Haskell等モダンな関数型言語にありがちな強い型付け表現を見るとRustaceanは嬉しくなっちゃうんですね...
そして次の話題も関数型パラダイムがちょっと関わりそうな話です(←正直関わってないので「関数型パラダイム」って言いたいだけのイキリ)
繰り返し変数なら enumerate【イキリ度☆☆☆★★】
パターンマッチ以外でHaskellとかElixirとかその辺から来てそうな機能と言えばそう...遅延評価ですね!Rustのイテレータも map や filter 等が遅延評価(collect 等が呼ばれるまで何もしないよう)になっており、便利に扱えるメソッドが多々用意されています。
特に競プロで頻出そうで筆者お気に入りのメソッドがあります。 enumerate です!
問題文
あなたはこれから友人と N 回じゃんけんをします。しかし、あなたは全てを見通す千里眼の持ち主なので、友人がこれから出す N 回のじゃんけんの手が全て分かってしまいました。
ただただ全勝してしまうのは面白くないので、あなたは、N 回のじゃんけんで出した指の本数の合計がちょうど M 本になるようにじゃんけんをすることにしました。
このとき、あなたは最高で何回じゃんけんに勝つことができるでしょうか。
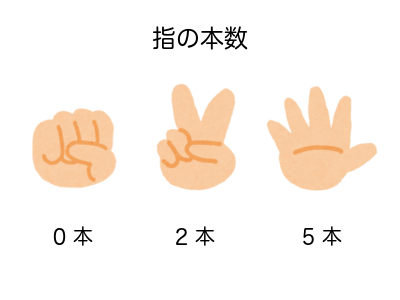
ここで、上の文中に出てくる「出した指の本数」というのは、じゃんけんで出した手の何本の指が立っていたか、ということであり、グー、チョキ、パーそれぞれ
・グー のとき ... 0 本
・チョキのとき ... 2 本
・パー のとき ... 5 本
の指を出していたということになります。
例えば、あなたが 4 回のじゃんけんで グー、パー、チョキ、グー と出したとすると、出した指の本数の合計は、
0 + 5 + 2 + 0 = 7
で 7 本となります。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
fn win_finger_num(f: char) -> usize {
match f {
'G' => 5,
'C' => 0,
'P' => 2,
_ => panic!("Invalid Finger"),
}
}
fn other_finger_num(f: char) -> (usize, usize) {
match f {
'G' => (0, 2),
'C' => (2, 5),
'P' => (5, 0),
_ => panic!("Invalid Finger"),
}
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n_m: Vec<usize> = input_vec(&mut stdin).unwrap();
let n = n_m[0];
let m = n_m[1];
let s: String = input(&mut stdin).unwrap();
let s: Vec<char> = s.chars().collect();
let max_fingers_num = n * 5;
// i手目までで、指の本数がjである場合の最大勝利数
let mut dp = (0..n + 1)
.map(|_| vec![0_usize; max_fingers_num + 1])
.collect::<Vec<_>>();
for (i, c) in s.into_iter().enumerate() {
let w_f = win_finger_num(c);
let (d_f, l_f) = other_finger_num(c);
for j in 0..=(i * 5) {
dp[i + 1][j + w_f] = dp[i + 1][j + w_f].max(dp[i][j] + 1);
dp[i + 1][j + d_f] = dp[i + 1][j + d_f].max(dp[i][j]);
dp[i + 1][j + l_f] = dp[i + 1][j + l_f].max(dp[i][j]);
}
}
println!("{}", dp[n][m]);
}
for (i, c) in s.into_iter().enumerate() {
let w_f = win_finger_num(c);
let (d_f, l_f) = other_finger_num(c);
for j in 0..=(i * 5) {
dp[i + 1][j + w_f] = dp[i + 1][j + w_f].max(dp[i][j] + 1);
dp[i + 1][j + d_f] = dp[i + 1][j + d_f].max(dp[i][j]);
dp[i + 1][j + l_f] = dp[i + 1][j + l_f].max(dp[i][j]);
}
}
enumerate の機能はシンプルで「イテレータ上のアイテムをインデックス付きで取り出す」というものです。しかしこの単純な機能が可読性を大いに上げるのです...!
enumerate を使わない場合で今回みたいにインデックスを活用したい時、 for i in 0..s.len() {...} として内側で let c = s[i]; とやって要素を取り出すことになりますが、これだとループ内で 繰り返し変数 i が s 由来であることがわかりにくい です。もちろん宣言部を見ればすぐわかる話ではありますが、認知が一瞬遅れます。一方で enumerate で繰り返していれば
- 範囲外アクセスの不安が少なくとも
s[i]の分についてはなくなる -
iがs由来でありかつ i番目がc であることが宣言部からすぐわかる
という感じでメリットしかありません。(感覚的な話なので言語化がムズイ...)
今回は enumerate を激推ししました。この他にもイテレータには数多くの便利なメソッドが用意されています。
そしてイテレータとその便利メソッド達を上手く活用することでほとんどの場合for文を使わずに綺麗にコレクション操作を行うことができます!"イテレータイキリ"としてはむしろこっちの方が日常茶飯事ですね ![]()
// forで回してpushは正直ダサい
/*
let mut dp = Vec::with_capacity(n + 1);
for _ in 0..(n + 1) {
dp.push(vec![0_usize; max_fingers_num + 1]);
}
*/
// i手目までで、指の本数がjである場合の最大勝利数
let mut dp = (0..n + 1)
.map(|_| vec![0_usize; max_fingers_num + 1])
.collect::<Vec<_>>();
イキリポイント④
for 文をいかに減らせるかの遊びをしたりする
ここまで熱く語ってきましたが、 map 、 enumerate 等のイテレータや遅延評価周りの話題は、Rustに限らずPythonやC#等様々な言語で見られます。とはいえ本節で言いたかったのは Rustにとってもイテレータは十八番 ということです!筆者は元Pythonistaなのですが、この辺の事情よりPythonから別言語への乗り換えを検討している方にRustはぜひオススメです!
ラベルジャンプ【イキリ度☆☆★★★】
今回解いた中でちょっと変わった機能である「ラベル」を使えたので紹介したいと思います!
問題文
東京の下町に長テーブルで有名な老舗うなぎ屋がありました。
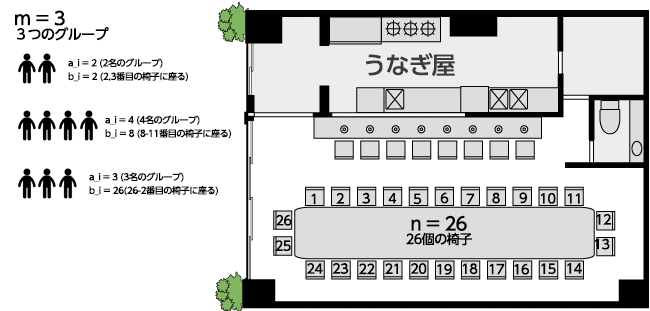
そのうなぎ屋にはとても大きい長テーブルがあり、テーブルの周りにn個の座席が配置されています。
座席には、時計回りに1, 2, …, nと番号が振られています。
座席はテーブルの周りに配置されているので、座席番号nの座席と1の座席は隣接しています。(下記図を参照の事)
今、m個のグループの人達が座席に順番に座りに来ます。i番目(1≦i≦m)のグループの人数をa_i人とします。
彼らは、長テーブルに並んだ座席の内、ある連続するa_i個の座席に一斉に座ろうとします。
ただしお客さんは江戸っ子なので、それら座席のうち、いずれか一つでも既に先客に座られている座席があった場合、
一人も座らずにグループ全員で怒って帰ってしまいます。江戸っ子は気が早いんでぃ。
入力では、i番目のグループが座ろうとする連続した座席の位置は、整数b_iにより指定されます。
i番目のグループは、座席番号b_iの座席を始点として、そこから時計回りにa_i個分の座席に座ろうとします。
最後のグループが座りに来た後、無事に長テーブルの座席に着席出来ている人数を出力するプログラムを作成してください。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n_m: Vec<usize> = input_vec(&mut stdin).unwrap();
let n = n_m[0];
let m = n_m[1];
let groups = (0..m).map(|_| {
let a_b: Vec<usize> = input_vec(&mut stdin).unwrap();
// 座席位置のインデックスを0オリジンにしておく
(a_b[0], a_b[1] - 1)
});
let mut sheets = vec![false; n];
let mut success_num = 0;
'group: for (a, b) in groups {
let mut try_sheets = sheets.clone();
for i in b..b + a {
if try_sheets[i % n] {
continue 'group;
}
try_sheets[i % n] = true;
}
sheets = try_sheets;
success_num += a;
}
println!("{success_num}");
}
この問題は「複数のグループがあり、さらにその中の誰かが座れなかったらグループごと帰る」という謎の江戸っ子たちの問題なのですが、要は「二重ループの外側へ continue 」があると便利な問題です。
なんとRustにはラベルジャンプが...あります!( continue や break 限定)
'group: for (a, b) in groups {
let mut try_sheets = sheets.clone();
for i in b..b + a {
if try_sheets[i % n] {
continue 'group; // 外側についてコンティニュー
}
try_sheets[i % n] = true;
}
sheets = try_sheets;
success_num += a;
}
continue 'group; によって外側のグループでのコンティニューができています。
一般に、ラベルジャンプは可読性を下げる恐れがあるのでアンチパターンとされていますが、ループから抜け出す時は許容されることが多いですよね。それを受けてかRustにも用意されてます!
さらにRustの場合は、所有権やライフタイムがコンパイラによって管理されているためにこの 無理なラベルジャンプをしても不都合が出にくい です。使うにあたり恐れるものは何もない...!
イキリポイント⑤ (?)
ラベルに適切な名前を付けられる時が筆者が地味に好きな瞬間です。
引数用構造体と分解構文 【イキリ度☆☆★★★】
Rustの構造体は他言語のクラス等と比べるとかなりカジュアルに使えます!タプルレベルでお手軽!
例えば「引数をグルーピングする」程度の用途で使っても何も不都合はなく、可読性を大いに向上させる機能です!
問題文
ハノイの塔というパズルがあります。
3つの杭があり、左から順にA,B,Cの杭とします。
杭Aに円盤が下から大きい順に n 個重なって置かれています。
この円盤は必ず1つ上の円盤は下の円盤より小さくなくてはいけないルールがあります。
このルールを守りながらAの杭からCの杭へ円盤を動かす操作をするパズルです。
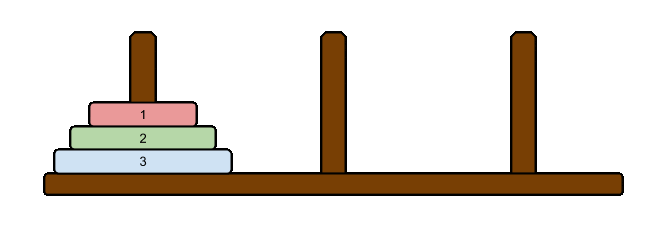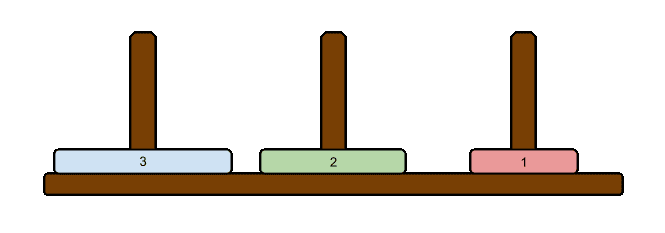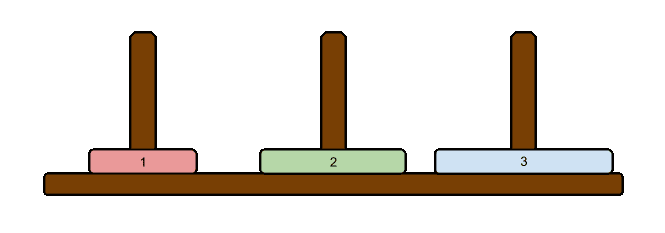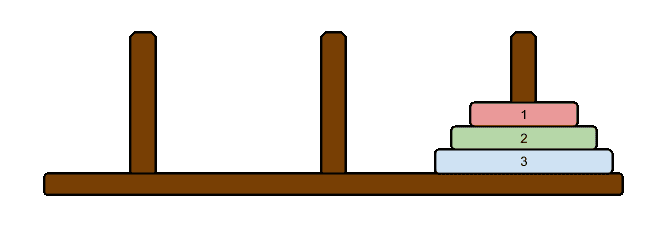
例えば3つの円盤が入力として与えられる場合、その時の最短手順は以下の通りになります。
この時、円盤の数に寄らず最短手順は常に一意に決まります。
円盤の数 n が与えられます。1つも動かしていない状態を t = 0 とし、円盤を動かした回数を t とします。
円盤の数 n と、円盤を動かした回数 t が与えられるので n 個の円盤を最短手順で動かしていった時に円盤を動かした回数 t の状態を出力してください。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
struct TargetPoll {
src: usize,
mid: usize,
dest: usize,
}
fn hanoi(tower: &mut [Vec<usize>; 3], poll: TargetPoll, m: usize, rest: &mut usize) {
if m == 0 || *rest == 0 {
return;
}
let TargetPoll { src, mid, dest } = poll;
hanoi(
tower,
TargetPoll {
src,
mid: dest,
dest: mid,
},
m - 1,
rest,
);
if *rest == 0 {
return;
}
let disc = tower[src].pop().unwrap();
tower[dest].push(disc);
*rest -= 1;
hanoi(
tower,
TargetPoll {
src: mid,
mid: src,
dest,
},
m - 1,
rest,
);
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n_t: Vec<usize> = input_vec(&mut stdin).unwrap();
let n = n_t[0];
let mut t = n_t[1];
let mut tower = [
(1..=n).rev().collect(),
Vec::with_capacity(n),
Vec::with_capacity(n),
];
hanoi(
&mut tower,
TargetPoll {
src: 0,
mid: 1,
dest: 2,
},
n,
&mut t,
);
for poll in tower {
let res: Vec<String> = poll
.into_iter()
.map(|disc| disc.to_string())
.collect::<Vec<_>>();
let res = if !res.is_empty() {
res.join(" ")
} else {
"-".to_string()
};
println!("{res}");
}
}
ハノイの塔は有名な再帰の問題ですね。
- まず、上に乗っている円盤を余った棒に移したことにする
- 対象の円盤を対象の棒に置く
- 余った棒に移した円盤を、対象の棒に置いたことにする
この「移したことにする」の部分が再帰のミソですが...まぁ今回注目してほしいのはそこではないです。
struct TargetPoll {
src: usize,
mid: usize,
dest: usize,
}
fn hanoi(tower: &mut [Vec<usize>; 3], poll: TargetPoll, m: usize, rest: &mut usize) {
if m == 0 || *rest == 0 {
return;
}
let TargetPoll { src, mid, dest } = poll;
hanoi(
tower,
TargetPoll {
src,
mid: dest,
dest: mid,
},
m - 1,
rest,
);
// ...
}
ハノイの塔の再帰関数の引数には「移動元、余った棒、移動先」があります。これだけで3つも引数を占拠しており、なおかつ今回のちょっと変わった(途中で停止させられる)ハノイの塔を解くには(もしかしたら不要かもしれませんが)移動回数を記録するための変数等他に注目したい引数が出てきたりします。
引数の数を減らしたい...というわけで、棒のインデックスを表すこの3つを、 TargetPoll 構造体にまとめてしまうことにしました!
struct TargetPoll {
src: usize,
mid: usize,
dest: usize,
}
fn hanoi(tower: &mut [Vec<usize>; 3], src: usize, mid: usize, dest: usize, m: usize, rest: &mut usize) {...}
↓
fn hanoi(tower: &mut [Vec<usize>; 3], poll: TargetPoll, m: usize, rest: &mut usize) {...}
読みやすい!ちなみに構造体から値を取り出す方法ですが、 poll.src みたいにいちいちアクセスしていると面倒です。Rustの構造体は分割代入みたいに変数を分割できるので、この機能を使って分解します!
let TargetPoll { src, mid, dest } = poll;
パターンマッチはこの構造体分割と似た機能だったりします。もとい、この分割代入はパターンが一つに定まっている(論駁不可能な)特殊なパターンマッチの例と捉えるとわかりやすいです!
くわしくは拙著を読んでほしいです: Rustのlet-else文気持ち良すぎだろ
ともかく、特にメソッドとかを生やさなくてもカジュアルに構造体を使える辺りもRustが好きな理由ですね。
イキリポイント⑥
隙あらば構造体。隙あらば列挙体。
2024/8/30 追記
コメントでいただきました通り、構造体は引数段階で分解することも可能です!うーん...カッコつけがすぎてカッコいい...
fn hanoi(tower: &mut [Vec<usize>; 3], TargetPoll {src, mid, dest}: TargetPoll, m: usize, rest: &mut usize) {...}
@higumachan725 ありがとうございます ![]()
無理やりトレイトで共通化【イキリ度☆★★★★】
カジュアルに使える構造体。これがあるからやってしまうのが、 競プロの問題で出てきた概念のモデル化です...モデルを丁寧にプログラムするのが楽しすぎて、「制限時間内に解く」のが苦手になってしまったのが筆者が競プロをやめてしまった理由だったりします...Rustに出会わない方が競プロ的には良かった...?
モデル化をするとできるだけ一般化・抽象化もしたくなるというものです。そうして過度なモデル作成をすると出てくるのが「トレイト」です。 絶対競プロには要らない!!
問題文
野球の各打者はストライクが 3 つたまるとアウトとなり、ボールが 4 つたまるとフォアボールとなります。
アウトあるいはフォアボールになると、この打者の番は終了します。
あなたはストライクとボールを判定してコールする審判です。
その場の状況に合わせて適切なコールを出しましょう。
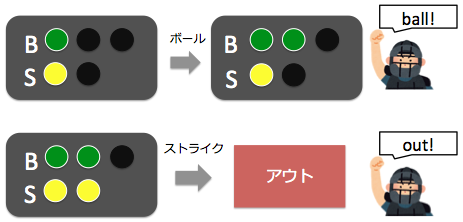
【コール一覧】
ストライクが 1 〜 2 つたまったとき → "strike!"
ストライクが 3 つたまったとき → "out!"
ボールが 1 〜 3 つたまったとき → "ball!"
ボールが 4 つたまったとき → "fourball!"
ある打者の番における投球の結果 (ストライクまたはボール) が与えられるので、各投球に対してどのようなコールをすればよいかを出力してください。
なお、実際の野球にあっても上記にないルール (ヒット、ファウルなど) については考慮する必要はありません。
1 球目: ボール → "ball!"
2 球目: ストライク → "strike!"
3 球目: ボール → "ball!"
4 球目: ストライク → "strike!"
5 球目: ストライク → "out!"
5 球目では、ボールが 2 つ、ストライクが 3 つたまったのでこの打者はアウトとなります。
これは、入力例 1 に対応しています。
1 球目: ボール → "ball!"
2 球目: ストライク → "strike!"
3 球目: ボール → "ball!"
4 球目: ボール → "ball!"
5 球目: ストライク → "strike!"
6 球目: ボール → "fourball!"
6 球目では、ストライクが 2 つ、ボールが 4 つたまったのでこの打者はフォアボールとなります。
これは、入力例 2 に対応しています。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
use std::marker::PhantomData;
trait Call {
fn full_count() -> usize;
fn normal_call() -> &'static str;
fn last_call() -> &'static str;
}
enum Counter<C: Call> {
Count(usize),
Exceeded(PhantomData<C>),
}
impl<C: Call> Counter<C> {
fn new() -> Self {
Self::Count(0)
}
fn count_up(&mut self) -> &'static str {
match self {
Self::Count(i) if *i < C::full_count() => {
*self = Self::Count(*i + 1);
C::normal_call()
},
_ => {
*self = Self::Exceeded(PhantomData);
C::last_call()
}
}
}
}
struct Strike;
impl Call for Strike {
fn full_count() -> usize {
2
}
fn normal_call() -> &'static str {
"strike"
}
fn last_call() -> &'static str {
"out"
}
}
struct Ball;
impl Call for Ball {
fn full_count() -> usize {
3
}
fn normal_call() -> &'static str {
"ball"
}
fn last_call() -> &'static str {
"fourball"
}
}
fn main() {
// 入力部
let mut stdin = BufReader::new(std::io::stdin());
let n: usize = input(&mut stdin).unwrap();
let judges = (0..n).map(|_| input::<_, String>(&mut stdin).unwrap());
// コール準備
let mut strike_counter = Counter::<Strike>::new();
let mut ball_counter = Counter::<Ball>::new();
for judge in judges {
let call = match judge.as_str() {
"strike" => strike_counter.count_up(),
"ball" => ball_counter.count_up(),
_ => "Invalid Judge",
};
println!("{}!", call);
}
}
野球の審判のコールをプログラムする問題です。
「ストライクカウンタ」も「ボールカウンタ」もフルカウントが異なるだけで仕組みは全く同一です。よって共通化しDRYにしたいです。一方でこれらを異なるカウンタとして具現化させたく、そのために(フルカウントをパラメータで持ったりせず)両者を型レベルで区別できるようにしたいです。
イキリポイント⑦
なんでも型にしたがる
というわけで「『カウンタ』それ自体の列挙体 Counter 」と、「『カウンタブルな概念』を表すトレイト Call 」を用意しました!やりすぎ
use std::marker::PhantomData;
trait Call {
fn full_count() -> usize;
fn normal_call() -> &'static str;
fn last_call() -> &'static str;
}
enum Counter<C: Call> {
Count(usize),
Exceeded(PhantomData<C>),
}
impl<C: Call> Counter<C> {
fn new() -> Self {
Self::Count(0)
}
fn count_up(&mut self) -> &'static str {
match self {
Self::Count(i) if *i < C::full_count() => {
*self = Self::Count(*i + 1);
C::normal_call()
},
_ => {
*self = Self::Exceeded(PhantomData);
C::last_call()
}
}
}
}
フルカウントかどうかでコールが変わるので、ここを match 式で切り替えています。それだけの列挙体です!なお、 Call については構造体実態は不要なので PhantomData を利用して型のみ保持できるようにしています。
trait Call {
fn full_count() -> usize;
fn normal_call() -> &'static str;
fn last_call() -> &'static str;
}
struct Strike;
impl Call for Strike {
fn full_count() -> usize {
2
}
fn normal_call() -> &'static str {
"strike"
}
fn last_call() -> &'static str {
"out"
}
}
struct Ball;
impl Call for Ball {
fn full_count() -> usize {
3
}
fn normal_call() -> &'static str {
"ball"
}
fn last_call() -> &'static str {
"fourball"
}
}
コールの方は「フルカウント」と「通常時のコール」「最後のコール」を得られるゲッターを用意しているだけで、こちらもシンプルです!
fn main() {
// 入力部
let mut stdin = BufReader::new(std::io::stdin());
let n: usize = input(&mut stdin).unwrap();
let judges = (0..n).map(|_| input::<_, String>(&mut stdin).unwrap());
// コール準備
let mut strike_counter = Counter::<Strike>::new();
let mut ball_counter = Counter::<Ball>::new();
for judge in judges {
let call = match judge.as_str() {
"strike" => strike_counter.count_up(),
"ball" => ball_counter.count_up(),
_ => "Invalid Judge",
};
println!("{}!", call);
}
}
丁寧なモデリングのお陰で可読性抜群な main 関数になったかと思います。特に let mut strike_counter = Counter::<Strike>::new(); のあたりは完成したプラモデルをじっくり観察しているみたいな気持ちになりますね...
自作リスト構造 【イキリ度★★★★★】
そして制限時間を気にせずモデリングすることが目的になると、まぁやりすぎちゃうことがままあるわけですね。今回のpaizaコラボキャンペーンで一番凝りすぎたと感じる問題はこちらです。
問題文
あなたは友達たちと N 人でしりとりを行うことにしました。
1 人目、 2 人目、...、 N 人目、 1 人目、2 人目、... という順序で発言をします。
ここで、それぞれの人は、次に挙げる 4 つのしりとりのルールを守って発言をする必要があります。
- 発言は、単語リストにある K 個の単語のうちのいずれかの単語でなければならない。
- 最初の人以外の発言の頭文字は、直前の人の発言の最後の文字と一緒でなければならない。
- 今までに発言された単語を発言してはならない。
- z で終わる単語を発言してはならない。
ここで、発言の途中で上のルールを破った場合、ルールを破った人はしりとりから外れます。
そして、その人を抜いて引き続きしりとりを続けていきます。このとき、後続の人は、ルール 2 を守る必要はありません。
N 人がしりとりを行ったログが M 行分与えられます。
このとき、M 回の発言が終わった後、しりとりから脱落せずに残っている人のリストを表示するプログラムを書いてください。
筆者の回答
// input関数定義部省略 (一番最初の節を見てください)
use std::cell::RefCell;
use std::collections::{BTreeSet, HashSet};
use std::rc::{Rc, Weak};
struct Player {
id: usize,
next: RefCell<Weak<Player>>,
prev: RefCell<Weak<Player>>,
}
impl Player {
fn new(id: usize) -> Rc<Self> {
Rc::new(Self {
id,
next: RefCell::new(Weak::new()),
prev: RefCell::new(Weak::new()),
})
}
fn set_next(self: &Rc<Self>, next: Weak<Self>) {
*self.next.borrow_mut() = next;
}
fn get_next(self: &Rc<Self>) -> Option<Rc<Self>> {
self.next.borrow().upgrade()
}
fn set_prev(self: &Rc<Self>, prev: Weak<Self>) {
*self.prev.borrow_mut() = prev;
}
fn get_prev(self: &Rc<Self>) -> Option<Rc<Self>> {
self.prev.borrow().upgrade()
}
fn new_players(n: usize) -> Vec<Rc<Self>> {
assert!(n > 0);
let mut players = Vec::with_capacity(n);
let top = Self::new(0);
players.push(Rc::clone(&top));
let mut now = Rc::clone(&top);
for id in 1..n {
let next = Self::new(id);
next.set_prev(Rc::downgrade(&now));
players.push(Rc::clone(&next));
now.set_next(Rc::downgrade(&next));
now = next;
}
// 環状にする
now.set_next(Rc::downgrade(&top));
top.set_prev(Rc::downgrade(&now));
players
}
fn out(self: &Rc<Self>) -> Option<Rc<Self>> {
match (self.get_prev(), self.get_next()) {
(Some(prev), Some(next)) => {
prev.set_next(Rc::downgrade(&next));
next.set_prev(Rc::downgrade(&prev));
}
// 環状なので上記以外の状況はない
_ => (),
}
self.get_prev()
}
fn count(self: &Rc<Self>) -> usize {
let mut count = 1;
let mut now = Rc::clone(self);
let top_id = now.id;
while let Some(player) = now.get_next() {
if player.id == top_id {
// 一周した
break;
}
count += 1;
now = player;
}
count
}
}
fn main() {
let mut stdin = BufReader::new(std::io::stdin());
let n_k_m: Vec<usize> = input_vec(&mut stdin).unwrap();
let n = n_k_m[0];
let k = n_k_m[1];
let m = n_k_m[2];
// 「3. 今までに発言された単語を発言してはならない。」を実現するためHashSetでremoveする
let mut word_list: HashSet<String> = (0..k)
.filter_map(|_| {
let word: String = input(&mut stdin).unwrap();
// 「4. z で終わる単語を発言してはならない。」があるので最初から除外する
if !word.ends_with("z") {
Some(word)
} else {
None
}
})
.collect();
let players = Player::new_players(n);
let mut current_player = Rc::clone(&players[0]);
for word in (0..m).map(|_| input::<_, String>(&mut stdin).unwrap()) {
if !word_list.remove(&word) {
current_player = current_player.out().unwrap();
}
current_player = current_player.get_next().unwrap();
}
// 残ったプレイヤー数
println!("{}", current_player.count());
// 番号が若い順に出力するため、一旦BTreeSetに蓄える
let mut player_ids = BTreeSet::new();
player_ids.insert(current_player.id + 1);
// プレイヤー数カウントと要領は同じ
let top_id = current_player.id;
while let Some(next_player) = current_player.get_next() {
if top_id == next_player.id {
break;
}
player_ids.insert(next_player.id + 1);
current_player = next_player;
}
for id in player_ids {
println!("{}", id);
}
}
しりとりで人が並んでいる様は「環状リスト」です!標準クレートで環状リストを便利に扱える機能はすぐに思い当たらず、paizaではサードパーティクレートは使えなかったので(ここまで言い訳)、結局 環状リストを自作 してしまいました...orz
struct Player {
id: usize,
next: RefCell<Weak<Player>>,
prev: RefCell<Weak<Player>>,
}
impl Player {
fn new(id: usize) -> Rc<Self> {...}
// ゲッターやセッター省略
/// 環状リストになっているプレイヤーたちの配列を返す
fn new_players(n: usize) -> Vec<Rc<Self>> {...}
/// しりとりでアウトになった時自身を環状リストから外す
fn out(self: &Rc<Self>) -> Option<Rc<Self>> {...}
/// 環状リストの要素数
/// 一周するまでで人数を判断
fn count(self: &Rc<Self>) -> usize {...}
}
next と prev フィールドが他のプレイヤーへの"弱"参照になっています!弱参照 std::rc::Weak はメモリリーク防止のために使用する参照カウンタ( Rc )の一種です。
ここに別なプレイヤーへの参照を与え、最初と最後の人もつなげることによって環状リストとしました!
今回は亜種を使用しましたが、こういったリスト構造を作りたい時は std::rc::Rc や std::cell::RefCell の出番です!参照カウンタ Rc によって所有権問題を解決した参照を提供でき、 RefCell によって内部可変性を持った不変参照を提供できます。
イキリポイント⑧
所有拳最終奥義!!!
-
Rc<RefCell<T>>!! -
Arc<Mutex<T>>!!
使えるシーンに出会えると嬉しい...
環状リストをモデリングできたおかげで main 関数は比較的読みやすくなっていると思います!
fn main() {
// 入力部
let mut stdin = BufReader::new(std::io::stdin());
let n_k_m: Vec<usize> = input_vec(&mut stdin).unwrap();
let n = n_k_m[0];
let k = n_k_m[1];
let m = n_k_m[2];
// 「3. 今までに発言された単語を発言してはならない。」を実現するためHashSetでremoveする
let mut word_list: HashSet<String> = (0..k)
.filter_map(|_| {
let word: String = input(&mut stdin).unwrap();
// 「4. z で終わる単語を発言してはならない。」があるので最初から除外する
if !word.ends_with("z") {
Some(word)
} else {
None
}
})
.collect();
// しりとりプレイ
// 環状リストを作成
let players = Player::new_players(n);
// 先頭プレイヤーを現在のプレイヤーにセット。ゲームスタート、といったところ
let mut current_player = Rc::clone(&players[0]);
// 単語を読み込んでいく
for word in (0..m).map(|_| input::<_, String>(&mut stdin).unwrap()) {
if !word_list.remove(&word) {
// ワードリストに存在しない単語を言ったらアウト
// (既に言われた単語や末尾がzの単語は除かれていっている)
current_player = current_player.out().unwrap();
}
// 次のプレイヤーへ
current_player = current_player.get_next().unwrap();
}
// 出力部
// 残ったプレイヤー数
println!("{}", current_player.count());
// 番号が若い順に出力するため、一旦BTreeSetに蓄える
let mut player_ids = BTreeSet::new();
player_ids.insert(current_player.id + 1);
// プレイヤー数カウントと要領は同じ
let top_id = current_player.id;
while let Some(next_player) = current_player.get_next() {
if top_id == next_player.id {
break;
}
player_ids.insert(next_player.id + 1);
current_player = next_player;
}
for id in player_ids {
println!("{}", id);
}
}
入力部や出力部を除けば、ほぼしりとりのワークフローを書き起こした感じになっており読みやすくなっていると思います!時間をかけて環状リストを用意した甲斐があった...いやダメだろ[]
まとめ・所感2
競プロ問題を題材に競プロ向きではないテクニックを紹介してきました。綺麗なソースコードだとアルゴリズムも読みやすくなるので、おそらく全く無駄ということはないですが、実戦向きのテクニックはそんなになかったんじゃないかと思います ![]()
こんな感じで競プロの問題を解いていると、Rustの機能・構文たちが魅力的すぎていつしか「いかに美しいアルゴリズムで解くか」よりも「いかに美しくプログラムを書くか」の方を気にしてしまうようになりました...読者の皆さんもぜひ競プロでRustに触れて、Rustの面白テクニック沼におぼれていってほしいです! ![]()
ここまで読んでいただきありがとうございました!