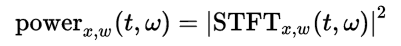numpyでスペクトログラムによる音楽信号の可視化

この記事はeeic Advent Calendar 2016 9日目の記事 その1 です。

去年はコード進行に関する記事を書かせてもらったのですが、あんまり情報系っぽくないですし、

【eeic向けアンケート】eeicｱﾎﾞﾍﾞﾝﾄﾞｶﾚﾝﾀﾞｰの記事を考えてるんですが、どっちの方がいいか意見聞きたいです

— なまおじ (@namaozi) 2016年11月8日

アンケートでは音楽プログラムの話の方が優勢だったので今回は音楽情報処理の話題で書きます。

この記事でやりたいこと

• スペクトログラムをpythonで実装してみる話
  • 数学・プログラミング分からない人でも読めるようにしたい
  • できるだけ定性的で音楽的な話を入れたい
• eeicと音楽情報処理について
  • 内輪向けなので興味ない方は飛ばしてください＞＜

実は上記の実装は神ライブラリを使えば3行くらいで書けてしまうのですが、せっかくなので極力高度なライブラリの使用は避けて、できるだけ実装の解説をしたいと思います。

ちなみにその2では、クロマグラムを使った和音認識にチャレンジします(こっちでは高度なライブラリ使います)。

おことわり

本記事はコレとかアレとか、並み居る神記事の劣化版です。ご了承ください。単純に実装をコピペするなら上述のリンクの方がオススメです。
本記事の新規性としては、ダウンロード可能な具体的な音源でいろいろやっている点と、次の記事でコード認識の応用までやっている点になるでしょうか。

まずはスペクトログラムから！

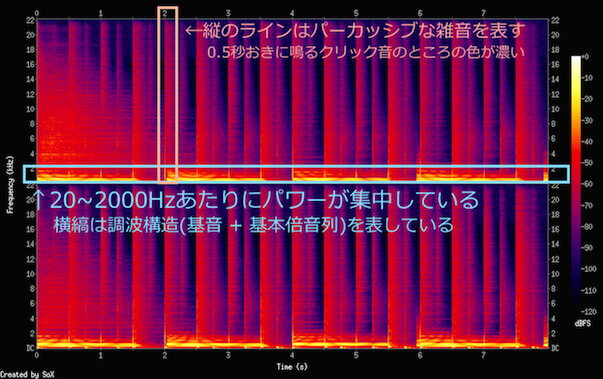
まずはスペクトログラムから実装していきます。スペクトログラム(spectrogram)は横軸に時間、縦軸に周波数をとった音楽の帯域の地図で、各点の色で信号の強さを表しています。

なお、この記事では全ての実装はpython2.7系で行います。本当に申し訳ございません。

コードはgithubに公開しましたので、そちらを見ながら試してみていただけたらと思います。

スペクトログラムを観察する

実はSoXというソフトウェアを使えばコマンドライン1行でスペクトログラムが作れるので、まずはそちらを試してみましょう。
githubからクローンしたディレクトリから以下のコマンドを実行すると、
用意したサンプル音源「harmony1.wav」の冒頭8秒間のスペクトログラムが得られます。

 sox ./audios/harmony1.wav -n trim 0 8 rate 44.1k spectrogram

このサンプル音源はBPM120でクリック音・8ビートドラム・オルガンのコードを入れた単純な音源です(LogicというDAWで作成しています)。
スペクトログラムは上下2つに分かれていますが、これはwavがステレオ音源でチャネルが2つあるからですね。

縦縞はパーカッシブ要素でして、和音認識をする上では雑音にしかならない要素です。「harmony1.wav」ではクリック音とドラムがこの縦縞の元になっています。
ファミコン音源などを扱ったことがある方は、ノイズの波形を見たことがあるでしょうか。周期が長く不規則な信号はこのように縦縞、つまりいろんな周波数成分を含んでいます。

縦軸が22kHzまでなのは、この音源がCDでの一般的なサンプリングレート(標本化周波数)である44.1kHzを採用しているからです。標本化定理により、サンプリングレートの半分 = 22.05kHz以下の周波数の原信号が完全再現可能になります。人間の可聴域が20~20,000Hzくらいなので、サンプリングレートは40kHzくらいで充分なのですね。ちなみに高級なオーディオインターフェースは192kHzくらいで録音できたりしますが、意味はあるんでしょうかね…(´･_･｀)

一番強いパワーが集中しているのは2kHzよりも下のあたりです。特に0付近が強いパワーを持っていますが、これはだいたいドラムのバスドラのせいですね。これがうるさいとか和音解析どころではなくなってしまいます。

(楽器の周波数帯について知りたい方はこちら)

もっと音楽的にスペクトログラムを知りたい！という方には、聴くだけ音感入門という本がオススメです。倍音と音色の関係とかが分かるようになると思います。

短時間フーリエ変換(STFT)

さて、数理的な話をします(飛ばしてもいいです)。観測した信号にどの周波数がどれくらい含まれているのかを調べるには、フーリエ変換が必要になります。しかしこのフーリエ変換は周期信号を仮定しているので、時々刻々と変化する音楽などの信号には不適です。そうした場合に用いるのが短時間フーリエ変換(STFT)です。

短時間フーリエ変換では信号に対して窓関数を徐々にずらしながらかけてフレームに分けていき、各フレームごとに周波数成分を求めるという方法です。

ちなみに高速フーリエ変換(FFT)は計算するアルゴリズムの名前です。

あと離散フーリエ変換(DFT)というのがあって、短時間フーリエ変換の違いはかなり説明が難しいのですが、とりあえず短時間フーリエ変換はスペクトログラムのような解析に使えると考えればいいと思います(筆者もあまりよく分かっていない…)。

短時間フーリエ変換は以下の画像が一番分かりやすいと思うので、こちらから引用しました。

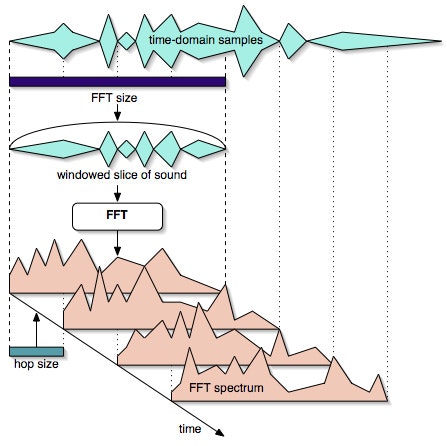
1. まず、元の信号をFFT sizeのフレームに分けていきます。(画像の一番上)

2. この際に窓関数をかけるのが重要で、これによって切り出した端点をなめらかにして周期性を仮定します。(画像のwindowed slice of soundというやつ)

3. これにFFT計算をすることによって各フレームの周波数成分が得られます。(画像の赤い波)

4. 短時間フーリエ変換のWikiに書いてあるとおり、STFTの絶対値の2乗をすることでスペクトログラム(パワースペクトルの時間変化)を得ます。

5. 次々に窓をずらしてフレームに分けていくことによって、時間ごとの周波数成分を求めていきます。(画像の点線に対応する赤い波)

では実際のプログラムで見てみましょう。

spectrogram.py

#coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
import scikits.audiolab as al
#⚠ wave読み込みにはscikits.audiolab.wavreadがオススメです。
#私はwaveというパッケージを先に試しましたが,wave.readframesの挙動がおかしかったので使用をやめました。

import functions as fn

"""
スペクトログラムを計算してプロットします
"""
### 楽曲データ読み込み(scikits.audiolab使用)
# data : ここにwavデータがnumpy.ndarrayとして保持されます。
# sampling_rate : 大半のwav音源のサンプリングレートは44.1kHzです
# fmt : フォーマットはだいたいPCMでしょう
file_path = "audios/harmony1.wav"
data, sampling_rate, fmt = al.wavread(file_path)

# ステレオファイルをモノラル化します
x = fn.monauralize(data)

NFFT = 1024 # フレームの大きさ
OVERLAP = NFFT / 2 # 窓をずらした時のフレームの重なり具合. half shiftが一般的らしい
frame_length = data.shape[0] # wavファイルの全フレーム数
time_song = float(frame_length) / sampling_rate  # 波形長さ(秒)
time_unit = 1 / float(sampling_rate) # 1サンプルの長さ(秒)

# 💥 1.
# FFTのフレームの時間を決めていきます
# time_rulerに各フレームの中心時間が入っています
start = (NFFT / 2) * time_unit
stop = time_song
step =  (NFFT - OVERLAP) * time_unit
time_ruler = np.arange(start, stop, step)

# 💥 2.
# 窓関数は周波数解像度が高いハミング窓を用います
window = np.hamming(NFFT)

spec = np.zeros([len(time_ruler), 1 + (NFFT / 2)]) #転置状態で定義初期化
pos = 0

for fft_index in range(len(time_ruler)):
    # 💥 1.フレームの切り出します
    frame = x[pos:pos+NFFT]
    # フレームが信号から切り出せない時はアウトです
    if len(frame) == NFFT:
        # 💥 2.窓関数をかけます
        windowed = window * frame
        # 💥 3.FFTして周波数成分を求めます
        # rfftだと非負の周波数のみが得られます
        fft_result = np.fft.rfft(windowed)
        # 💥 4.周波数には虚数成分を含むので絶対値をabsで求めてから2乗します
        # グラフで見やすくするために対数をとります
        fft_data = np.log(np.abs(fft_result) ** 2)
        # fft_data = np.log(np.abs(fft_result))
        # fft_data = np.abs(fft_result) ** 2
        # fft_data = np.abs(fft_result)
        # これで求められました。あとはspecに格納するだけです
        for i in range(len(spec[fft_index])):
            spec[fft_index][-i-1] = fft_data[i]

        # 💥 4. 窓をずらして次のフレームへ
        pos += (NFFT - OVERLAP)

### プロットします
# matplotlib.imshowではextentを指定して軸を決められます。aspect="auto"で適切なサイズ比になります
plt.imshow(spec.T, extent=[0, time_song, 0, sampling_rate/2], aspect="auto")
plt.xlabel("time[s]")
plt.ylabel("frequency[Hz]")
plt.colorbar()
plt.show()

上のプログラムを実行した結果が下の図です。

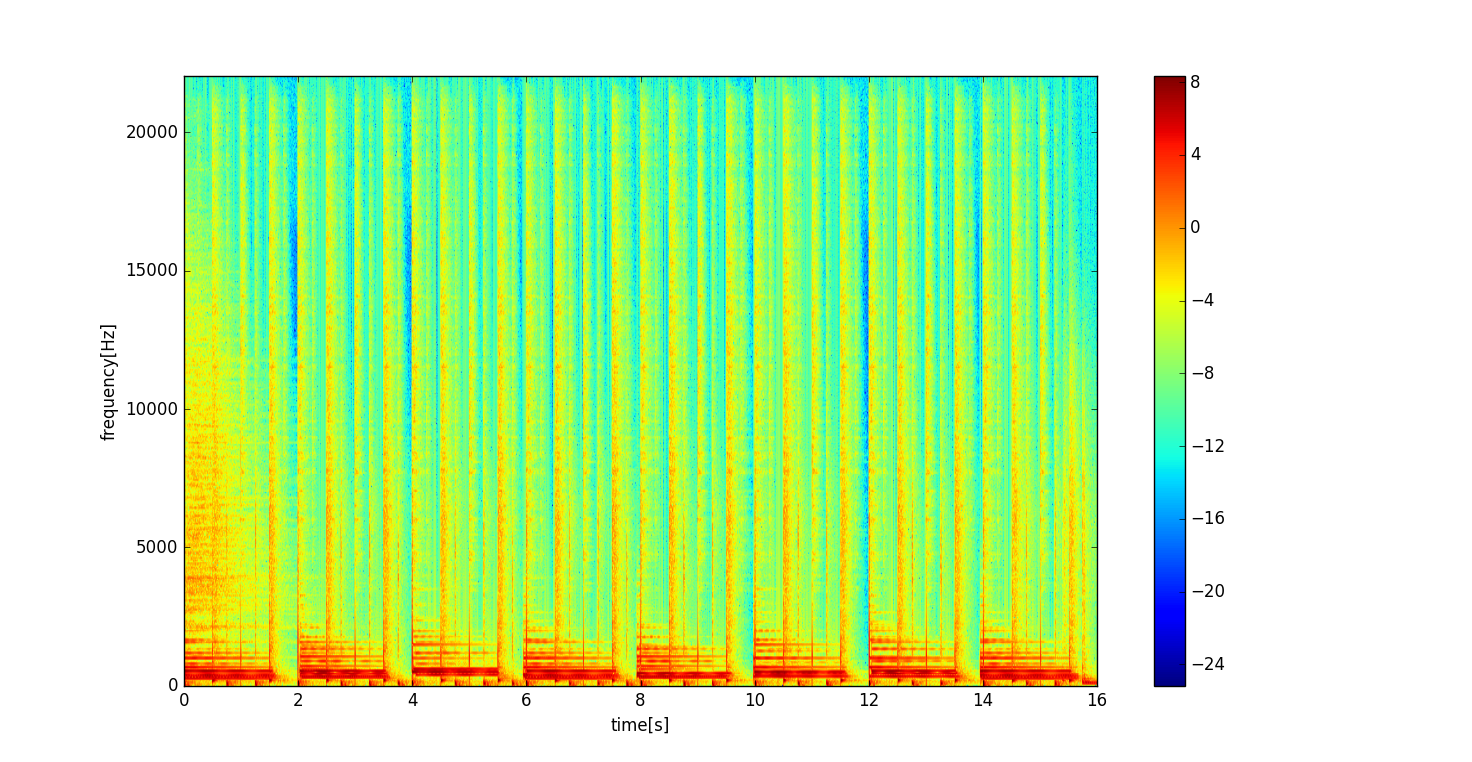
なんとなく調波構造とパーカッシブ成分が見えていますね。なおこちらのスペクトログラムは16秒分と、さっきのスペクトログラムの2倍の長さがあります。

ちなみに色はパワーに対応していますが、俗に音圧に対して言う"デシベル[dB SPL]"ではありませんのでご注意ください。曲全体における周波数成分の分布を表すための信号の強さの図、というふうに捉えていただけたらと思います。

いかがだったでしょうか。次の記事ではいよいよ和音認識にチャレンジしていきましょう。

おまけ：eeicと音楽情報処理

以下は内輪向けのおまけです。

残念ながらeeicでは音楽情報処理を学べません。(´･_･｀)

音楽情報処理は、音楽音響信号を数理的に解析して色々な情報を得る分野です。

例えば、今回扱う和音認識(chord estimation)をはじめとして、音源分離(source separation)、音高推定(pitch estimation)などのタスクなどがあります。

さらに、抽出した音楽情報をどのようにアプリケーションに活かすのか探求したり、またはリスナーの嗜好などの楽曲のメタ情報を用いて楽曲推薦をしたりなんかも音楽情報処理の領域です。楽しそうですよね！？？！！？！？

eeicではmnmt研が音声系の研究室として知られていますが、基本的に扱っているのは音声なので、音声・言語処理の分野になり、音楽情報処理とは異なる分野になります。

僕は音楽に執着㋔㋟㋗なので音楽信号解析とか扱う授業があったらなぁ〜とずっと思っていたのですが、学部の時にフーリエ変換を主とした信号処理については学べたものの、音楽に着目した応用的な授業はなかったのでとても残念に思っていました…(´･_･｀)

僕は訳あって今は音楽情報処理の研究をしているので、皆様にも少し紹介したいなと思ってこの記事を書きました。

今回はさわりの部分だけを紹介しますが、ある程度まともに音楽情報処理を勉強したい方には京大の実験のテキストをやってみることをオススメします！あとは序盤に紹介したリンクの神ブログがオススメです！