@namaoziです。
この記事はeeic Advent Calendar 2016 9日目の記事 その2 です。
いきなり その2 から見始めた方はよろしければ その1 を先にお読みください。
前回はスペクトログラムを作って音楽信号を可視化しました。
今回はクロマグラムを用いて
の和音認識にチャレンジしてみましょう。
この記事でやりたいこと
- クロマグラムを使って和音認識してみる
- なるべく数学・プログラミング分からない人でも読めるようにしたい
- できるだけ定性的で音楽的な話を入れていきたい
おことわり
ライブラリ、使います。
その1ではスペクトログラムをnumpyだけを使って実装したのですが、クロマグラムの和音認識は自分の実装だと精度がゴミofゴミすぎたのでライブラリ様に頼ることにします 、情けない話だ…(´・_・`)
…というわけでこの記事では高度なpythonの音声信号解析ライブラリのlibrosaを使ってクロマグラムを取得し、和音認識してみましょう。実際にやってみたい方はまずリンクからlibrosaをインストールしてください。
python2.7を使ってます
大変申し訳ありませんがpython2.7をこのサンプルでは使ってます、、、じきに3.0対応したいと思います
言葉の問題
音楽用語とかいろいろ出てきますが、分からないところは基本スルーして大丈夫だと思います。興味のある方は、リンクを貼るようにしますのでそちらを参照ください。
とりあえずコードは和音で、名前がついた和音がコードということさえわかっていればOKです。
和音(コード)認識とは
コンピューターにコード進行を耳コピさせるタスクです。
実は和音を推定するタスクは非常に難しい問題で、現在でも盛んに研究が続けられています。年々精度が改善されているものの、いまだに訓練された人間のように柔軟に和音を聴き分ける段階には至っていません。
詳しく知りたい方はこの辺の記事を読んでみてください。今回扱うクロマグラムのことも書かれています。最新手法についてはこちらのブログが詳しいです。
本当は隠れマルコフモデル(Hidden Markov Model, HMM)を用いた実装が主流なのですが、実装が大変なので今回は簡易版としてクロマグラムのみを用いてコード認識にチャレンジしたいと思います。
クロマグラムとは
クロマグラムは、全周波数帯域のパワーを[C, Db, D, Eb, E, F, Gb, G, Ab, A, Bb, B]の12音階に落とし込み、ある区間の時間における音の成分を可視化したものです。
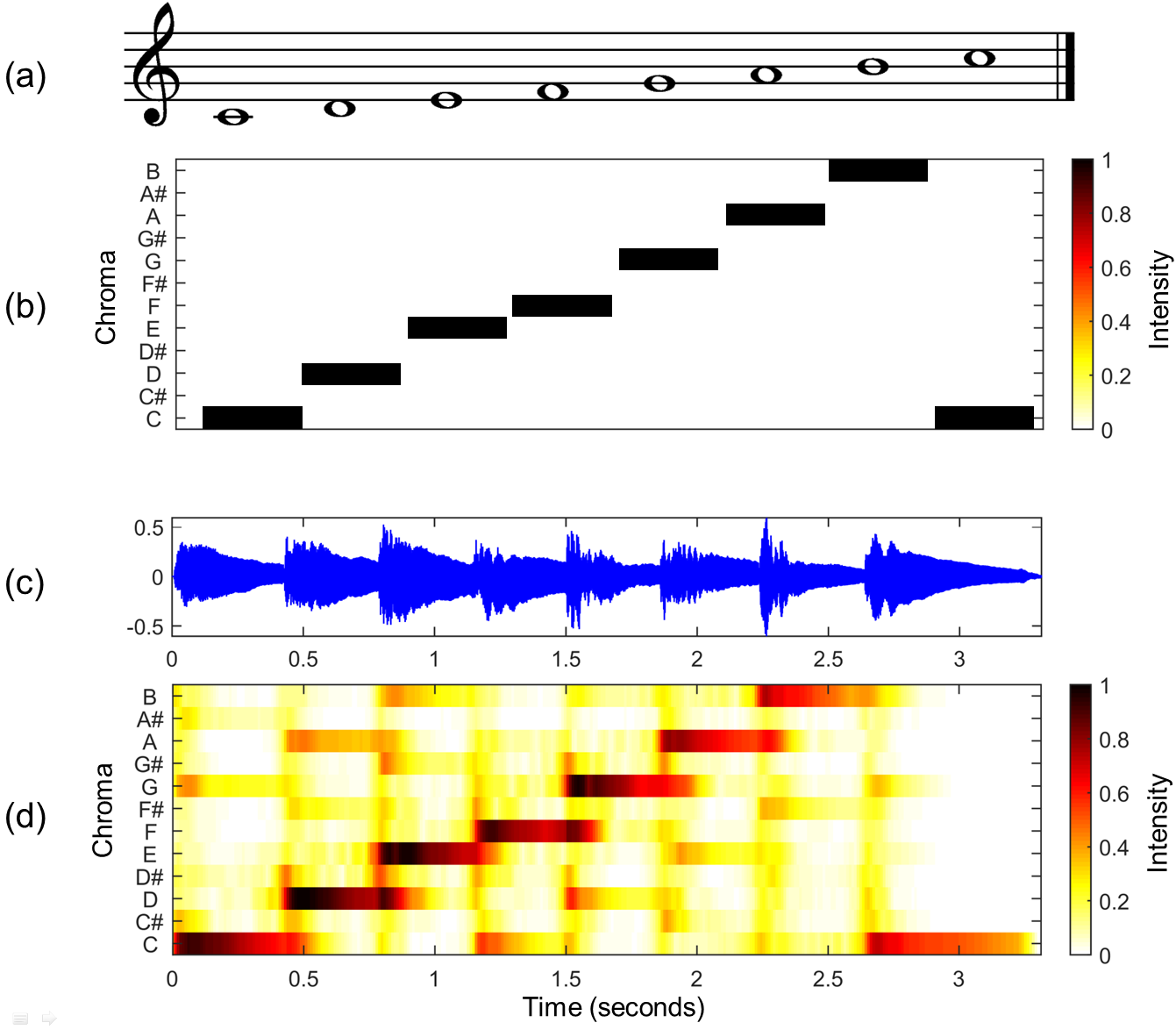
英語のwikiの画像で説明します。
(a)はCメジャースケール、いわゆるピアノの白鍵の音が並んでいる楽譜です。
(b)が(a)に対応する理論的なクロマベクトルになるんですが、実際にCメジャースケール(ハ長調)を弾いてみた音の波形である(c)からクロマグラムを作成すると(d)のようになります。
イメージとしては音楽信号をピアノロール1オクターブ分に全て押し込んだ感じでしょうか。
各時刻における信号は12音の成分の強さで表せるので、クロマベクトルと言ったりもします。
結局どうやるの?
どうやってコード認識するのかという話ですが、
"音楽信号のクロマグラムがどれくらい欲しいコードのクロマベクトルと似ているのか"
によって各時刻のコードを決めていきます。具体的には以下のような手順になります。
1. 認識したいコードのクロマベクトル(テンプレートベクトル)を作る
2. 楽曲のクロマグラムを作る
3. 各時刻のクロマグラムとテンプレートベクトルの類似度を計算して、最も類似度が高いコードをその時刻のコードと推定する
1.テンプレートベクトルを作る
まず、認識したいコード(和音)の理想的なクロマベクトルを作っておきます。以降ではこうした理想的なクロマベクトルをテンプレートベクトルと呼ぶことにします。
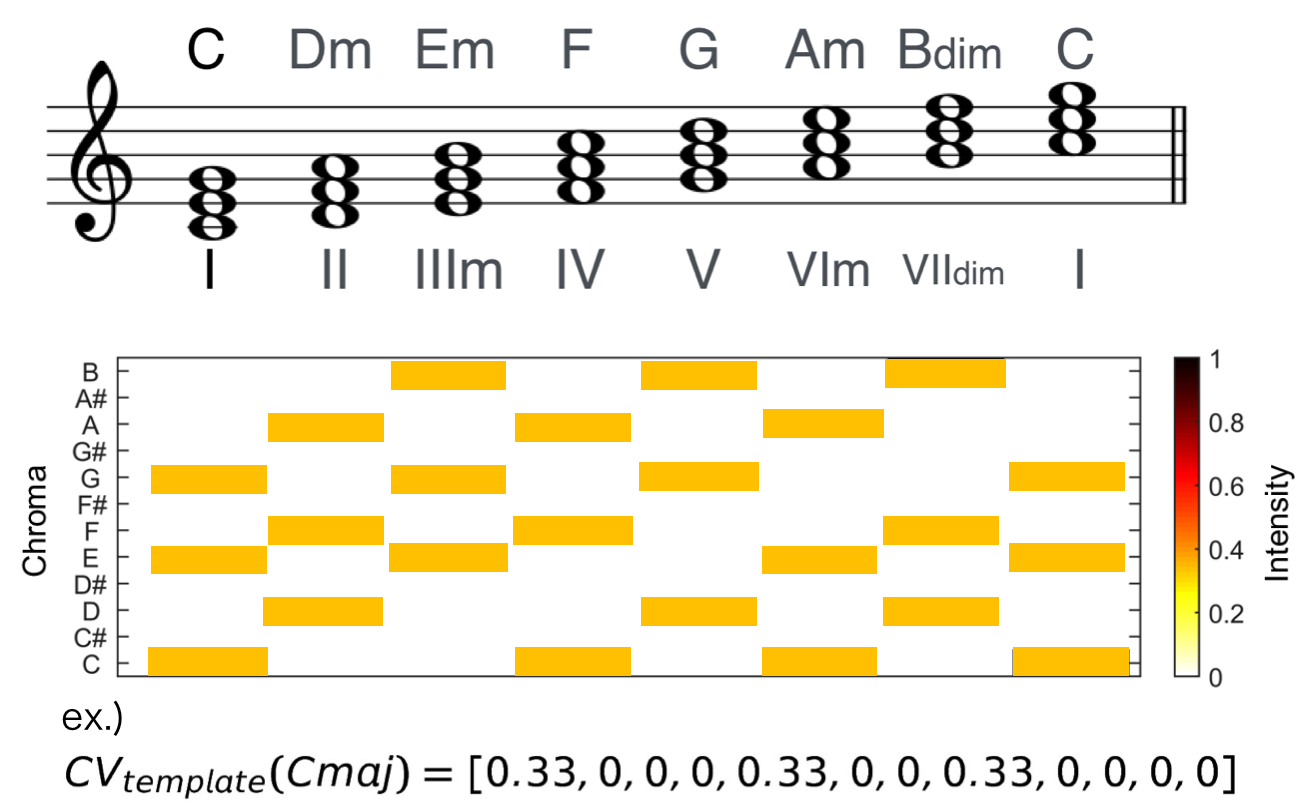
たとえばダイアトニックコードは下の図のような感じのテンプレートベクトルになりますね。ちなみにダイアトニックコードというのは、ある調の構成音を3度ずつ、つまり1つ飛ばしで堆積させた和音です(長調・短調それぞれにダイアトニックコードがありますが下の画像は長調です)。
ちなみにさっきは黒かったのに上の画像のクロマベクトルの色が違っているのは、ある時刻における各ピッチクラスのパワーの和を1にそろえるためです。
上の画像の一番下に書いてある数式がCメジャーコードのテンプレートベクトルを数式で表したものになります。各次元が12種類のピッチクラスに対応していて、Cから順に半音ずつ上がっています。
2.クロマグラムを作る
先ほど紹介したクロマグラムを作ります。神ライブラリのlibrosa様に頼りましょう。ついでなのでパーカッシブ成分を分離したものを解析しています。内部で何をしているか気になる方は神ドキュメントを参照ください。
コードはGitHubに置いてありますのでよかったら試してみてください。
https://github.com/namaozi/ChromagramSample
def librosa_chroma(file_path="audios/harmony1.wav", sr=44100):
#インポート(インストールしないと使えません)
import librosa
# 読み込み(sr:サンプリングレート)
y, sr = librosa.load(file_path, sr=sr)
# 楽音成分とパーカッシブ成分に分けます
y_harmonic, y_percussive = librosa.effects.hpss(y)
# クロマグラムを計算します
C = librosa.feature.chroma_cens(y=y_harmonic, sr=sr)
# プロットします
plt.figure(figsize=(12,4))
librosa.display.specshow(C, sr=sr, x_axis='time', y_axis='chroma', vmin=0, vmax=1)
plt.title('Chromagram')
plt.colorbar()
plt.tight_layout()
plt.show()
return C
###
なんと数行でクロマグラムが計算できちゃいます。はぁライブラリ神…
以下が得られたクロマグラムです。
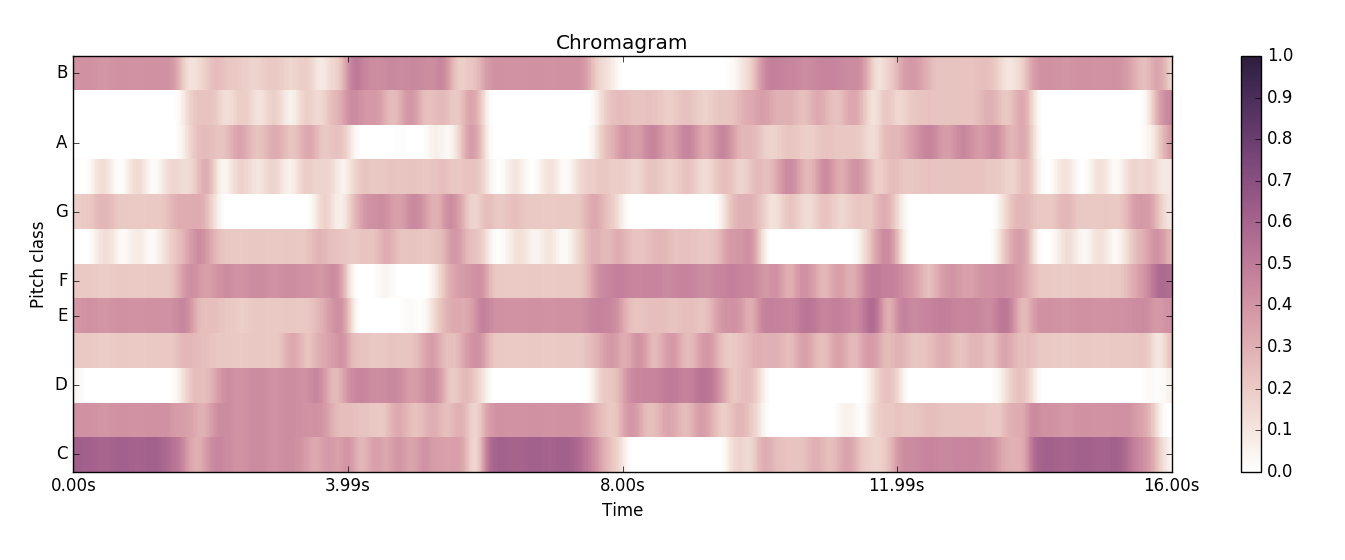
このサンプル音源はBPM120で
というコードを順に4拍ずつ、つまり2秒ずつ伸ばしています。得られたクロマグラムを見ると、2秒ごとのコードチェンジのタイミングで色の濃淡が変わり、信号の音の成分が変わっているのが分かるかと思います。 1
更に、例えば3つめ、4秒~6秒の間のGメジャーコードのクロマグラムはD, G, Bの部分の色が濃くなっていて、これはGメジャーコードの構成音と一致しています。クロマグラムを見るだけでなんとなくコードが分かりそうですよね! 2
3. コード推定
あとは時間軸に沿ってコードを推定していくだけです。
# coding:utf-8
from collections import OrderedDict
import numpy as np
import matplotlib.pyplot as plt
import librosa #インストールしてください!
import soundanalysis as sa
file_path = "audios/"
file_name = "harmony1.wav"
# クロマグラムを求めます
chroma = sa.librosa_chroma(file_path + file_name)
TONES = 12 # ピッチクラス,音の種類の数
sampling_rate = 44100 #音源依存
# "この設定では",こんな感じで時間軸設定を求められます
# (詳しくはドキュメントを読んで下さい)
time_unit = 512.0 / 44100 # 1フレームのクロマグラムの長さ
# stop = time_unit * (chroma.shape[1] - 1)
stop = time_unit * (chroma.shape[1])
time_ruler = np.arange(0, stop, time_unit)
### コードのテンプレートベクトルです
# メジャーとマイナーだけを考えます
# 脳筋コード,時間が無かったので…
# 順番を保ちたいのでOrderdDictを使います
one_third = 1.0/3
chord_dic = OrderedDict()
chord_dic["C"] = [one_third, 0,0,0, one_third, 0,0, one_third, 0,0,0,0]
chord_dic["Db"] = [0, one_third, 0,0,0, one_third, 0,0, one_third, 0,0,0]
chord_dic["D"] = [0,0, one_third, 0,0,0, one_third, 0,0, one_third, 0,0]
chord_dic["Eb"] = [0,0,0, one_third, 0,0,0, one_third, 0,0, one_third, 0]
chord_dic["E"] = [0,0,0,0, one_third, 0,0,0, one_third, 0,0, one_third]
chord_dic["F"] = [one_third, 0,0,0,0, one_third, 0,0,0, one_third, 0,0]
chord_dic["Gb"] = [0, one_third, 0,0,0,0, one_third, 0,0,0, one_third, 0]
chord_dic["G"] = [0,0, one_third, 0,0,0,0, one_third, 0,0,0, one_third]
chord_dic["Ab"] = [one_third, 0,0, one_third, 0,0,0,0, one_third, 0,0,0]
chord_dic["A"] = [0, one_third, 0,0, one_third, 0,0,0,0, one_third, 0,0]
chord_dic["Bb"] = [0,0, one_third, 0,0, one_third, 0,0,0,0, one_third, 0]
chord_dic["B"] = [0,0,0, one_third, 0,0, one_third, 0,0,0,0, one_third]
chord_dic["Cm"] = [one_third, 0,0, one_third, 0,0,0, one_third, 0,0,0,0]
chord_dic["Dbm"] = [0, one_third, 0,0, one_third, 0,0,0, one_third, 0,0,0]
chord_dic["Dm"] = [0,0, one_third, 0,0, one_third, 0,0,0, one_third, 0,0]
chord_dic["Ebm"] = [0,0,0, one_third, 0,0, one_third, 0,0,0, one_third, 0]
chord_dic["Em"] = [0,0,0,0, one_third, 0,0, one_third, 0,0,0, one_third]
chord_dic["Fm"] = [one_third, 0,0,0,0, one_third, 0,0, one_third, 0,0,0]
chord_dic["Gbm"] = [0, one_third, 0,0,0,0, one_third, 0,0, one_third, 0,0]
chord_dic["Gm"] = [0,0, one_third, 0,0,0,0, one_third, 0,0, one_third, 0]
chord_dic["Abm"] = [0,0,0, one_third, 0,0,0,0, one_third, 0,0, one_third]
chord_dic["Am"] = [one_third, 0,0,0, one_third, 0,0,0,0, one_third, 0,0]
chord_dic["Bbm"] = [0, one_third, 0,0,0, one_third, 0,0,0,0, one_third, 0]
chord_dic["Bm"] = [0,0, one_third, 0,0,0, one_third, 0,0,0,0, one_third]
prev_chord = 0
sum_chroma = np.zeros(TONES)
estimate_chords = []
result = np.zeros((TONES * 2, 8))
for time_index, time in enumerate(time_ruler):
# 今は何番目のコードを解析しているのか
# 2秒おきに変わるので2で割って求めます
nth_chord = int(time) / 2
# 次の2秒間に移る時に,前の2秒間のコードを推定します
if nth_chord != prev_chord:
maximum = -100000
this_chord = ""
# コサイン類似度が最大になるコードを調べます
for chord_index, (name, vector) in enumerate(chord_dic.iteritems()):
similarity = sa.cos_sim(sum_chroma, vector)
result[chord_index][nth_chord - 1] = similarity
if similarity > maximum:
maximum = similarity
this_chord = name
# 初期化、推定したコードを格納します
sum_chroma = np.zeros(TONES)
estimate_chords.append(this_chord)
else:
# chromaのshapeに注意しながら足していきます
for i in range(TONES):
sum_chroma[i] += chroma[i][time_index]
# 更新
prev_chord = nth_chord
###
# 最終結果です
print estimate_chords
### がんばってプロットします
axis_x = np.arange(0, 16, 2)
bar_width = 0.07
colors = ["#ff9999", "#ffaf95","#fabb92","#ffd698","#fae991","#c1fc97","#97fac8","#96f9f5","#98e1fb","#9cb2ff","#b79bfe","#fa96f9", "#b36a6a", "#ab7361","#aa7d61","#ad9165","#b4a765","#8ab66b","#6ab48f","#68b0ad","#689fb3","#6979b0","#7462a3","#aa62a9"]
for i, (name, vector) in enumerate(chord_dic.iteritems()):
plt.bar(axis_x - ((axis_x[1] - axis_x[0]) * 0.45) + bar_width * i, result[i], color=colors[i], width = bar_width, label = name, align = "center")
plt.legend()
plt.xticks(axis_x + bar_width / 24)
plt.show()
というコード列が得られました!!
入力した曲のコードは
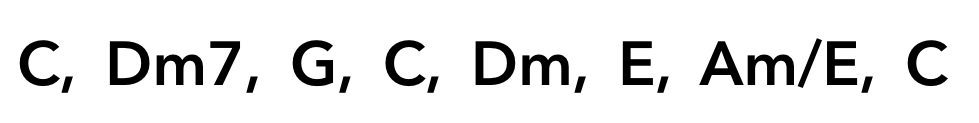
だったのですが、今回はメジャーとマイナーコードしか認識できないので、2つめのDm7(Dマイナーセブンス)はそもそも正解が出力できません。Dm7の構成音が[D,F,A,C]であることを考えると,DマイナーかFメジャーであればそれなりに認識出来ていることになります。出力ではFメジャーが得られているのでほぼ正解ですね。
7つめのコードAm/Eも、構成音はAmと同じなので出力のAmで正解です。
こうしてみると、サンプル音源「harmony1.wav」では、クロマグラムとテンプレートベクトルを使って、全てのコードに対してほぼ正解を出力することが出来ました!めでたしめでたし。 3
各区間の全コードに対する類似度をプロットしたものが以下の図になります(上のプログラムを実行すれば得られます)、とてもきれいな可視化ではないですが、、、
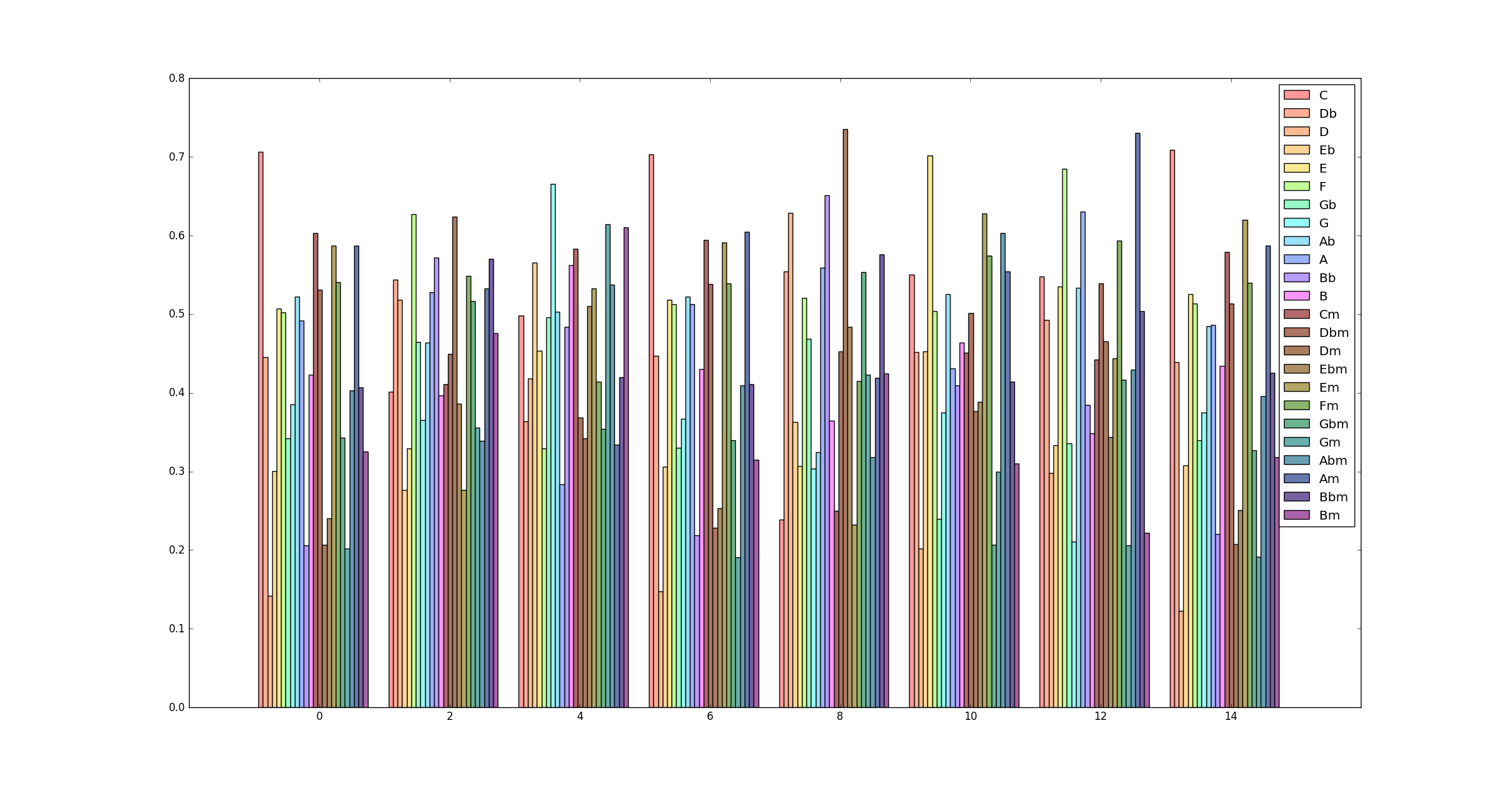
この図を(がんばって)見ると、例えば最初の0~2秒の区間ではCの類似度が一番高くなっていますが、そのほかに同主単調の主和音のCm, 平行調の主和音のAm, 属調(IIIm)の主和音Emなどでも類似度が高くなっていることがわかると思います。
このように関係調の主和音の類似度が似通っていることが分かると思います。このような数理的解釈から音楽理論を再考してみるのも面白いかもしれませんね。
まとめ
- pythonはべんり
- librosa最強
- 自分で実装する前にライブラリでできないか探しましょう
- コード認識は最強のライブラリを使っても結構難しい
-
本当はどこからどの区間までがそのコードであるのかも計算で決めなければいけないのですが、今回のサンプル音源では2秒おきにコードが変わっていますので、その情報をプログラムに与えてしまいます。 ↩
-
興味がある方は、audiosフォルダにいくつかサンプル音源を入れていますのでそちらを聴いてみて、クロマグラムを作ってみると面白いかもしれません。harmony1.wavがオルガンのコードとドラムだけだったのに対し、harmony2.wavはベースを加え、harmony3.wavが更にメロディーを加えた音源になっています。実際にクロマグラムを見ると、メロディーやベースの音に対応する部分の色が濃くなって見えるはずです。 ↩
-
実世界の曲は、単純なクロマグラムだけからこんなにうまく耳コピができちゃうことは残念ながらまずありません。harmony1.wavは和音+ドラムのみというごく単純な構成でしたが、実世界の曲は無限のトラック数を使った複雑な曲が多いです。それに歌声のメロディーなんかが入ると大きく影響を受けるので、和音を推定することは更に難しくなります。脚注1で述べた、「どの区間がそのコードであるのか」を推定するのも難しいので、余計に和音解析タスクが難しくなります。 ↩