はじめに
Pythonと強化学習の勉強を兼ねて,ブラックジャックの戦略作りをやってみました.
ベーシックストラテジーという確率に基づいた戦略がありますが,それに追いつけるか試してみます.
こんな感じで進めていきます
- ブラックジャック実装
- OpenAI gymの環境に登録
- 強化学習でブラックジャックの戦略を学習 ← 今回はここ
開発環境
- Windows 10
- Python 3.6.9
- Anaconda 4.3.0 (64-bit)
- gym 0.15.4
強化学習をコーディング
今回は,基本的な強化学習のアルゴリズムの一つであるQ-Learningを使います.
ファイル構成
ファイル構成は以下のようにします.
今回作成する強化学習のコードは「q-learning_blackjack.py」です.
その他のファイルは「OpenAI gymの環境に登録」のように作成しています.
├─ q-learning_blackjack.py
└─ myenv
├─ __init__.py ---> BlacJackEnvを呼び出す
└─env
├─ __init__.py ---> BlackJackEnvのある場所を示す
├─ blackjack.py ---> BlacJackのゲーム自体
└─ blackjack_env.py ---> OpenAI Gymのgym.Envを継承したBlackJackEnvクラスを作る
コーディング
Agentクラス
self.QがQ値をまとめたテーブルとなり,学習の進行にともなって更新します.これをここではQテーブルと呼びます.
Qテーブルは,状態(Playerのポイント,Dealerのポイント,PlayerがAceを保有しているか,PlayerがHit済みか)に対して,PlayerがStand,Hit,Double Down,Surrenderという行動をとったときの価値を表します.
policyメソッドはε-greedy法に従って行動を選択します.
確率epsilonでランダムに行動を選択し,確率1-epsilonでQテーブルに従って行動を選択します.
class Agent():
def __init__(self, epsilon):
self.Q = {}
self.epsilon = epsilon
self.reward_log = []
def policy(self, state, actions):
if np.random.random() < self.epsilon:
return np.random.randint(len(actions))
else:
if state in self.Q and sum(self.Q[state]) != 0:
return np.argmax(self.Q[state])
else:
return np.random.randint(len(actions))
def init_log(self):
self.reward_log = []
def log(self, reward):
self.reward_log.append(reward)
def show_reward_log(self, interval=100, episode=-1):
if episode > 0:
rewards = self.reward_log[-interval:]
mean = np.round(np.mean(rewards), 3)
std = np.round(np.std(rewards), 3)
print("At Episode {} average reward is {} (+/-{}).".format(episode, mean, std))
else:
indices = list(range(0, len(self.reward_log), interval))
means = []
stds = []
for i in indices:
rewards = self.reward_log[i:(i + interval)]
means.append(np.mean(rewards))
stds.append(np.std(rewards))
means = np.array(means)
stds = np.array(stds)
plt.figure()
plt.title("Reward History")
plt.xlabel("episode")
plt.ylabel("reward")
plt.grid()
plt.fill_between(indices, means - stds, means + stds, alpha=0.2, color="g")
plt.plot(indices, means, "o-", color="g", label="Rewards for each {} episode".format(interval))
plt.legend(loc="best")
plt.savefig("Reward_History.png")
plt.show()
QLearningAgentクラス
上記で作成したAgentクラスを継承します.
learnメソッドが学習のメインです.1エピソードがブラックジャックの勝負1回分に相当します.
a = self.policy(s, actions)で状態に応じて行動を選択し,n_state, reward, done, info = env.step(a)で実際にその行動をとった結果の状態と報酬を観測します.step関数は「OpenAI gymの環境に登録」で実装した通りです.
下記の3行のコードがQ-Learningの式
Q(s_t, a_t)\leftarrow(1-\alpha)Q(s_t, a_t)+\alpha(r_{t+1}+\gamma \max_{a_{t+1}}Q(s_{t+1}, a_{t+1}))
に相当します.
$\gamma$(gamma)は割引率で将来の価値をどれだけ割り引いて考えるかのパラメータ,$\alpha$(learning_rate)は学習率で,Q値の更新をどれだけ急激に行うか制御するパラメータです.
gain = reward + gamma * max(self.Q[n_state])
estimated = self.Q[s][a]
self.Q[s][a] += learning_rate * (gain - estimated)
class QLearningAgent(Agent):
def __init__(self, epsilon=0.1):
super().__init__(epsilon)
def learn(self, env, episode_count=1000, gamma=0.9,
learning_rate=0.1, render=False, report_interval=5000):
self.init_log()
actions = list(range(env.action_space.n))
self.Q = defaultdict(lambda: [0] * len(actions))
for e in range(episode_count):
s = env.reset()
done = False
reward_history = []
while not done:
if render:
env.render()
a = self.policy(s, actions)
n_state, reward, done, info = env.step(a)
reward_history.append(reward)
gain = reward + gamma * max(self.Q[n_state])
estimated = self.Q[s][a]
self.Q[s][a] += learning_rate * (gain - estimated)
s = n_state
else:
self.log(sum(reward_history))
if e != 0 and e % report_interval == 0:
self.show_reward_log(episode=e, interval=50)
env.close()
train関数
env = gym.make('BlackJack-v0')で自作したブラックジャック環境を読み込みます.
作成方法はブラックジャック実装 ,OpenAI gymの環境に登録を参照してください.
Q値のテーブルの保存用にsave_Qメソッド,報酬のログ履歴の表示用にshow_reward_logメソッドを作成しました.
def train():
agent = QLearningAgent()
env = gym.make('BlackJack-v0')
agent.learn(env, episode_count=50000, report_interval=1000)
agent.save_Q()
agent.show_reward_log(interval=500)
if __name__ == "__main__":
train()
学習結果
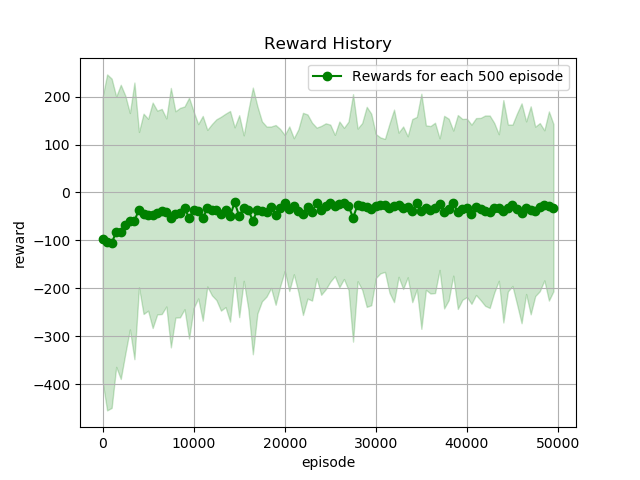
学習結果が以下の通りです.
横軸がエピソード,縦軸が報酬です.緑色の線が500エピソードの平均報酬,緑色の塗りつぶしが500エピソードの報酬の標準偏差です.
20000エピソード以降はほぼ横ばいです.そして50000エピソード学習時点でも平均報酬が0を下回っていることに悲しさを感じます...
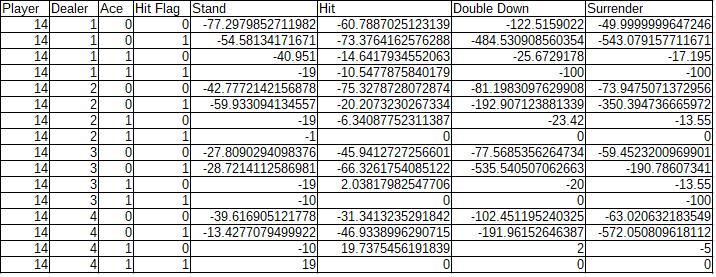
ベーシックストラテジーとの比較
学習したQテーブルをベーシックストラテジーと比較します.Qテーブルの各状態ごとにQ値が最大となる行動を抽出して,ベーシックストラテジーと同じように,ハードハンド,ソフトハンドごとに戦略の表を作ります.
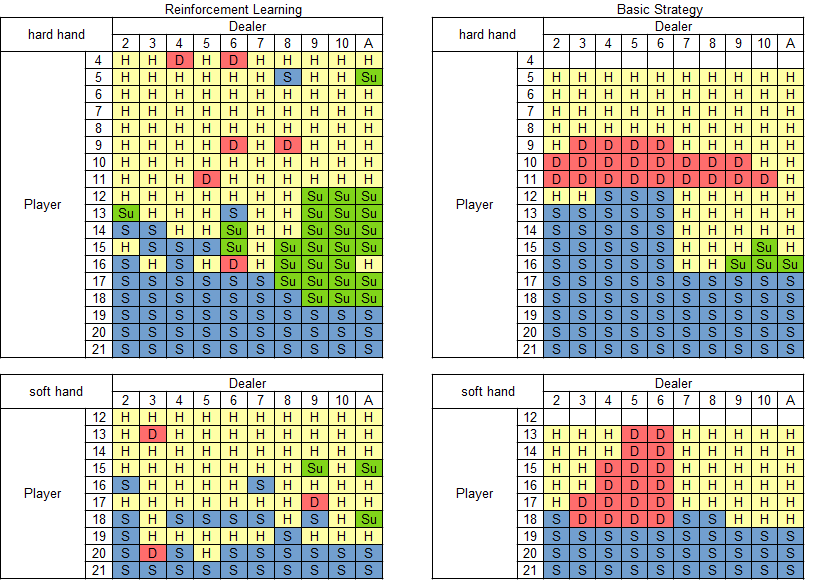
左列がQ-Learningで学習した戦略,右列がベーシックストラテジーです.
上段がハードハンド(手札にAを含まない場合),下段がソフトハンド(手札にAを含む場合)です.
各表の行はPlayerのポイント,列はDealerのポイントを表します.
表中のアルファベットはPlayerがとるべき行動を表します.
- H : Hit
- S : Stay
- D : Double Down
- Su : Surrender
なお今回の自作のブラックジャックにはスプリットの機能は実装しておりません.なので,ハードハンドのPlayerが4ポイント(2, 2)のとき,ソフトハンドのPlayerが12ポイント(A, A)のときにも行動が割り当てられています.
学習した結果をベーシックストラテジーと比べてみると,Playerのポイントが低いときはHit,高いときはStayという傾向は一致しています.このあたりは最低限学習してほしいところですね.ところが細かいところを見てみるとソフトハンドのPlayerが19ポイントではHitしがちです.たとえHitしてもBustすることはないのですが,黙ってStayしていれば強い手なんですよね.ここはうまく学習できなかったところです.なぜでしょうか...
またDouble Downが少なく,Surrenderが多い傾向です.リスクはとらず損は最小限にしようとする傾向がうかがえます.
実際にプレイさせてみた
学習したQテーブルに基づいたプレイとベーシックストラテジーに基づいたプレイを100ゲーム×1000回させてみました.
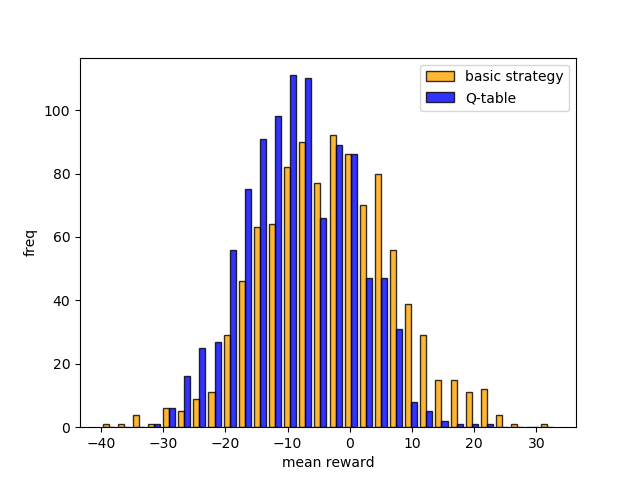
各ゲームでは$100を賭け,100ゲーム実施時の平均獲得チップを1000回算出しました.その平均獲得チップのヒストグラムが下図です.
図の右側に分布するほど良い成績であることを表しますが,ベーシックストラテジーの方が良い成績を出していますね.
ちなみにQテーブルに基づいた場合の平均値は$-8.2,ベーシックストラテジーに基づいた場合の平均値は$-3.2でした.
平均獲得チップが高いケースはもちろんベーシックストラテジーですが,低いケースもベーシックストラテジーでした.ベーシックストラテジーの方が分布が広いです.Qテーブルの方はDouble Downが少なくSurrenderが多いという傾向からか分布が狭くなっています.
おわりに
3つのステップを通して,自作のブラックジャック環境を作成し,戦略を強化学習させてみました.
結果的に,ベーシックストラテジーを超える結果は得られませんでしたが,自分の中で強化学習やプログラミングの理解を深めることができました.
学習の方はまだまだ改良の余地ありです.環境を自作しているので,残りの山札から出てくるカードの期待値も観測することができます.ちょっとズルにはなりますが実験してみたいと思います.(もちろんカジノでは使えないですが...)