この記事は「【リアルタイム電力予測】需要・価格・電源最適化ダッシュボード構築記」シリーズの十一日目です
Day1はこちら | 全体構成を見る
前回は、LightGBM単体で電力価格の予測を行いました。
その時の精度はこちらになります。
{'PICP(P10-P90)': 0.8525029967463896,
'MIW(P10-P90)': 6.129476481838045,
'IntervalScore_80': 8.272437129051259,
'Pinball_p10': 0.3832302375849058,
'Pinball_p50': 0.8451305145955873,
'Pinball_p90': 0.44401347532022,
'CRPS_approx': 0.5574580758335711}
今日はGAM(一般化加法モデル)を使ってLightGBM単体時の精度を上げられるように工夫してみます!
GAMとは
電力価格のように 複数の要因が非線形に影響し合うデータ を分析する際、どのモデルを使うかによって捉えられる構造が大きく変わります。
ここでは、線形回帰 → 一般化線形 → 加法モデル → 一般化加法モデル(GAM) の順番で、どのように表現力が高まっていくのかを整理していきます。
1. 線形回帰(Linear Regression)
もっとも基本的なモデルです。
例:「気温が1℃上がると電力需要が0.5万kW増える」といった 直線的な関係 を仮定します。
式は次のようになります。
$\text{demand} = \beta_0 + \beta_1 \cdot \text{temperature}$
しかし現実には、
- 気温が20℃を超えるとエアコン需要が急増する
- 寒すぎる日も暖房需要が増える(U字型)
このような 非線形の関係を直線で近似すると誤差が増える という問題があります。
2. 一般化線形モデル(GLM)
線形回帰の拡張で、目的変数の分布 を指定できるようにしたモデルです。
例えば、
- 需要 → 正規分布
- 発電量の故障回数 → ポアソン分布
- ある時間帯の価格が閾値を超えるか → ロジスティック回帰
$g(\mathbb{E}[y]) = \beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p$
など、データの特性に応じてリンク関数を選べるのが特徴です。ただし関係性は依然として 線形 のままです(リンク関数を通した平均が説明変数の線形結合になる)。
3. 加法モデル(Additive Model, AM)
「線形ではなく 曲線で近似したい」という場面で登場します。
例:気温と需要の関係を U 字型で表したい
$demand=β0+f1(temperature)$
この ${f_1}$ が「自由な形状を持てる曲線(スプライン)」です。
ただし AM は以下の場合が多いです
- 目的変数が正規分布前提
- 関係は加法のみ(掛け算のような相互作用なし)
4. 一般化加法モデル(GAM)
最後に登場するのが GAM(Generalized Additive Model) です。
これは GLM と AM のいいとこ取りです。
- 目的変数の分布 → 自由(厳密には、GLM と同様に指数型分布族+リンク関数の組み合わせから選びます)= GLMの良さ
- 説明変数との関係 → 曲線で柔軟に = AM の良さ
式で書くと:
$g(E[y])=β0+f1(x1)+f2(x2)+⋯+fp(xp)$
例:電力価格を説明する GAM
- $f_1(\text{temperature})$ → 気温が暑い/寒いほど価格が急上昇(非線形)
- $f_2(\text{solar})$ → 太陽光が多いほど価格低下(上に凸の曲線)
- $f_3(\text{demand})$ → 需要が一定ラインを超えると急騰(非線形)
このように、各要因の影響を「曲線」として直感的に理解できるのが GAM の最大の特徴です。
気温のU字型、太陽光の谷型、需要のS字型といった ゆるやかな形の非線形 が多い場合、GAMで表現できる可能性があります。
- 参考
方針
以下のように実験していきたいと思います。
- GAMで予測 + 残差をLightGBMで予測
- GAMで予測 + GAMの出力を特徴量の一つに加えてLightGBMで予測
ここでは、モデルが捉える構造が異なるので以下のように役割分担させようと思います。
- GAM:なめらかなカーブで説明したい 基礎構造 担当
- LightGBM:残ったゴツゴツした部分・相互作用・スパイク担当
GAMで学習
GAMモデルは以下のようにインストールしました。
from pygam import LinearGAM, s, f
GAMに入れる特徴量は以下のようにしました。
gam = LinearGAM(
# 需要・気温・日射・風速
s(0) + # demand
s(1) + # demand_7d_ma
s(2) + # temperature
s(3) + # temp_7d_ma
s(4) + # solar_radiation
s(5) + # wind_speed
# 時間(周期的)
s(6, basis="cp") + # hour
s(7, basis="cp") + # day_of_year
# カテゴリ
f(8) # is_holiday
)
LinearGAMは以下のような式をしています。この LinearGAM は「正規誤差・恒等リンクのGAM(一般化加法モデル)」を実装したクラスです。
$y=β0+f1(x1)+f2(x2)+⋯+fk(xk)+ε$
※LinearGAM は線形回帰という意味ではなく、GLM の線形予測子(additive linear predictor)を加法的に組み立てるGAMを指します。説明変数との関係はすべてスプラインで非線形に学習されます。(誤差:正規分布、リンク関数:恒等リンク、モデル:一般化加法モデルということ)
各${f_j}$をどう表現するかを s() や f() で決めています。
-
$s(j)$: 連続量用
- B スプラインや cubic スプラインの和として表現し、その係数を最尤推定+平滑化ペナルティで推定する
- 「x が小さいときは価格が下がるけど、真ん中あたりで底を打って、また上がる」といった非線形な一変量関数 を一気に学習できる
-
$f(j)$: カテゴリ用
- 列 j を「0/1/2/…」の整数ラベルとみなし、それを one-hot(ダミー変数)に展開して係数を推定する
- 「休日かどうかで平均値にどれくらい差があるか」「季節ごとにベースラインをずらす」のような段差のある効果 を表現する
-
basis= "cp"- "cp" = cyclic spline(周期的なスプライン)のことを指す
- 例えば。0 時と 23 時、1 日目と 365 日目が つながるように 制約をかける
⇒今回は周期性を入れたいので hour と day_of_year にだけ basis="cp" を使っています。
データ準備
X_gam_train = train_df[gam_features].copy() # GAM専用
X_gam_train["is_holiday"] = X_gam_train["is_holiday"].cat.codes.astype("int8")
y_train = train_df["tokyo_price_jpy_per_kwh"]
y_test = test_df["tokyo_price_jpy_per_kwh"]
# numpy 配列に変換
X_gam_train = X_gam_train.to_numpy()
X_gam_test = test_df.copy()
X_gam_test["is_holiday"] = X_gam_test["is_holiday"].cat.codes.astype("int8")
X_gam_test = X_gam_test[gam_features].to_numpy()
y_true_test = y_test.to_numpy()
※モデルに入力する値は数値特徴量に限られるので、カテゴリカル変数は整数にしておきます。
学習
gam.gridsearch(X_gam_train, y_train)
gam.summary()
LinearGAM
=============================================== ==========================================================
Distribution: NormalDist Effective DoF: 153.0956
Link Function: IdentityLink Log Likelihood: -789240.6544
Number of Samples: 140256 AIC: 1578789.5
AICc: 1578789.8412
GCV: 110.5696
Scale: 110.3524
Pseudo R-Squared: 0.2508
==========================================================================================================
Feature Function Lambda Rank EDoF P > x Sig. Code
================================= ==================== ============ ============ ============ ============
s(0) [0.001] 20 20.0 1.11e-16 ***
s(1) [0.001] 20 19.0 1.11e-16 ***
s(2) [0.001] 20 19.0 1.11e-16 ***
s(3) [0.001] 20 19.0 1.11e-16 ***
s(4) [0.001] 20 19.0 1.11e-16 ***
s(5) [0.001] 20 18.2 1.11e-16 ***
s(6) [0.001] 20 19.0 1.11e-16 ***
s(7) [0.001] 20 19.0 1.11e-16 ***
f(8) [0.001] 2 1.0 9.33e-01
intercept 1 0.0 6.08e-01
==========================================================================================================
Significance codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
WARNING: Fitting splines and a linear function to a feature introduces a model identifiability problem which can cause p-values to appear significant when they are not.
WARNING: p-values calculated in this manner behave correctly for un-penalized models or models with known smoothing parameters, but when smoothing parameters have been estimated, the p-values are typically lower than they should be, meaning that the tests reject the null too readily.
/tmp/ipykernel_119599/3358381670.py:1: UserWarning:
KNOWN BUG: p-values computed in this summary are likely much smaller than they should be.
Please do not make inferences based on these values!
この内容から、GAM は「データ全体の分散のうち約 25%(Pseudo R-Squared: 0.2508)を説明できている」ことが分かります。
つまり、需要・気温・日射・風速・季節性といったなめらかな構造はある程度捉えられている一方で、残りの 75% はスパイクや複雑な相互作用など、GAM の枠組みでは説明しきれていない部分が大きいと言えます。
なお、サマリの下に出ている Warning にもあるとおり、pyGAM の p 値まわりには既知のバグがあり、値が「実際よりも小さめに出やすい」ことが知られています。そのため、ここでは p 値や有意性コード(*** など)は参考程度にとどめ、主に Pseudo R-Squared からモデルの妥当性を判断することにしました。
また、違う観点から partial_dependence というplotでもモデルの妥当性を見ることができます。
import matplotlib.pyplot as plt
for i, term in enumerate(gam.terms):
if term.isintercept:
continue
XX = gam.generate_X_grid(term=i)
plt.figure()
plt.title(f"term {i}")
plt.plot(XX[:, term.feature], gam.partial_dependence(term=i))
plt.show()
これは、他の特徴を平均に固定した場合の「単独効果」を表しています。GAMの各termは厳密に加法構造であり、この形はそのまま寄与している形状と読むことができます。
term 0:demand(需要)
- 需要 40,000 kW を超えたあたりから 価格への寄与が急増している
- 55,000〜58,000 kW で スパイク的に影響が増加
⇒これは電力価格の 需給逼迫時の急騰 を非常によく反映している。GAM が 需要の急カーブ構造(S字→急増部分) をちゃんと捉えていると分かる
term 1:demand_7d_ma(需要の7日移動平均)
- 需要の基調(季節的水準)が上がると価格もじわじわ上がる
- 40,000 以上のベース需要の期間では寄与が大きい
⇒ スパイクではなく ゆっくりした基調トレンド を説明している
term 2:temperature(気温)
- 0〜10℃:暖房需要で価格が高い
- 10〜25℃:価格がやや低い(需要が少ない)
⇒ 30℃付近から急落(学習データでは「高温→太陽光多い→価格低下」が優勢?)
term 3:temp_7d_ma(気温の7日移動平均)
- 気温の基調が低い時は価格が高く、基調が高い時期は価格が低くなる
⇒ これは季節サイクル成分と関係していそうです
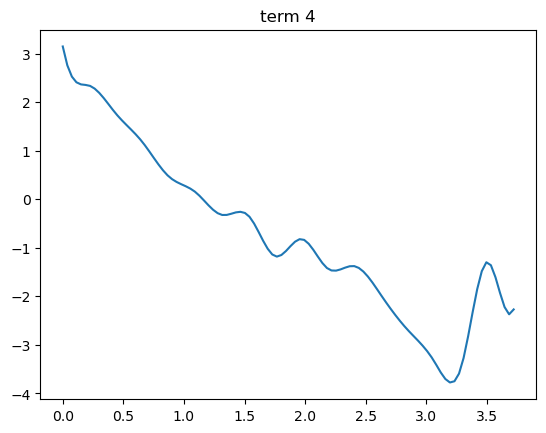
term 4:solar_radiation(全天日射)
- 日射量が増えると価格寄与は下がる(太陽光の余剰供給)
- 3.0 付近で最も下がり、その後やや上昇(極端な日射時のカットや逆潮流?)
⇒ 太陽光が活発になり価格が崩れるという現象を表しています
term 5:wind_speed(風速)
- 風速 12〜14 m/s 付近で価格寄与が急落(風力爆風 → 価格下落)
- それ以上で反発(風車停止域に入るため?)
⇒ 風力の可変性を反映した典型的な形状
term 6:hour(日中の時間帯、周期スプライン)
- 早朝(5–9時)にピークがあり価格寄与が高い
- 15–18時にも顕著な山がある(夕方ピーク)
- 深夜帯は低い
⇒ 1日の 需要カーブと太陽光の関係 を説明している
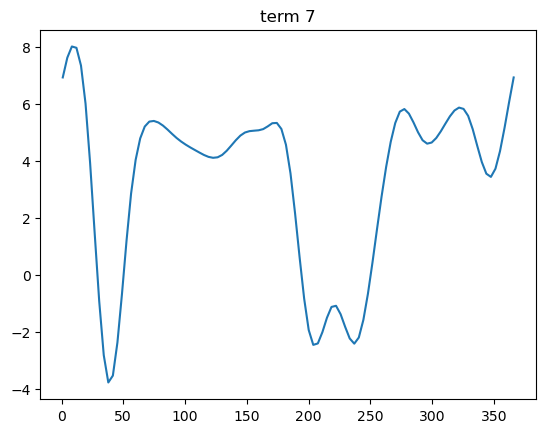
term 7:day_of_year(年周サイクル、周期スプライン)
- 1月上旬は高い(冬季需要)
- 2〜3月は下がる
- 7〜9月は再び上昇(夏の冷房)
- 秋に落ち着く
- 12月で再び上昇し始める
⇒ 年周需要構造 がそのまま出ている
term 8:is_holiday(休日フラグ)
- 休日(1)の方が若干価格寄与が小さい(需要が落ちる)
- 効果量は小さい(±0.03 程度)
⇒ 休日効果は需要ほど大きくないため妥当な形状
予測
train_df["y_gam"] = gam.predict(X_gam_train)
test_df["y_gam"] = gam.predict(X_gam_test)
y_gam_test = test_df["y_gam"].to_numpy() # GAMの特徴量
y_gamを特徴量として使っていきます。
残差も計算して残しておきます。
# 残差ターゲットを作成
train_df["resid"] = y_train - train_df["y_gam"]
test_df["resid"] = y_test - test_df["y_gam"]
1. GAMで予測 + 残差をLightGBMで予測
GAMで使った特徴量をLightGBMから削除すると精度が下がっため、すべての特徴量を学習に使用しています。
y_resid_train = train_df["resid"] # 残差学習のときの目的変数
y_resid_test = test_df["resid"]
feature_cols.remove("y_gam") # feature_colsにy_gamが含まれていた場合
X_train_lgb_resid = train_df[feature_cols]
X_test_lgb_resid = test_df[feature_cols]
- 残差の予測とgamの値を足し合わせて最終予測とします
y10_test = y_gam_test + pred_r10
y50_test = y_gam_test + pred_r50
y90_test = y_gam_test + pred_r90
結果
{'PICP(P10-P90)': 0.6871396769221988,
'MIW(P10-P90)': 7.1879688143492455,
'IntervalScore_80': 12.730858199588726,
'Pinball_p10': 0.559842759850748,
'Pinball_p50': 1.2839934665910062,
'Pinball_p90': 0.7132430601081245,
'CRPS_approx': 0.8523597621832929}
精度が全体的に悪化してしまいました。
本来は「GAM では表現しきれなかった構造(非線形・相互作用など)」を残差側で LightGBM に学習させる狙いでしたが、実際には残差に含まれるのはスパイクやランダムな変動が多く、学習に使える信号よりもノイズの比率が高かった と考えられます。
また、GAM の誤差構造(正規誤差+平滑化)が「外れ値をあまり重視しない」性質を持つため、残差だけを集めると「スパイクばかりが集まったデータ」を LightGBM に渡している状態になり、学習が難しくなっている可能性もあります。

全体的に動きが小さく、価格が大きく動く場面では激しく動きすぎて外しています。また、そのあとは予測がひと段階低すぎるようです。2 段構成にすると「GAM がベースラインを外した区間では、残差モデルも一緒に引きずられてしまう」ため、誤差が連鎖しやすい点も弱点です。
2. GAMで予測 + GAMの出力を特徴量の一つに加えてLightGBMで予測
lgm_features_addgam = feature_cols
lgm_features_addgam.append("y_gam")
X_train_lgb_addgam = train_df[lgm_features_addgam]
X_test_lgb_addgam = test_df[lgm_features_addgam]
結果
{'PICP(P10-P90)': 0.845482048062104,
'MIW(P10-P90)': 6.148285285284878,
'IntervalScore_80': 8.442088733835911,
'Pinball_p10': 0.3899675264161663,
'Pinball_p50': 0.8407276286485079,
'Pinball_p90': 0.4542413469674248,
'CRPS_approx': 0.5616455006773663}
LightGBM単体とそこまで変わりません。
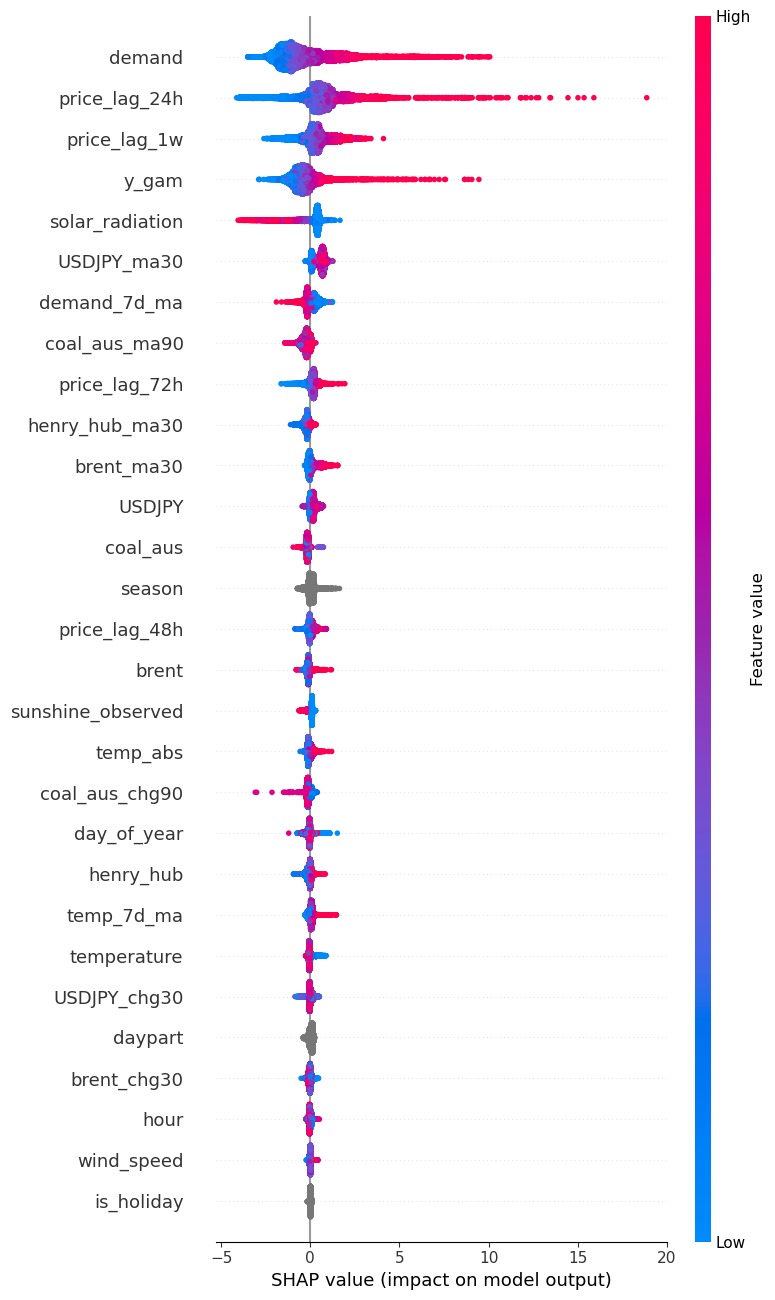
y_gamが4番目にきていることから重要な特徴量の一つになっていることが分かります。
意外ですが春の予測を外している一方、高騰する場面では追えているように感じます。
本番運用
今後行っていくリアルタイム予測では、未来を予報するため、今使っているような実際の値は使えません。つまり、予測値となるため必ずノイズが増えることになります。
GAM では、加法構造とスムージングが効いているため、入力が多少ノイジーでも、木モデルのように極端にギザギザした反応は出にくいという特徴があります。
そのため、なめらかなベースラインをy_gamとしてLightGBM渡すことでノイズの多い予測入力についても頑健になるのでは?という期待を込めて、GAMでの特徴量作成⇒LightGBMというモデルを採用したいと思います。
※本来ならば本番環境に合わせて訓練とテストでも予測値を使うべきですが、過去の天気予報はどうしても見つけられず、このような方針を取ります(´;ω;`)
明日
残差分析をして価格モデルがどのような場面で外れるかを見ていきたいと思います!