マインスイーパの解説に関する他の記事.
今回使用したマインスイーパの自作コード(マインスイーパのゲーム自体のクラスと確率分布を求めるためのクラス,実際に解いていくクラス).バージョンはpython3.8で使用したライブラリはnumpy (とoptionalでmatplotlib)のみなので簡単に動かせるはず.
ちなみに今回のエージェントの勝率は初級で97.4 %(= 9740/10000),中級で87.1 %(= 1742/2000),上級で45.3 %(= 181/400)という記録が出た.上級なら大概 2 択が発生するので,勝率はそんなとこだろうといったところ.
マインスイーパとは
マインスイーパとはWindows等にデフォルトで入っているゲームで地雷の入っているマスを除いたすべてのマスを開くというゲームである.熱狂的な支持者が多く,筆者も好きなゲームである.今回はこのゲームで良い勝率を出せるプレイヤーエージェントを作ろうという記事.ちなみに本来はJava,C,C++あたりでコードを組んで,高速化すべきだが,今回はとりあえずpythonでやってみた.
[追記]
今回のマインスイーパクラスの盤面初期化では現在のWindowsのデフォルトを再現するために初手のクリック前に盤面を決めず,初手クリック後にクリックした点及びそれに隣接する点には地雷を絶対に含めない盤面生成を行っている.(つまり,初手負けと初手で1マスしか開かないという可能性を除去している.)
戦略
地雷を置くことのできる場所には地雷を置き,地雷の情報から開けることのできるマスを開け,それでもわからない場合にとりあえず確率分布を求めて地雷踏む確率の小さなマスを開けるという戦略を取る.
ある1マスの周りに地雷が確実に入っている場所の推定
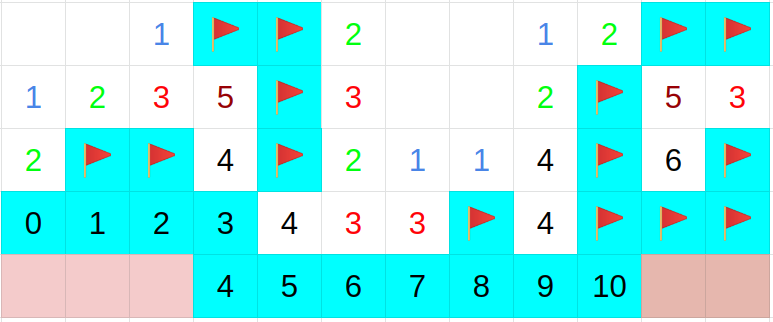
注目しているマスの周りの開いていないマスの数と注目しているマスに書いてある数字が一致していれば,それらの開いていないマスは全て地雷が入っている.つまり,下の1つ目の図の状態のときに開いていないマスにフラグを立てる.
図1 マスの周りが中心マスの数字と同じだけ開いていない例
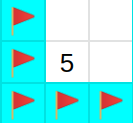
図2 図1の開いていないマスに対してフラグを立てたときの図
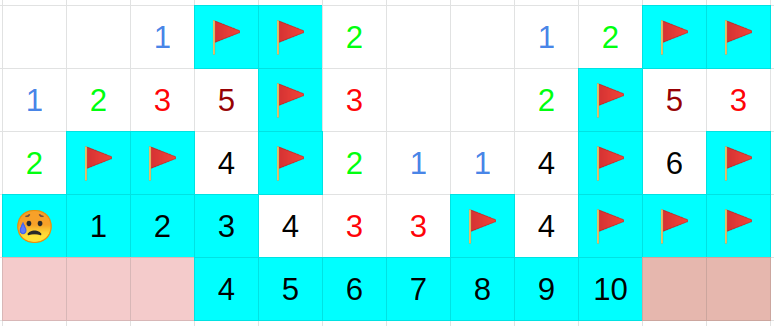
ある1マスの周りに地雷が確実に入っていない場所の推定
注目しているマスの周りの地雷が確定しているマスの数と注目しているマスに書いてある数字が一致していれば,それらの開いていないマスは全て地雷が入っていない.
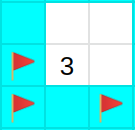
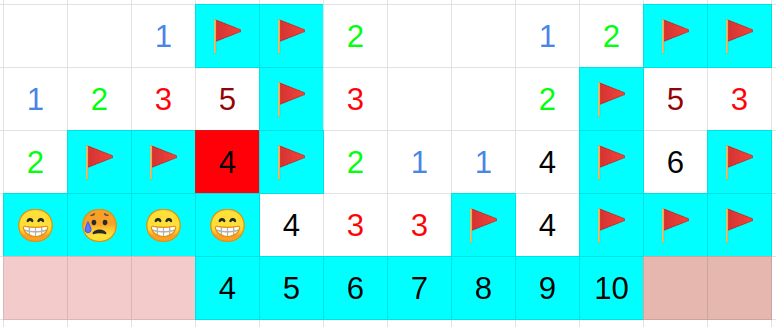
図3 中心のマスに書かれている数字分だけ周りにフラグが立っている例
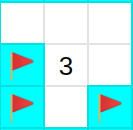
図4 図3のフラグが入っていないマスを開いたときの図
各マスに地雷が入っている確率の推定
マインスイーパの盤面を3進数(安全・地雷・地雷の仮定)によって表すことで考えうる盤面の全パターンを数え上げる.
確率の推定自体は安全に開くことのできるマスがなくなったときに行われる.
まず,フラグの立っていないマスに地雷を仮定し,その盤面に対してフラグを立てる操作とマスを安全に開ける操作を繰り返す.地雷を仮定した盤面において,フラグを立てる操作及びマスを開ける操作ができなくなったときにもう一度フラグの立っていないマスに地雷を仮定する.これらの操作を前の反復状態において既に開かれているマスと隣接する全てのマスが「安全」「地雷」「地雷の仮定」に分類されるまで繰り返す.全てのマスが分類されたら,地雷の仮定されているマスの内の一つを安全であるという仮定に変更して,もう一度全マスを分類する.これらの操作を可能な限りに繰り返す.
まず,用語をいくつか定義.
・未開:マスが開いていないこと.
・無人島:自分自身と隣接するマスがすべて未開であるマスもしくはその集団のこと.
step 1
確率分布を求めるための配列を作成.
この配列に情報を納めるマスは,「フラグが立っていない」「開いていない」「無人島でない」という条件を満たす.
つまり,図5の盤面でいうところの水色でかつフラグのないマスを対象に配列の情報を格納する.
次に対象のマスに対して図6のように通し番号を設定し,それらの通し番号をIndexとした,以下の配列(長さはいずれも対象となるマスお数だけ存在する)を作る.
- xs: マスの$x$座標.
- ys: マスの$y$座標.
- states: マスの状態.(0:安全,1:地雷,2:地雷を仮定,None:どれにも属さない)
- n_bombs: マスに地雷が入ると判定された回数
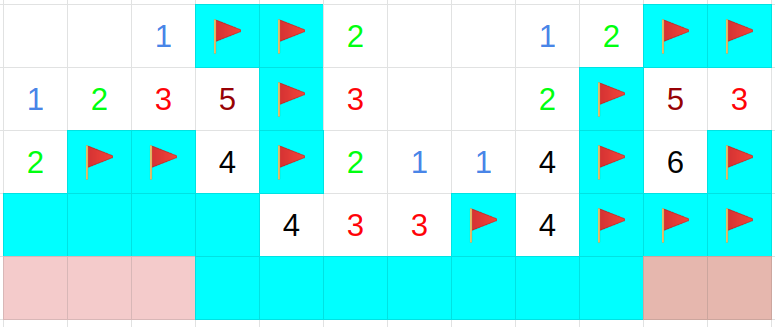
図5.新たなフラグを立てることも安全にマスを開けることもできない状況.
step 2
最初,statesの中身は全てNoneであるから,マスの通し番号が0であるマスの状態を「2(地雷を仮定)」として,フラグの建設と安全なマスの探索を行う.
step 3
フラグの建設もしくは安全なマスの探索がこれ以上進まない状態になったら,マスの状態がNoneであるマスのうち,マスの通し番号が最小であるマスの状態を「2」として,フラグの建設と安全なマスの探索を行う.
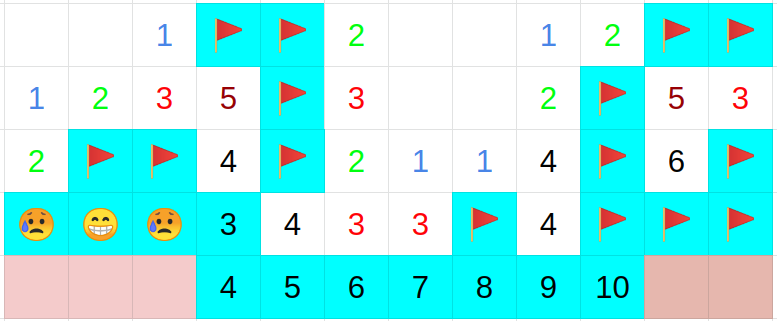
図8.通し番号2のマスは仮定に新たに地雷を仮定した際の盤面.
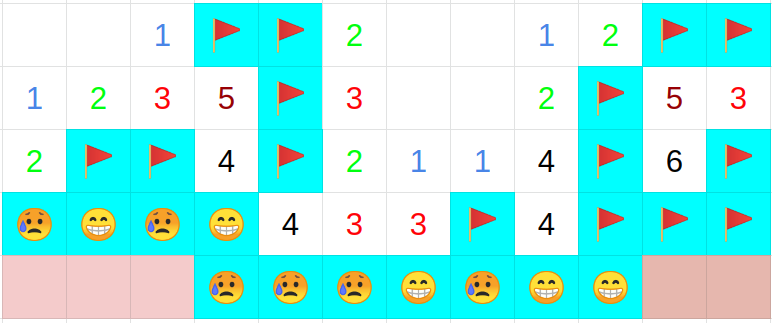
図9.通し番号1のマスに地雷を仮定したあと,地雷の仮定・安全マス・フラグの評価を繰り返したあとの盤面.
step 4
マスに書いてある数字に対して周囲のフラグ数が多いもしくは周囲の安全なマスの数が多い等の矛盾が生じたとき及び全てのマスの状態がNoneでなくなったときに新たな仮定を置いて盤面の探索を開始する.新たな盤面の探索をする際には地雷の仮定されているマスの内,最も大きな通し番号を持つマスを安全であるという仮定に変更して探索を開始する.図9で言うと通し番号2のマスを安全に変更して,通し番号3以上のマスを全てNoneに戻してから探索を再開する.
また,マスの状態が全てNoneではなくなった際にはn_bombsに以下の値を加える.
全体の地雷の個数とstatesが 1 or 2 である個数の差を $B$ とし,無人島に属するマスの個数を $L$ とする.Noneがなくなったとき,その盤面は無人島への地雷割当考慮なしでの一つのパターンとして完成している.そのため,その盤面でstatesが 1 or 2であるマスは盤面全体では無人島への地雷の割り当て方の組み合わせ個数(つまり,$B$個の地雷を$L$個のマスに割り当てる組み合わせの個数)だけ存在する.ゆえにn_bombsの該当する通し番号と全体の組み合わせ数$count$ に $ _L C_B $ を加える.
また,無人島の地雷カウント変数 $count_L$ に $_{L-1} C _{B-1}$ (つまり,自分自身に地雷を割り当てたあとに残りの地雷を他の無人島マスに割り当てる組み合わせ)を加える.
step 5
step 3 と step 4 をマスの状態から None と 2 が消え去るまで行う.消え去ったあとに,それぞれのマスの地雷判定回数を全体のパターン $count$ によって割ることで各マスに地雷が入っている確率を求めることができる.
version
1.0.0 2019/2/24
1.0.1 2019/2/25 マインスイーパクラスに関して追記
2.0.1 2022/2/4 gif動画を追加