はじめに
マインスイーパをアルゴリズムで解くことができないかを考察してみた。
みなさんご存じの通り、マインスイーパは常に確実に解けるわけではなく、確率的にしか解けない場合もある。ここで、マインスイーパを解くアルゴリズムは、以下の2つに分けることができる。
- 確実に分かる部分のみを解くアルゴリズム。解けない部分は人の手か、乱数による選択や別のアルゴリズムの助けを借りる必要がある。
- できるだけ高い確率で解くことを目指すアルゴリズム。
現状、1の、分かる部分のみを解くアルゴリズムを構築し、JavaScriptで実装し、完璧ではないものの、かなりいいところまで解かせることができている。
github上で公開しているので、こちらでお試しあれ。適当にクリックしてマスを開いたあと「Solve」をクリックすれば、確実に分かる部分を埋めてくれる。(動作確認はFirefoxでしか行っていないため、他のブラウザで動作しないおそれがあります。その際はご指摘下さい。)
盤面の取扱い
盤面の各マスは、0, 1, ..., (盤面の行数*列数) と、1つの正の整数で表すことができる。(x, y)と座標で取っても別によいが、ここでは、特に必要がないので、1つの正の整数で表すこととする。番号の付け方は好きにしても構わないが、私の実装では、
0 1 2 3 4
5 6 7 8 9
のように番号を取った。割と自然な方法だと思う。
マス目をクリックしたときの情報の取扱い
マス目をクリックすると「どこに」「何個の地雷が」あるかを知ることができる。このように「どこに」と「何個の地雷」がセットになった情報を「ヒント」と呼び、次のように表す。
例:
どこに→マス目 1, 10, 11
何個→2個 の場合
$(\{1, 10, 11\}, 2)$ と表現する。
$(A, a) = (\{1, 10, 11\}, 2)$と表現した場合、$A = \{1, 10, 11\}, a = 2$を意味し、$|A|$は、Aに含まれるマス目の数を意味する。(この例の場合は3)
また、$(\{A_1, A_2, ..., A_n\}, a) = (\{1, 10, 11\}, 2)$と表現した場合、$A_1 = 1, A_2 = 10, A_3 = 11$を意味する。
列数が10の盤面で、マス目 0 をクリックして、周りの地雷の数が2と出た場合、次のヒントが得られたことになる。
({1, 10, 11}, 2)
({0}, 0)
ひとつめは、{1, 10, 11}の中に地雷が2個あるという意味で、
ふたつめは、0をクリックした結果、地雷ではなかったのだから、0は地雷ではないことを示したものである。
0 1 2 3 ... 8 9
10 11 12 13 ... 18 19
20 21 22 23 ... 28 29
...
同様に、12をクリックして周りの地雷の数が1と出た場合は、
({1, 2, 3, 11, 13, 21, 22, 23}, 1)
({12}, 0)
が得られる。
「最小のヒント」、「最大のヒント」、「不要のヒント」
({0}, 0), ({12}, 0), ({5}, 1) のように、{}の中にたった1つのみのマス目を持ち、そこに含まれる地雷の数が0または1であるヒントを「最小のヒント」と呼ぶ。
盤面のすべてのマス目の集合をX (|X| = 列数*行数)、地雷の総数をNとするとき、ヒント(X, N)を「最大のヒント」と呼ぶ。最大のヒントは、マス目を何もクリックしていないときから分かっている唯一のヒントである。
({}, 0)と表されるヒントを「不要のヒント」と呼ぶ。何の情報ももたらさず、存在してもしなくても同じである。実用上は、不要のヒントが多くあると配列のサイズが大きくなって計算時間の無駄であるが、ヒントを削除する代わりに不要のヒントに置き換えると配列の要素数を変えずに済むという使い道もある。
マインスイーパのクリアの定義
新たなヒントを得ることにより、また、得られたヒントを分解することにより、すべてのマス目に関する最小のヒントが得られた場合に、マインスイーパをクリアしたと表現する。
なぜならば、このとき、任意のマス目nに対し、({n}, m), m = 0 or 1が得られ、mが0ならばそのマス目は地雷ではなく、mが1ならばそのマス目は地雷である、と明確に分かるからである。
ヒントの分解
次のようにして、ヒントを分解する。
自明な分解
-
$(\{A_1, A_2, ..., A_n\}, 0)$は、次のn個のヒントに分解できる。
$(\{A_1\}, 0),\ (\{A_2\}, 0),\ ...,\ (\{A_n\}, 0)$ -
$(\{A_1, A_2, ..., A_n\}, n)$は、次のn個のヒントに分解できる。
$(\{A_1\}, 1),\ (\{A_2\}, 1),\ ...,\ (\{A_n\}, 1)$
2つのヒントの関係
2つのヒント$(A,\ a),\ (B,\ b)$について、以下のように分解できる。
ヒントの内包
- $A \subset B$のとき、$(B,\ b)$は分解され、$(B', \ b') = (B-A,\ b-a)$を得る。ここで$B-A$は、Bに含まれるがAには含まれないマス目の集合を表している。
- 同様に$A \supset B$のとき、$(A,\ a)$は分解され、$(A',\ a') = (A-B,\ a-b)$を得る。
2つのヒントの3分割
- $C = A\cap B$とおく。
$max(0, a-|A-C|, b-|B-C|) = min(|C|, a, b)$のとき、$(A,\ a)$, $(B,\ b)$は分解され、次の3つのヒントを得る。
$(A',\ a') = (A-C,\ a-c)$, $(B',\ b') = (B-C,\ b-c)$, $(C,\ c)$, ただし$c = min(|C|, a, b)$とする。
このヒントの3分割は、max(0, a-|A-C|, b-|B-C|)がcの下限を、min(|C|, a, b)がcの上限を表している。上限と下限が一致したときに限り、cを決定することができ、分解が可能となる。具体的な状況としては、以下を想定している。
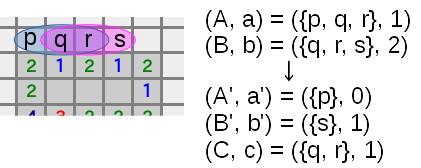
ここでは、マス目を数字のかわりにp, q, r, sとした。
qの下のマス目が与えたヒントをA, rの下のマス目が与えたヒントをBとしたとき、上図のように分解でき、pとsとの地雷の有無が決定する。
今後の課題など
ここまでが、現時点でできている、マインスイーパのモデルである。
分かっているヒントを分割し、最小のヒントから地雷ではないと確定したマス目を開き、新たなヒントを得ることを繰り返すことで、マス目を分かる限り開くことができる。
現時点で、以下が、よく分かっていない。
-
ヒント比較の順序を考慮する必要性:
2つのヒントの比較順序により、分解結果は変わるか。また、変わるのはどういった場合か。最大のヒントが関わっている場合のみに変わるのか、それ以外でも変わるのか。 -
分解前のヒントは削除すべきでないか:
現状の実装では、簡単に無限ループを避ける手段として、分解前のヒントは削除している。分解後のヒントから分解前のヒントを導けるので情報量は減っておらず、ゆえに削除に問題ないと考えている。だが、もしも削除しないことでヒント比較の順序を考慮せずに済むのであれば、残すべきかもしれない。 -
他のヒント分解の方法:
他にはないと思っているが、あるかもしれない。 -
ヒントから、あるセルが地雷である確率を求める手法:
最初に挙げた2種類のアルゴリズムのうち、2番目の、できるだけ高い確率で解くことを目指すアルゴリズムに展開する場合、分かるものがなくなったときは、最も地雷である確率が低いものを開く、という戦略が考えられる(他にも、どんなヒントが得られれば嬉しいかで開く箇所を決める戦略もありうるが、非常に難しそう)。どのようにしたら確率が分かるか。
理論家、アルゴリズマー諸氏のアイディアや挑戦もお待ちしております。