画像クリックで遊べます。
みなさんは勝てましたか?
作り方を解説していきます。
方針
世の中には強いオセロ AI がたくさんあります。ブラウザ js で動く強豪 AI も既にあります。
(参考: http://el-ement.com/blog/2017/02/20/reversi-ai/)
今回はゲーム AI の仕組みを理解することを目的として、以下の方針で作りました。
- 簡単に実装できる (ゲーム AI として最小限のコンポーネントのみを備える)
- そこそこの強さ (人間初心者に負けないくらい、できれば自分より強くしたい)
全体像
ゲーム AI は概ね以下の部品を持っています。
- 静的評価関数
- 探索処理
- ビットボード (軽量で高速に処理可能な局面データ構造)
静的評価関数は、局面のスコアを計算する関数です。膨大な回数実行されるため、スコアの正確性と処理の軽量さのトレードオフをうまくとる必要があります。
探索処理は文字通りゲーム木を辿る処理です。
ビットボードはオセロの局面を管理するデータ構造です。局面をビット列とみなして 1 つか複数の int に押し込んでしまいます。データサイズが軽くなるだけでなく、局面に対する演算 (合法手列挙、着手、白黒反転など) をプリミティブなビット演算で行えるようになり、高速処理可能となります。
それぞれの部品について説明します。
静的評価関数
静的評価関数はある局面が自分にとって有利な度合いを表す関数です。一般に 0 点が形勢互角な状態、プラスなら自分が有利な状態、マイナスなら相手が有利な状態を表すように設計します。
ゲーム AI では一般に静的評価関数をゲーム木の末端に適用します。つまり、次の 1 手を直接評価するのではなく、探索処理によってあらかじめ決めた深さ (n 手先) まで潜り、その局面に対して静的評価関数を適用します。
強豪 AI は静的評価関数のパラメータを膨大な棋譜データからの機械学習や強化学習で調整しています。盤面を様々な部分形に分割し、学習済みパラメータで部分形をスコアリングし、その累積和を最終的なスコアとしているようです。
今回は実装を簡単にするため、以下のようにシンプルなスコアリングとしました。着手可能数は次の一手を指せる場所の数です。
A = 自分の着手可能数 - 相手の着手可能数
B = 自石の四隅周辺の形の良さ - 相手石の四隅周辺の形の良さ
k = 適当な係数
スコア = A + kB
こんな定義でも探索で 6 手先くらいまで潜れば意外と強くなります。
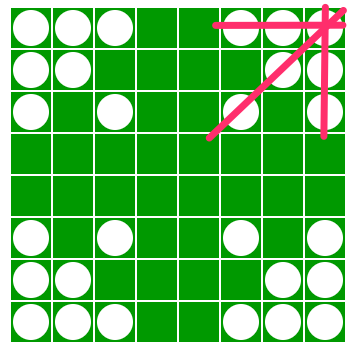
四隅周辺の形の良さについて
角から 3 マスの石の有無について、スコアを割り振っていきます。
スコアは感覚で恣意的に決めます。
これを全組み合わせ (2^3 = 8) 定義します。
実際のスコア計算では、図のように各四隅の縦横斜めを切り取り、スコアを合計します。
探索処理
探索処理では n 手先に潜って静的評価関数を適用します。n 手先のスコアを元に n - 1 手先のスコアを決め、n - 1 手先のスコアを元に n - 2 手先のスコアを決め…、という風に再帰的に処理を行い、最終的に次の 1 手のスコアを決めます。
この再帰処理では、自分も相手も常に最善手を指すことを仮定します。つまり、自分の手番ではスコアが最も高い手を選び、相手の手番ではスコアが最も低い手 (相手にとって最も高い手) を選びます。
n 手先が自分の手番だとすると、以下のようになります。
n-1手目 = max(n手目A, n手目B, ...)
n-2手目 = min(n-1手目A, n-1手目B, ...)
n-3手目 = max(n-2手目A, n-2手目B, ...)
このようなスコアリング手法はミニマックス法と呼ばれています。
今回はミニマックス法の改良版で計算不要な枝をカットするアルファベータ法と呼ばれる処理を実装しました。アルファベータ法はとても簡単に実装できます。
function alphaBetaEval(board: Board, depth: number, a: number, b: number): number {
// leaf node
if (depth <= 0) return evaluate(board)
const movables = Move.movables(board)
// pass
if (movables.length == 0) return -alphaBetaEval(reverse(board), depth - 1, -b, -a, tl)
for (const move of movables) {
const next = reverse(Move.move(board, move.x, move.y))
a = _.max([a, -alphaBetaEval(next, depth - 1, -b , -a, tl)])
if (a >= b) return a
}
return a
}
終盤完全読み
オセロは序盤中盤は石の数よりも配置が重要なゲームです。しかし最終的には石の数を最大化する必要があります。
今回は、ラスト 12 手 (空きマスが 12 箇所になった状態) になった時点で評価関数・探索処理を切り替え、最終局面まで全探索し自石数を最大化するようにしています。
反復深化
探索深さを決めるのは難しい問題です。同じ探索深さでも合法手が多い局面ではゲーム木が大きくなり、計算時間が長くなります。
実際のゲーム AI ではユーザー体験やルール上の制約のために、計算時間の上限を設ける必要があります。これを実現するのが反復深化と呼ばれる手法です。
反復深化はとても単純です。まず探索が必ず時間内に終了するであろう最小深さ k をあらかじめ決めておきます (今回は k=3 としました)。深さ k で探索し、終了したら深さ k + 1 で探索します。まだ時間が余っていたら k + 2 で探索する、という風に残り時間がある限り深さを 1 つずつ大きくしていきます。時間が無くなった時点で探索を打ち切り、最後に探索が完了した深さのスコアを結果とします。
今回は 500 ms で探索を打ち切るようにしました。ほとんどの局面で深さ 6 程度まで探索できるようです。
function iterativeDeepning(board: Board): MoveScore[] {
const movables = Move.movables(board)
const timelimit = Date.now() + TimeoutMS
for (let depth = 3;; depth++) {
try {
score: -alphaBetaEval(reverse(Move.move(board, place.x, place.y)), depth - 1, -MaxScore, -MinScore, timelimit)
} catch {
console.log(`depth: ${depth}`)
break
}
}
}
ビットボード
探索処理・静的評価関数の中で効率的に局面に対して演算を行うためのデータ構造です。オセロでよく用いられるのは、2 つの 64 bit 整数で黒石・白石の 64 マスの有無を表現する手法です。
この方法だと 64 マス全てに対する着手可能性判定が数十回のビット演算で出来てしまうようです。すごい…。
http://d.hatena.ne.jp/ainame/20100426/1272236395
今回は実装が面倒くさかったため簡易な手法を選びました。各マスの状態 (黒・白・空き) を 2 bit で表し、8 マスの並び 2 * 8 = 16 bit を 1 つの整数としてエンコードします。これを縦横斜めにそれぞれ保持します。
8 マスの全組み合わせ (3^8 = 6561) に対して着手時の石の返り方を事前計算してテーブルに持っておくことで、探索・評価時に毎回計算することを回避しています。
まとめ
シンプルな構成でそこそこの強さの AI を作ることができました。ただし評価関数がキモで、恣意的にパラメータを決めているため AI のクセが出やすいようです。
実際に自分が対局すると勝率 5 割程度ですが、勝った対局では四隅を取らせて辺を奪うような結果が多いです。辺の形が評価関数に反映できていないためだと思います。
辺の形を反映するように評価関数を設計し直すと改善するはずですが、ここから先の職人芸的なチューニングのことを考えると、強豪 AI のように機械学習してしまった方が実は簡単なのかもしれません。
今回はオセロ AI の仕組みを扱いましたが、将棋やチェスの AI も基本的には同じ仕組みで動いているようです。いつか時間を見つけてトライしたい。