基本の作図
例えばこんな感じのデータフレームがあったとする.
x y
0 2 0.954025
1 3 0.146810
2 1 0.409961
3 1 0.164558
4 3 0.782152
5 2 0.905869
6 3 0.210528
7 1 0.437970
8 1 0.801206
9 3 0.089576
10 2 0.960357
11 2 0.670732
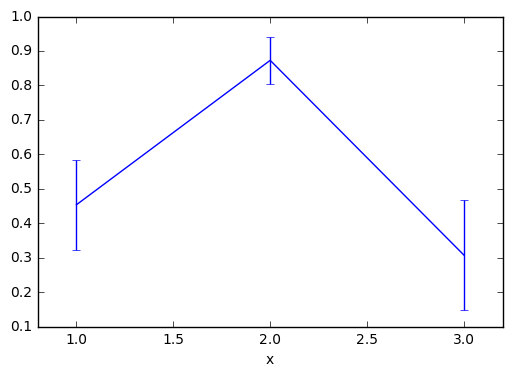
このデータフレームから標準誤差付きの図を描こうとすると,こんな感じ.
import numpy as np
import matplotlib.pyplot as plt
m = df.pivot_table(index='x', values='y', aggfunc='mean')
e = df.pivot_table(index='x', values='y', aggfunc='sem')
m.plot(xlim=[0.8, 3.2], yerr=e)
このように,yerrに誤差の大きさを指定することで,誤差棒を作成することができる.
信頼区間を用いた作図
そこで,信頼区間の長さを求めるcilenを定義して利用することにする.
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def cilen(arr, alpha=0.95):
if len(arr) <= 1:
return 0
m, e, df = np.mean(arr), stats.sem(arr), len(arr) - 1
interval = stats.t.interval(alpha, df, loc=m, scale=e)
cilen = np.max(interval) - np.mean(interval)
return cilen
m = df.pivot_table(index='x', values='y', aggfunc='mean')
e = df.pivot_table(index='x', values='y', aggfunc=cilen)
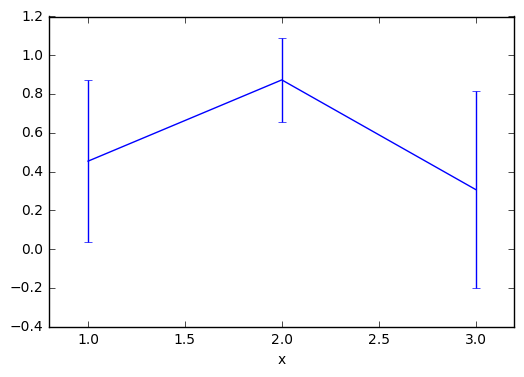
m.plot(xlim=[0.8, 3.2], yerr=e)
信頼区間付きの図を作成することができた.
おまけ
信頼区間を計算する方法は「nかn-1か」問題のせいでごちゃごちゃしてます.
「車輪の再発明は避けよ」に従って,とりあえず「信頼区間 Python」とかで検索した人は,
あたりを見て,微妙に違うことに困惑しつつも両方試してみて,そして結果が違うことに辟易することになると思います (なりました).
Rと同じ答えになるのは1の方.違うのは2の方です.ちょっと試してみます.
> x <- c(1, 1, 3, 3)
> t.test(x)
One Sample t-test
data: x
t = 3.4641, df = 3, p-value = 0.04052
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.1626138 3.8373862
sample estimates:
mean of x
2
1の方法
import numpy as np
from scipy import stats
alpha = 0.95
data = [1, 1, 3, 3]
mean_val = np.mean(data)
sem_val = stats.sem(data) # standared error of the mean
ci = stats.t.interval(alpha, len(data)-1, loc=mean_val, scale=sem_val)
print(ci)
>> (0.16261376896260105, 3.837386231037399)
2の方法
import math
import numpy as np
from scipy import stats
alpha = 0.95
data = [1, 1, 3, 3]
mean_val = np.mean(data)
std_val = np.std(data)
ci = stats.t.interval(alpha,len(data)-1,loc=mean_val,scale=std_val/math.sqrt(len(data)))
print(ci)
>> (0.40877684735786857, 3.5912231526421312)
今回は天下のRに従うことにしたので1を採用しています.
なお,2は何が違うのかというと,ciを計算する箇所の最後の方
math.sqrt(len(data))
これです.nで割ってます.しかし推測統計を行うのであればn-1で割った方が良いです.t分布を仮定するからですね.実際,
math.sqrt(len(data) - 1)
とすると,方法2の答えもRと完全に一致します.