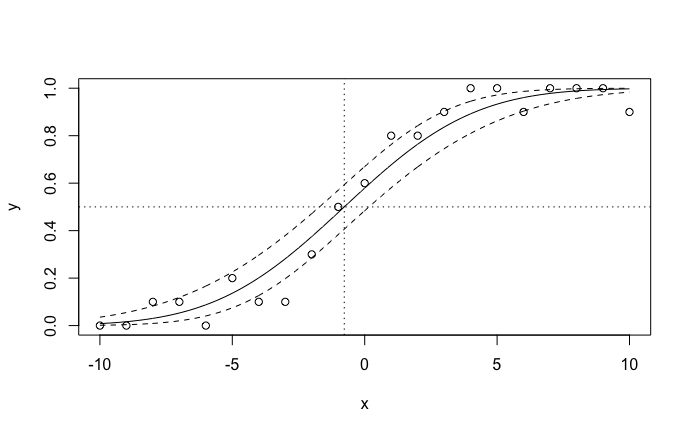
心理系なら誰もが一度はやってみたいprobit分析.
最近図を作る機会があったのでメモ.多分これが一番早いと思います.そして一番無骨…
# ===== 累積正規分布にだいたい従うぐらいの適当なデータを生成する =====
x <- rep(seq(-10, 10), 10)
y.true <- pnorm(x, mean = 0, sd = 3)
y <- ifelse(y.true + rnorm(length(x), sd = 0.3) >= 0.5, 1, 0)
d <- data.frame(x, y)
# ===== プロビット回帰して予測値を算出する =====
model <- glm(y ~ x, family = binomial(probit), data = d)
summary(model)
x <- seq(-10, 10, length = 1000)
y.probit <- predict(model, data.frame(x), type = 'link', se.fit = TRUE)
y <- pnorm(y.probit$fit)
plot(x, y, type = 'l', xlim = c(-10, 10), ylim = c(0, 1)) # 図中の実線
# ===== 両側95%信頼区間を図に加える =====
interval <- qnorm(0.975, 0, 1) * y.probit$se.fit
lines(x, pnorm(y.probit$fit + interval), lty = 2) # 図中の破線 (上側)
lines(x, pnorm(y.probit$fit - interval), lty = 2) # 図中の破線 (下側)
# ===== PSE (主観的等価点) を求めて50%閾値に線を引く =====
pse <- as.vector(-coefficients(model)[1] / coefficients(model)[2])
abline(h = 0.5, lty = 3) # 図中の点線 (横線)
abline(v = pse, lty = 3) # 図中の点線 (縦線)
# ===== 実験条件ごとに平均値を算出して散布図を書く =====
y <- tapply(d$y, d$x, mean)
x <- names(y)
points(x, y) # 図中の散布図
- プロビット回帰自体は
glmで二項分布仮定してリンク関数を累積正規分布に設定するだけです - たとえ1変量の回帰モデルであっても,predictに直接説明変数xのベクトルを与えることはできないようです.ので,xという列を持つデータフレームに変形しておく必要があります
- predict時に
type = responseとすると累積確率が,type = linkとするとプロビット値が,type = predictionとすると01の予測値が返ってきます.すごい楽- 要は
predict(..., type = 'response') == pnorm(predict(..., type = 'link'))predict(..., type = 'predict') == predict(..., type = 'response') >= 0.5
- カーブをプロットするだけなら
type = reponseで良いけど,信頼区間の計算が手間なので,一旦type = linkでプロビット値の予測値を出し,必要なタイミングでpnormを使い累積確率に変換するほうが楽そう
- 要は
- predict時に
se.fit = TRUEにするとプロビット値の標準誤差を計算してくれます.なので,「プロビット値 ± 1.96 * 標準誤差により上下信頼区間を計算する」「その値をpnormでくくる」の2ステップで累積確率の信頼区間を求めることができます- 「
predict(..., type = 'response')で直接 (プロビットではなく) 累積確率のy$fitとy$se.fitを出し,y$fit + 1.96 * y$se.fitで上下信頼区間を求める」とこの2ステップを逆順に行うことになります.この方法は結構色んな記事で見かけますが,pnormは非線形な変換なので,ホントはダメなんじゃないかなぁ.そもそもそのような方法を使ってしまうと,せっかくbinomialを仮定したのに信頼区間が01の範囲外に出る可能性がありますよね
- 「
- PSEが
-coefficients(model)[1] / coefficients(model)[2]で計算できる理由は九大の先生が詳しく説明してくれています - 最後から二行目では
tapplyで作ったテーブルのnamesを取得しx軸としています.このxは実際には文字列なのだけど,なぜかpoints時に普通に数値に変換されてプロットできます - PSE算出後,たいていの研究ではPSEに対する実験要因の効果を分散分析することになります.いち意見ですが,PSEの分散分析は,刺激量と実験要因を説明変数としたGLMやGLMMと比較して以下の利点と欠点があります
- 長所1: 「主観的に等価と感じる点」が人によって違うかどうかを問題とする場合,結果の解釈がおそらく最も容易である
- 長所2: 頑健さが経験的に示されてきた心理物理学の手法にしたがう分析である
- 短所: PSE以外の情報がすべて捨てられるため,刺激量と実験要因の交互作用を分析できない.したがって,たとえば次のような可能性については言及できない: ある実験操作は判断に自信がある場合 (01付近) にのみ影響する
普段Pythonを使っていますが,たまにR使ってみると早くていいですね.