本コンテンツは機械学習入門講座を各所でやっている内容の一部を、受講者の皆様の予習・復習のために公開しているものです。対象読者は、Pythonをやったことがほとんどない方やつまづいてしまっている方でも概ね実行できるようになるレベルで書いています。解説は講座でそれなりに詳しくしているため、コードにコメントする以上の説明はあまり記述していません。
各コードはJupyterシリーズやiPythonで記述しながら実行できるように記述しています。
AI/DX/機械学習/Pythonのアドバイザリー、社内研修、セミナー等承っております。
webサイトからお問い合わせください。
BeeComb Grid株式会社
機械学習入門シリーズ記事
- 機械学習入門 vol.1 Pythonの基礎1 記述とデータ型 -> 講座第3回に相当
- 機械学習入門 vol.2 Pythonの基礎2 条件分岐と処理 -> 講座第3回に相当
- 機械学習入門 vol.3 Pythonの基礎3 関数・クラス・モジュール -> 講座第3回に相当
- 機械学習入門 vol.4 表(Pandas)の基本操作 -> 講座第3回/第4回に相当
- 機械学習入門 vol.5 グラフ(Seaborn)の基本操作 -> 講座第3/4回に相当
- 機械学習入門 vol.6 回帰 - 線形回帰 -> 講座第4回に相当
- 機械学習入門 vol.7 回帰 - ランダムフォレストとパラメータチューニング -> 講座第4回に相当
- 機械学習入門 vol.8 回帰 - その他の回帰 (k近傍法,ラッソ回帰,リッジ回帰..etc) -> 講座第4回に相当
- 機械学習入門 vol.9 判別(分類) -> 講座第5回に相当
- 機械学習入門 vol.10 次元削減 -> 講座第6回に相当
- 機械学習入門 vol.11 クラスタリング -> 講座第6回に相当
機械学習入門 vol.10 次元削減
次元削減のお話です。講座ではPCAとランダム写像、t-SNEを実践しました。次元削減をすることによって、PCAによる要素同士の重要度などを見ていくこともできますし、PCAで説明変数をまとめていくことで機械学習のトレーニングの計算コストを削減することもできます。また、よく高次元のデータを2次元・3次元に変換してデータの分布具合をグラフで見ることができるという使い方もされます。
import numpy as np
import pandas as pd
import seaborn as sb
from sklearn.decomposition import PCA
ボストンデータセットを読み込みます。
# ボストンデータセット
from sklearn import datasets
boston = datasets.load_boston()
boston
データフレームに格納します。
# データフレームに格納
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['Price'] = boston.target
df
PCA(主成分分析)
PCAのクラスを使って次元削減します。クラスのドキュメントはsklearn.decomposition.PCA本家をご確認ください。引数n_componentsはキープするコンポーネント、つまり削減後の次元数だと思ってください。
講座では時間の関係上いきなり2次元まで落とすコードだけ紹介しましたが、10次元以上のものをいきなり何の分析もしないで2次元まで落とすようなことは意図がない限り滅多にありません。
# PCA(主成分分析)を使って次元を2次元に削減
pca = PCA(n_components=2)
vectors = pca.fit_transform(df)
vectors
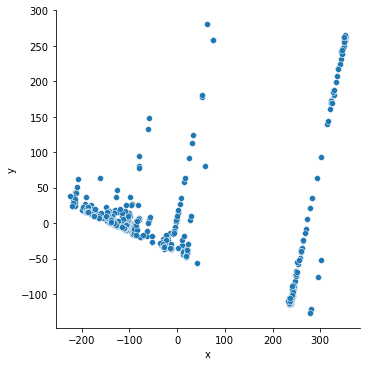
削減したベクトルを二次元空間上に配置してみてみましょう。全ての点が重ならないように2次元に圧縮されている様が見て取れます。
# 散布グラフで表示
dfv = pd.DataFrame(vectors, columns=["x","y"])
sb.relplot(x="x", y="y", data=dfv)
計算された固有ベクトルや主成分の分散、寄与率などを見てみましょう。
print('寄与率(%): ', pca.explained_variance_ratio_)
print('累積寄与率(%): ', np.cumsum(pca.explained_variance_ratio_))
print('固有値(主成分の分散): ', pca.explained_variance_)
print('固有ベクトル(主成分の方向): ', pca.components_)
ランダム写像
ランダム写像のクラスはsklearn.random_projection.SparseRandomProjectionを使います。詳しいパラメータは公式ドキュメントを確認してください。
ランダム写像は、次元上で「光点」と「背景幕」を用意して写った影を見ることで次元を一つ落とすという手法です。3次元である人に光を当てると後ろの壁に写った影は2次元になるというような理屈です。
# ランダム写像インポート
from sklearn.random_projection import SparseRandomProjection
rp = SparseRandomProjection(n_components=2)
vectors = rp.fit_transform(df) # ランダムだけに毎回結果は変わるので試行錯誤が必要
vectors
散布図で表示してみましょう。
# 散布グラフで表示
dfv = pd.DataFrame(vectors, columns=["x","y"])
sb.relplot(x="x", y="y", data=dfv)
固有値を見てみましょう。
print('固有ベクトル: ', rp.components_)
print('デンシティ: ', rp.density_)
print('写像フィット時の要素の数: ', rp.n_features_in_)
t-SNE
t-SNEを使ってみます。詳細な引数はsklearn.manifold.TSNEの公式ドキュメントをご覧ください。
t-SNEは、ものすごく簡単に言ってしまうと「高次元上でのデータ同士の距離をできるだけ損なわないように次元を削減する」ことを目的とし、次元削減に当たって確率分布にt分布を用いることからt-SNEと呼ばれます。
難しいことを書きましたが、PCAやランダムプロジェクションなどは次元削減時に「本当は距離が近いデータでも遠く映ってしまう」ことが頻繁に発生してしまうため、これを解決するための手法として利用されます。(要するにデータ同士の類似度を損なわないで次元を落としたい)
プログラムは下記の通りです。
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2)
vectors = tsne.fit_transform(df)
vectors
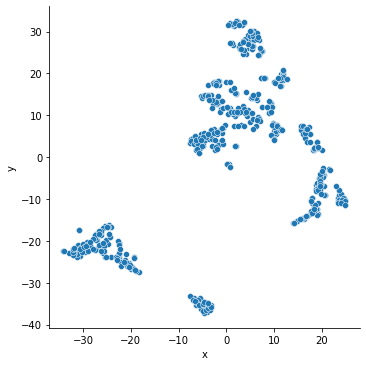
散布図で表示してみましょう。
# 散布グラフで表示
dfv = pd.DataFrame(vectors, columns=["x","y"])
sb.relplot(x="x", y="y", data=dfv)
MDS(多次元尺度構成法)
多次元尺度構成法(MDS)にはsklearn.manifold.MDSクラスをインポートして使います。MDSはデータ同士の距離や類似度・非類似度などをベースに次元を削減する手法です。
from sklearn.manifold import MDS
mds = MDS(n_components=2)
vectors = mds.fit_transform(df)
vectors
散布図を表示してみてみましょう。
# 散布グラフで表示
dfv = pd.DataFrame(vectors, columns=["x","y"])
sb.relplot(x="x", y="y", data=dfv)
機械学習入門シリーズ記事
- 機械学習入門 vol.1 Pythonの基礎1 記述とデータ型 -> 講座第3回に相当
- 機械学習入門 vol.2 Pythonの基礎2 条件分岐と処理 -> 講座第3回に相当
- 機械学習入門 vol.3 Pythonの基礎3 関数・クラス・モジュール -> 講座第3回に相当
- 機械学習入門 vol.4 表(Pandas)の基本操作 -> 講座第3回/第4回に相当
- 機械学習入門 vol.5 グラフ(Seaborn)の基本操作 -> 講座第3/4回に相当
- 機械学習入門 vol.6 回帰 - 線形回帰 -> 講座第4回に相当
- 機械学習入門 vol.7 回帰 - ランダムフォレストとパラメータチューニング -> 講座第4回に相当
- 機械学習入門 vol.8 回帰 - その他の回帰 (k近傍法,ラッソ回帰,リッジ回帰..etc) -> 講座第4回に相当
- 機械学習入門 vol.9 判別(分類) -> 講座第5回に相当
- 機械学習入門 vol.10 次元削減 -> 講座第6回に相当
- 機械学習入門 vol.11 クラスタリング -> 講座第6回に相当
AI/DX/機械学習/Pythonのアドバイザリー、社内研修、セミナー等承っております。
webサイトからお問い合わせください。
BeeComb Grid株式会社