機械設計で使用する数式をまとめておきます。式はlatexで書いてあるのでコピペで使用可能です。
また、式とパラメータはpythonで記載するので、流用可能です。あとは、絵が欲しいなぁ
熱応力
-
一軸拘束
$$
\sigma_{11}=- \alpha E(\Delta T)
$$ -
二軸拘束
$$
\sigma_{11}=-\frac{\alpha E}{1-v}(\Delta T)
$$
$$
\sigma_{11}=\sigma_{22}
$$
- 三軸拘束
$$
\sigma_{11}=-\frac{\alpha E}{1-2 v}(\Delta T)
$$
$$
\sigma_{11}=\sigma_{22}=\sigma_{33} \
$$
paramater_dict= {
'E':['縦弾性係数','[MPa]'],
'v':['ポアソン比',''],
'ΔT':['温度差','[K]'],
'α':['線膨張係数','[10^-6 K^-1]'],
'σ11':['熱応力','[MPa]'],
}
E = 1
v = 0.3
ΔT = 1
α = 1
σ11=-α*E*ΔT#一軸拘束
σ11= (α*E*ΔT)/(1-v)#二軸拘束
σ11= (α*E*ΔT)/(1-2*v)#三軸拘束
print(σ11)
ボルトのトルクと軸力計算
$$
T=\frac{F}{2}(\frac{d_2}{\cos \alpha}\mu_{s}+\frac{P}{\pi}+d_{W} \mu_{W})
$$
$$
F=\frac{2T}{\frac{d_2}{\cos \alpha}\mu_{s}+\frac{P}{\pi}+d_{W} \mu_{W}}
$$
$$
d_{W} = \frac{2(d_0^3-d_h^3)}{3(d_0^2-d_h^2)}
$$
paramater_dict= paramater_dict= {
'F':['ボルトの軸力','N'],
'P':['ピッチ','mm'],
'T':['トルク','N・mm'],
'd2':['ねじの有効径','mm'],
'dW':['等価摩擦直径','mm'],
'α':['ねじ山の半角(通常は30°)','°'],
'μW':['座面摩擦係数',''],
'μs':['ねじ面の摩擦係数',''],
'd0':['ボルト座面外径','mm'],
'dW':['等価摩擦直径','mm'],
'dh':['ボルト孔径','mm']
}
import math
F = 10
P = 10
d2 = 10
dW = 10
α = 30
μW = 10
μs = 10
d0 = 15
dh = 12
T=F/2*(d2/math.cos(math.radians(α))*μs+P/math.pi+dW*μW)
F=2*T/(d2/math.cos(math.radians(α))*μs+P/math.pi+dW*μW)
dW=(2*(d0**3-dh**3))/(3*(d0**2-dh**2))
print(T)
print(F)
print(dW)
梁の曲げ
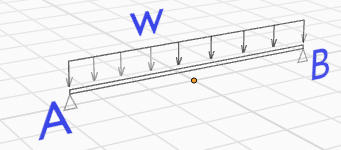
単純支持 分布荷重
$$
M_{\max }=\frac{w l^{2}}{8}
$$
$$
\delta_{\max }=\frac{5 w l^{4}}{384 E I}
$$
paramater_dict= {
'Mmax':['最大曲げ応力','MPa'],
'l':['梁の長さ','mm'],
'w':['分布荷重','N/mm'],
'E':['ヤング率','MPa'],
'I':['断面二次モーメント','mm4'],
'δmax':['最大たわみ量','mm']
}
l = 200
w = 15
E = 200
I = 10000
Mmax=(w*l**2)/8
δmax=(5*w*l**4)/(384*E*I)
print(Mmax)
print(δmax)
輻射伝熱
$$
q=\varepsilon \cdot E_{G} \cdot \sigma A (T_{1}^{4}-T_{2}^{4})
$$
paramater_dict= {
'A':['面積','m2'],
'EG':['形態係数(View Factor)',''],
'T1':['高温側温度','K'],
'T2':['低温側温度','K'],
'q':['伝熱量','W'],
'ε':['輻射率',''],
'σ':['ステファン-ボルツマン係数','W/m2・K4'],
}
A = 1
EG = 1
T1 = 1273
T2 = 273
# q =
ε = 0.9
σ = 5.669*10**-8 #定数
q=ε*EG*σ*A*(T1**4-T2**4)
print(q)
熱衝撃で発生する熱応力(無限板)
急冷の場合です(急冷の場合は最大引っ張り応力が表面になるので、厳しい)
急加熱の場合は内側に最大引っ張り応力が発生するため、下記式より余裕となる。
出展:https://www.jstage.jst.go.jp/article/jsms1963/32/357/32_357_683/_pdf
$$
\sigma=\frac{E \alpha \Delta T}{1-\nu} \cdot \frac{1}{1.5+3.25 / \beta-0.5 \exp (-16 / \beta)}
$$
import math
paramater_dict= {
'E':['ヤング率','MPa'],
'ΔT':['内外温度差','K'],
'α':['線膨張係数','/K'],
'β':['ビオ数',''],
'ν':['ポアソン比',''],
'σ':['熱応力','MPa'],
}
E = 200
ΔT = 10
α = 0.00005
β = 2
ν = 0.3
σ=(E*α*ΔT)/(1-ν)*1/(1.5+3.25/β-0.5*math.exp(-16/β))
print(σ)
ビオ数
$$
\beta=\frac{b h}{k}
$$
paramater_dict= {
'b':['代表長さ(板厚)','m'],
'h':['熱伝達率','W/m2K'],
'k':['熱伝導率','W/mK'],
'β':['ビオ数',''],
}
b = 0.005
h = 500
k = 5
β=(b*h)/(k)
print(β)
伝熱で使用する式
熱解析(CAE)の接触条件
熱解析(CAE)の接触条件(接触熱伝達率)を計算するための式
- 面圧がある場合の接触条件(ボルトで結合している場合等 橘の式です)
keyword : 接触熱抵抗 橘の式 熱接触コンダクタンス 接触熱伝達率
適用に幅があるので注意!(0.5<P<10 MPa)
$$
\mathrm{K}=\frac{1.7 \times 10^{5}}{\frac{\delta_{1}+\delta_{0}}{\lambda_{1}}+\frac{\delta_{2}+\delta_{0}}{\lambda_{2}}} \times \frac{0.6 \mathrm{P}}{\mathrm{H}}+\frac{10^{6} \lambda_{\mathrm{f}}}{\delta_{1}+\delta_{2}}
$$
paramater_dict= {
"K":["接触部の接触熱伝達率","W/m2K"],#この値を接触条件として熱解析へインプット
"δ1":["材料1の表面粗さ","μm"],#Ra :中心線平均粗さ
"δ2":["材料2の表面粗さ","μm"],#Ra :中心線平均粗さ
"λ1":["材料1の熱伝導率","W/mK"],
"λ2":["材料2の熱伝導率","W/mK"],
"λf":["材料間物質の熱伝導率","W/mK"],#空気など
"P":["接触面の押付圧力","MPa"],#ボルト締結による面圧など
"H":["柔らかい方の材料のビッカース硬さ","kg/mm"],#つぶれやすい材料は密着するので熱が伝わります
"δ0":["接触相当長さ(定数)","μm"]
}
δ1 = 32
δ2 = 32
λ1 = 398#銅
λ2 = 398#銅
λf = 0.0241#空気
P = 1
H = 80#銅
δ0=23 #定数です(0.5<P<10MPa)
K = 1.7*10**5/((δ1+δ0)/λ1+(δ2+δ0)/λ2)*0.6*P/H +10**6*λf/(δ1+δ2)
- 隙間の接触熱伝達率
普通の接触熱伝達率を求める式です。
隙間の大きさ次第では自然対流の考慮が必要
$$
hs = \frac{10^{6} \lambda_{\mathrm{f}}}{\delta}
$$
paramater_dict= {
"h":["接触熱伝達率","W/m2K"],
"λf":["隙間を満たす物質の熱伝導率","W/mK"],#空気など
"δ":["接触相当長さ","μm"]
}
λf = 0.0241#空気
δ = 50
h = 10**6*λf/δ