はじめに
Leafletなど、地図を表示するJavaScriptライブラリを用いると簡単に表示できますが、仕組みを理解するためあえて自力で計算してタイルを表示します。
探してみると、計算方法は見つかるのですが、数学が苦手な僕にはちょっと難しい・・・ので、できるだけ分かりやすい式で作りました。
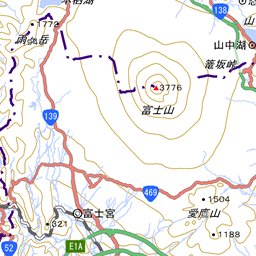
最後に計算結果の確認をするため、富士山山頂の座標(35.36072, 138.72743)をもとに、タイル画像を表示してみます。
参考ページ
国土地理院タイルの特徴
-
タイルはメルカトル図法
-
地図画像は縦横256pixcelの正方形
-
ズームレベル0は全世界を1枚(256×256)で表示する
- 緯度85度まで(256pxに収まる範囲。発散してしまうので)
- 左上を原点とする座標系(西経180度北緯85度)
- 緯度0経度0が画像の中心になる
-
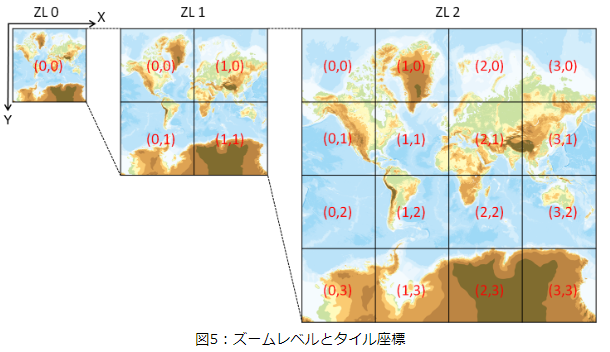
レベル1はそれを縦横2分割(2×2=4枚)、レベル2はさらに2分割(4×4=16枚)
- レベルが上がるごとに詳細な地図に分割されていく(上限は提供される地図毎に異なる)
-
参考画像(国土地理院:地理院タイルについて)
タイルのURL
https://cyberjapandata.gsi.go.jp/xyz/{t}/{z}/{x}/{y}.{ext}
{t}:データID
{x}:左上を原点にしたタイルの位置(X)
{y}:左上を原点にしたタイルの位置(Y)
{z}:ズームレベル
{ext}:拡張子
ex. zoomlevel:6 左上からx方向に57枚目、y方向に23枚目のタイルを取得
https://cyberjapandata.gsi.go.jp/xyz/std/6/57/23.png
-
データID
タイルの種類は地理院タイル一覧参照
タイルの計算方法
経度
レベル0のタイル(地球一周256px)を元に、zoomlevelをかけて算出する
/**
* 経度からX方向の座標情報を計算します
*
* 指定された経度とズームレベルに基づき、以下の4つの値を返します:
* - 世界座標系でのX(0〜1の範囲、グリニッジ子午線が0)
* - ズームレベルを考慮したピクセル単位のグローバルX座標
* - タイルグリッドにおけるX方向のタイル番号(tileNumberX)
* - タイル内(256×256ピクセル)でのX方向ピクセル位置(tileInnerX)
*/
export function calcLatToTileX(lng: number, z: number) {
// 経度(-180〜180)を世界座標系のX(0〜1)に変換
const worldCoordX = (lng + 180) / 360;
// ズームレベル0(256×256px)の座標の位置を計算
let globalPixelX = worldCoordX * 256;
// ズームレベル(2^z)を考慮した座標を計算
globalPixelX = globalPixelX * Math.pow(2, z);
// 1つの画像タイルが256pxなので、256で割って左端からのタイルの枚数(位置)を求める
const tileNumberX = Math.floor(globalPixelX / 256);
// 該当タイル内のピクセル位置を算出する(タイル幅合計を引いた余り)
const tileInnerX = Math.floor(globalPixelX - tileNumberX * 256);
// 計算した値を返す
return {
worldCoordX, // 世界座標(0~1, グリニッジ子午線が原点(0))
globalPixelX, // ズームレベルを考慮したピクセル単位のY座標
tileNumberX, // 該当するタイル番号(0オリジン)
tileInnerX, // タイル内のピクセルY座標(0〜255)
};
}
緯度
- レベル0のタイル(北極~南極が256px)を元に、zoomlevelをかけて算出する
/**
* 緯度からWebメルカトル投影によるY方向の座標情報を計算します。
*
* 指定された緯度とズームレベルに基づき、以下の4つの値を返します:
* - 世界座標系でのY(0〜1の範囲、北極が0)
* - ズームレベルを考慮したピクセル単位のグローバルY座標
* - タイルグリッドにおけるY方向のタイル番号(tileNumberY)
* - タイル内(256×256ピクセル)でのY方向ピクセル位置(tileInnerY)
*
* メルカトル図法で緯度から位置を算出する式 (https://qiita.com/Seo-4d696b75/items/aa6adfbfba404fcd65aa)
* R ln(tan(π/4 + ϕ/2))
* R: 半径
* ϕ: 緯度(ラジアン)
* @param lat - 緯度(-85〜+85度の範囲が推奨)
* @param z - ズームレベル(0以上の整数)
* @returns {{
* worldCoordY: number, // 世界座標系Y(0〜1)
* globalPixelY: number, // ズームレベルを考慮したピクセル単位のY座標
* tileNumberY: number, // Y方向のタイル番号(0オリジン)
* tileInnerY: number // タイル内のピクセルY座標(0〜255)
* }}
*/
export function calcLatToTileY(lat: number, z: number) {
// 緯度からメルカトル図法の座標に変換して、世界座標系のY(0~1)を計算
let worldCoordY = latToWorldY(lat);
// ズームレベル0(256×256px)の座標の位置を計算
let globalPixelY = worldCoordY * 256;
// ズームレベル(2^z)を考慮した座標を計算
globalPixelY = globalPixelY * Math.pow(2, z);
// 1つの画像タイルが256pxなので、256で割って上端からのタイルの枚数(位置)を求める
const tileNumberY = Math.floor(globalPixelY / 256);
// 該当タイル内のピクセル位置を算出する(タイル幅合計を引いた余り)
const tileInnerY = Math.floor(globalPixelY - tileNumberY * 256);
// 計算した値を返す
return {
worldCoordY, // 世界座標(0~1, 北極側が原点(0))
globalPixelY, // ズームレベルを考慮したピクセル単位のY座標
tileNumberY, // 該当するタイル番号(0オリジン)
tileInnerY, // タイル内のピクセルY座標(0〜255)
};
}
/**
* メルカトル図法で投影した位置を元に世界座標系でのY(0〜1、北極が0)を計算する
*
* メルカトル図法の式(半径1の球体を想定)
* ϕ = (π / 180) * 緯度
* y = ln(tan(π/4 + ϕ/2))
* ϕ:緯度(ラジアン)
* y:投影した位置
*
* * 赤道を中心(0)にして、約-85〜+85度の範囲で-π~πの値になる
* * 高緯度では値が急増し無限大になる
* * y = ln((tan(ϕ) + 1) / cos(ϕ)) という式もある(同じ値になる)
*
* 地図で位置を計算するため、北極側が原点(0)で南極側が1となるように正規化した値を返す
*
* @param lat 緯度(-85~85)
* @returns {number} 世界座標系でのY(0〜1、北極が0)
*/
export function latToWorldY(lat: number) {
// 経度をラジアンに変換
const latRad = (Math.PI / 180) * lat;
// 緯度からメルカトル図法の座標に変換する
const mercatorY = Math.log(Math.tan(Math.PI / 4 + latRad / 2));
// -1~1 の範囲になるように調整(-85度~85度の範囲)
let worldCoordY = mercatorY / Math.PI;
// 原点(0)を赤道から、北極へ変換(0~1)
worldCoordY = 1 - (worldCoordY + 1) / 2;
return worldCoordY;
}
上記を元にタイルの位置を求める
- データID(地図の種類): std
- zoomlevel: 10
富士山山頂の座標(35.36072, 138.72743)を入れて計算
| 座標 | タイル | タイル内座標 | |
|---|---|---|---|
| 経度 | 138.72743 | 906 | 154 |
| 緯度 | 35.36072 | 404 | 89 |
計算よりURLは下記の通りとなり、タイル画像には富士山が表示されました