丸い地球を平面で見る
当たり前ですが地球🌏は丸いです。しかし、地球は大きすぎるので場所を調べたり表示するときは縮小された地図を使います。GoogleMapなど普段使う地図は大体平面的なもの多いですが、丸い地球と平らな地図の間には微妙な違いがあり、きちんと理解しておかないと混乱の種になります。ここでは簡単な数学を使ってメルカトル図法を少しわかった気になります。
現在使用されている主要な測地系では地球を回転楕円体として扱いますが、ここでは簡単のため、地球は半径 $\rm{R}=6.3781 \times 10^6 ~\rm{m}$ の完全な球体と仮定して話ます。
[日本測地学会] 地球の形をどのように記載するか
[Wikipedia] 地球半径
特に断りのない限り角度はラジアン表記です
投影法
丸い地球を平らな地図上で表現するためには、地球上の各位置(緯度,経度)を地図上のxy座標に変換する必要があります。座標の変数を次のように定めます。
\left\{
\begin{array}{l}
\mbox{緯度}\ \phi &(-\cfrac{\pi}{2} \le \phi \le \cfrac{\pi}{2})\\
\mbox{経度}\ \lambda &(-\pi \le \lambda \le \pi)\\
\end{array}
\right.

図は [Wikipedia] Stefan Kühn, 投影法 (地図)、地図投影法学習のための地図画像素材集 より引用、一部改変
円筒図法
丸い地球の周りに巻き付けた円筒状のxy平面に投影する手法を円筒図法と呼びます。メルカトル図法は円筒図法の一種です。
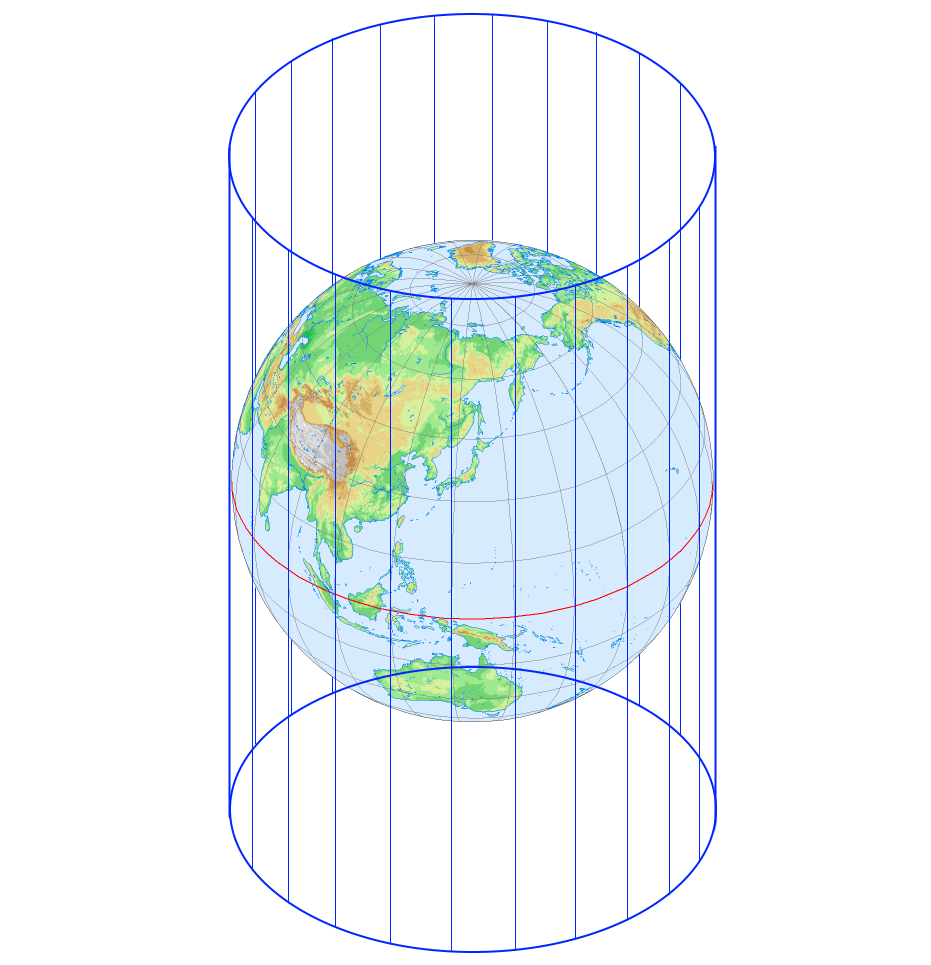
赤道が円筒と接するように配置し、
\left\{
\begin{array}{l}
x = {\rm R}\ \lambda \\
y = f(\phi)
\end{array}
\right.
と緯度経度を投影します。経線はy軸並行な直線に、緯線はx軸平行な直線に投影される特徴があります。
分かりやすい例として心射円筒図法を示します。地球の中心に視点を固定し、「球面上の各点を視線の先の円筒上に写す」と幾何学的に投影すれば、
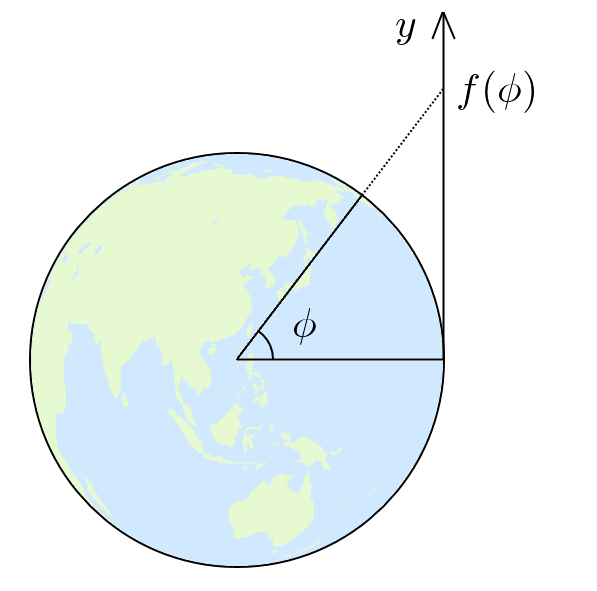
f(\phi) = {\rm R}\ \tan \phi
メルカトル図法ではこのような幾何学的手法ではなく、別の関数 $f(\phi)$ を使います。
f(\phi) = {\rm R}\ \ln \left(\tan \left(\frac{\pi}{4} + \frac{\phi}{2}\right)\right)
何故こんな奇天烈な関数を使うかは等角性を見れば分かります(寧ろ等角性を満たす円筒図法を考えるとこの $f(\phi)$ が導出される、というのが正しい)。
メルカトル図法
メルカトル図法における投影の変換式は、
\left\{
\begin{array}{l}
x = {\rm R}\ \lambda \\
y = {\rm R}\ \ln \left(\tan \left(\cfrac{\pi}{4} + \cfrac{\phi}{2} \right)\right)
\end{array}
\right. \tag{1}
逆変換は、
\left\{
\begin{array}{l}
\lambda = \cfrac{1}{\rm R}\ x \\
\phi = 2\ \arctan \left(\exp (\cfrac{y}{\rm R})\right) - \cfrac{\pi}{2} = {\rm gd}(\cfrac{y}{\rm R})
\end{array}
\right. \tag{2}
緯度 $\phi$ の関数形にはグーデルマン関数 ${\rm gd}(x)$ という名前があるそうです。
[Wikipedia] グーデルマン関数
対称性の確認
緯度方向 $y$ は赤道($ y=\phi=0 $)に対して線対称になります。変換式の形から直感的には分からないので確認します。
f(\phi) = {\rm R}\ \ln \left(\tan \left(\frac{\pi}{4} + \frac{\phi}{2} \right)\right)
と関数を定義して、
\begin{array}{l}
f(\phi) + f(-\phi) &=& {\rm R}\ \ln \left( \tan (\cfrac{\pi}{4} + \cfrac{\phi}{2})\ \tan (\cfrac{\pi}{4} - \cfrac{\phi}{2})\right) \\
&=& {\rm R}\ \ln \left(\cfrac{1 + \tan \cfrac{\phi}{2}}{1 - \tan \cfrac{\phi}{2}}\ \cfrac{1 - \tan \cfrac{\phi}{2}}{1 + \tan \cfrac{\phi}{2}} \right) \\ &=& 0
\end{array}
よって関数 $y=f(\phi)$ は $\phi=0$ に対して線対称です。
地図上の極
変換式によれば $x$ の範囲は $-{\rm R} \pi \le x \le {\rm R} \pi$ ですが、 $y$ は $-\infty \le y \le +\infty$ となります。しかし面積が有限の地図で無限は表現できないため、地図全体が正方形になるように $-{\rm R} \pi \le y \le {\rm R} \pi$ の範囲で切り取るのが通例です。緯度に換算すると
\begin{array}{l}
{\rm max}\ |\phi| &=& {\rm gd}(\pi) \\
&=& 2\ \arctan \left( {\rm e}^\pi\right) - \cfrac{\pi}{2} \\
&=& 1.4844 \ldots \tag{3}
\end{array}
地図上での緯度・経度の微小変化量
微分します。
\begin{array}{l}
\cfrac{\partial \lambda}{\partial x} = \cfrac{1}{\rm R}\\
\cfrac{\partial \phi}{\partial y} = \cfrac{\cos \phi}{\rm R}\\
\cfrac{\partial \phi}{\partial x} = \cfrac{\partial \lambda}{\partial y} = 0
\end{array} \tag{4}
緯線上の長さ $\Delta x = |x_1 - x_2|$ に対する経度は、
\Delta \lambda = \frac{1}{\rm R}~\Delta x = \frac{|x_1 - x_2|}{\rm R}
経線上の長さ $\Delta y$ に対する緯度は、
\Delta \phi = \frac{\cos \phi}{\rm R}~\Delta y
注意として、緯度の変化量 $\Delta \phi$ は 緯度 $\phi$ に依存するので $\Delta y$ が微小量でしか成り立ちません。微小量でない $\Delta y= y_2 - y_1$ の場合は積分して、
\Delta \phi = \displaystyle{\int_{y_1}^{y_2}\frac{\cos \phi}{\rm R}~dy}
$\cos \phi$ を $y$ で表す必要があるので、式(1)より
\begin{array}{l}
\exp(\cfrac{y}{\rm R}) &=& \tan \left(\cfrac{\pi}{4} + \cfrac{\phi}{2}\right) \\
&=& \cfrac{1 + \sin \phi}{\cos \phi}
\end{array}
$\sin^2\phi + \cos^2\phi = 1$ に代入して、
\begin{array}{l}
\left( \exp(2\cfrac{y}{\rm R}) + 1 \right)~ \cos^2\phi - 2\exp(\cfrac{y}{\rm R})~ \cos \phi = 0\\
\cos \phi = \cfrac{1}{\cosh\cfrac{y}{\rm R}}\ \ (|\phi| \ne \cfrac{\pi}{2})
\end{array} \tag{5}
求める値は、
\begin{array}{l}
\Delta \phi &=& \displaystyle{\int_{y_1}^{y_2}\cfrac{dy}{{\rm R}~\cosh \cfrac{y}{\rm R}}} \\
&=& \left[ 2\arctan\left(\exp(\cfrac{y}{\rm R})\right) \right]_{y_1}^{y_2}\\
&=& {\rm gd}(\cfrac{y_2}{\rm R}) - {\rm gd}(\cfrac{y_1}{\rm R})
\end{array}
確かに式(2)でも出てきたグーデルマン関数の形になります。$y_1 \rightarrow -\infty,\ y_2 \rightarrow +\infty$ と極限をとると、地球全体($-\frac{\pi}{2} \le \phi \le \frac{\pi}{2}$)に対応する $\Delta\phi = \pi$ になります。
等角性
メルカトル図法の大きな特徴のひとつです。投影前の球面上での角と、投影後の地図上での角が等しいことを意味しています。ここで、曲面における曲線(もしくは直線)のなす角度とは、その曲線の接ベクトルが挟む角度になります。
直交する緯線と経線
例として緯線と経線で示します。3次元空間における球面上の点 $\vec{p}$ は、
\vec{p} = \left(
\begin{array}{c}
{\rm R} \cos\phi \ \cos\lambda \\
{\rm R} \cos\phi \ \sin\lambda \\
{\rm R} \sin\phi
\end{array}
\right)
と表現できます。緯度 $\phi$ を固定して経度 $\lambda$ を動かすと緯線になるので、緯線の接ベクトルは、
\frac{\mathrm{d} \vec{p}_\lambda }{\mathrm{d}\lambda} =
\left(
\begin{array}{c}
-{\rm R} \cos\phi \ \sin\lambda \\
{\rm R} \cos\phi \ \cos\lambda \\
0
\end{array}
\right)
反対に経度 $\lambda$ を定数と見て緯度 $\phi$ でパラメータ表示したのが経線だから、その接ベクトルは、
\frac{\mathrm{d} \vec{p}_\phi }{\mathrm{d}\phi} =
\left(
\begin{array}{c}
-{\rm R} \sin\phi \ \cos\lambda \\
-{\rm R} \sin\phi \ \sin\lambda \\
{\rm R} \cos\phi
\end{array}
\right)
ふたつの接ベクトルの内積を計算すると
\frac{\mathrm{d} \vec{p}_\lambda }{\mathrm{d}\lambda} \cdot \frac{\mathrm{d} \vec{p}_\phi }{\mathrm{d}\phi} = 0
より球面上のすべて緯線と経線は直交しているのが分かります。また、投影後の地図上でも緯線はx軸平行・経線はy軸平行で、確かに緯線と経線がなす角 $90^\circ$ は保存されています。
一般の角
では緯線・経線以外の角はどうでしょうか?まず図のように球面上の点 $(\phi,\lambda)$ における接平面を考えます(球面は全微分可能でそのような接平面が存在します)。さきほど示した緯線・経線の接ベクトルを大きさ1に揃えたものを $\vec{u}, \vec{v}$ とすれば、接平面は $\vec{u}$ と $\vec{v}$ によって張られる平面となります。また、$\vec{u}$ と $\vec{v}$ は直交するので、接平面上に正規直交座標uvを考えることができます。
普段我々が直感的に角や形を認識する平面と同じ正規直交系であり、球面上の微小領域における角や形はこのuv平面で考えられます。
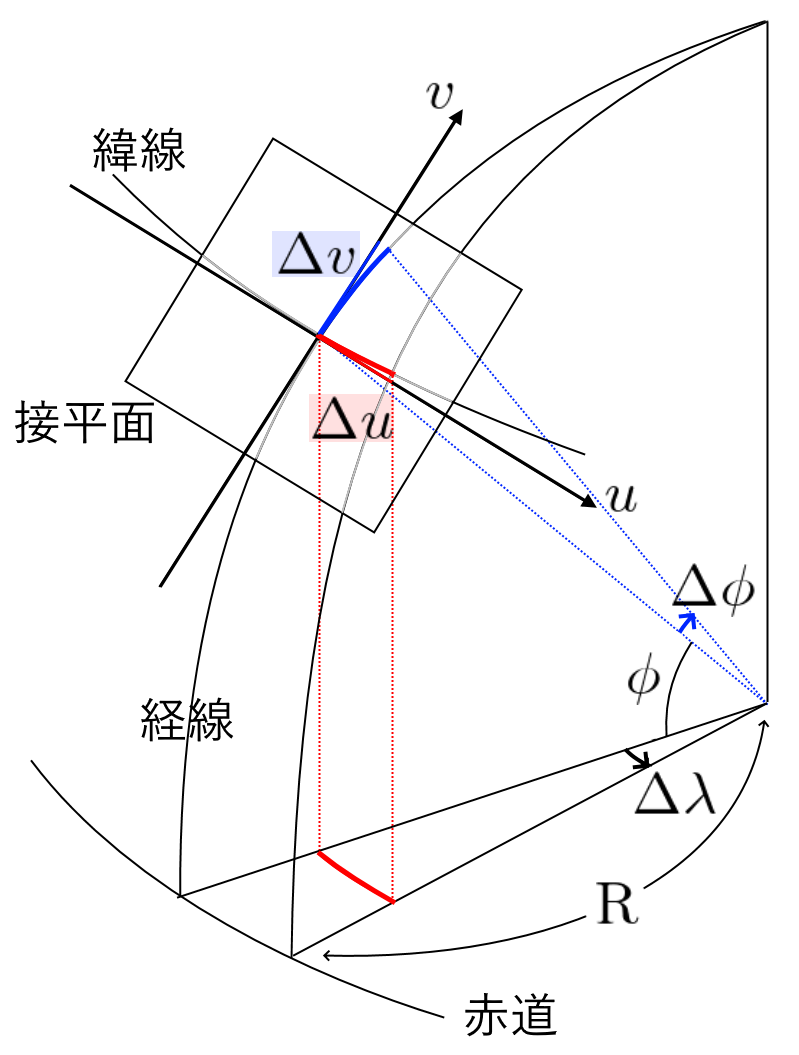
このuv平面での微小量が地図上のxy平面に投影される様子を調べます。写像で表記してみると、
\left( \begin{array}{c}
\mathrm{d}u \\ \mathrm{d}v
\end{array} \right)
\stackrel{f_1}{\longmapsto}
\left( \begin{array}{c}
\mathrm{d}\phi \\ \mathrm{d}\lambda
\end{array} \right)
\stackrel{f_2}{\longmapsto}
\left( \begin{array}{c}
\mathrm{d}x \\ \mathrm{d}y
\end{array} \right)
写像 $f_1, f_2$ を表す変換行列を計算します。$f_2$ の方は式(4)より、
F_2 = \left( \begin{array}{cc}
\cfrac{\partial x}{\partial \phi} & \cfrac{\partial x}{\partial \lambda} \\
\cfrac{\partial y}{\partial \phi} & \cfrac{\partial y}{\partial \lambda}
\end{array} \right) = \left( \begin{array}{cc}
0 & {\rm R} \\
\cfrac{\rm R}{\cos\phi} & 0
\end{array} \right)
$f_1$ の方は図で考えます。各微小量の関係は、
\left\{
\begin{array}{l}
\Delta u = {\rm R} \cos\phi \ \Delta \lambda \\
\Delta v = {\rm R} ~ \Delta \phi
\end{array}
\right.
微分形で表すと、
\begin{array}{l}
\cfrac{\partial\lambda}{\partial u} = \cfrac{1}{{\rm R}\cos\phi} \\
\cfrac{\partial\phi}{\partial v} = \cfrac{1}{\rm R}
\end{array}
これ以外の変数の間には関係がないので、
\frac{\partial\phi}{\partial u}=\frac{\partial\lambda}{\partial v}=0
よって求める$F_1$は、
F_1 = \left( \begin{array}{cc}
\cfrac{\partial\phi}{\partial u} & \cfrac{\partial\phi}{\partial v} \\
\cfrac{\partial\lambda}{\partial u} & \cfrac{\partial\lambda}{\partial v}
\end{array} \right) = \left( \begin{array}{cc}
0 & \cfrac{1}{\rm R} \\
\cfrac{1}{{\rm R}\cos\phi} & 0
\end{array} \right)
したがって、uv平面からxy平面への写像 $f_3$ は合成 $f_2 \circ f_1$ となり(行列乗算の順番に注意)その変換行列は、
\begin{array}{l}
\left( \begin{array}{c}
\mathrm{d}u \\ \mathrm{d}v
\end{array} \right)
\stackrel{f_3}{\longmapsto}
\left( \begin{array}{c}
\mathrm{d}x \\ \mathrm{d}y
\end{array} \right) \\
F_3 = F_2 F_1 = \cfrac{1}{\cos\phi}\left( \begin{array}{cc}
1 & 0 \\
0 & 1
\end{array} \right)
\end{array}
$F_3$ は単位行列のスカラー倍であるから、この行列が表す変換は $\dfrac{1}{\cos\phi}$ 倍の拡大で角は不変と言えます。つまりメルカトル図法では、局所的に見た形状は投影前後で比 $1:\dfrac{1}{\cos\phi}$ の相似になっています。
注意として角は保存されますが、面積は保存されず $\dfrac{1}{\cos^2\phi}$ 倍になります。高緯度ほど面積が誇張して表示されるので、メルカトル図法におけるグリーンランドの面積は印象ほど大きくない話は有名です。図のように同じ面積を表す赤い丸を描画すると、等角性より各円形に歪みはありませんが地図上で表示される面積は高緯度ほど大きくなります。
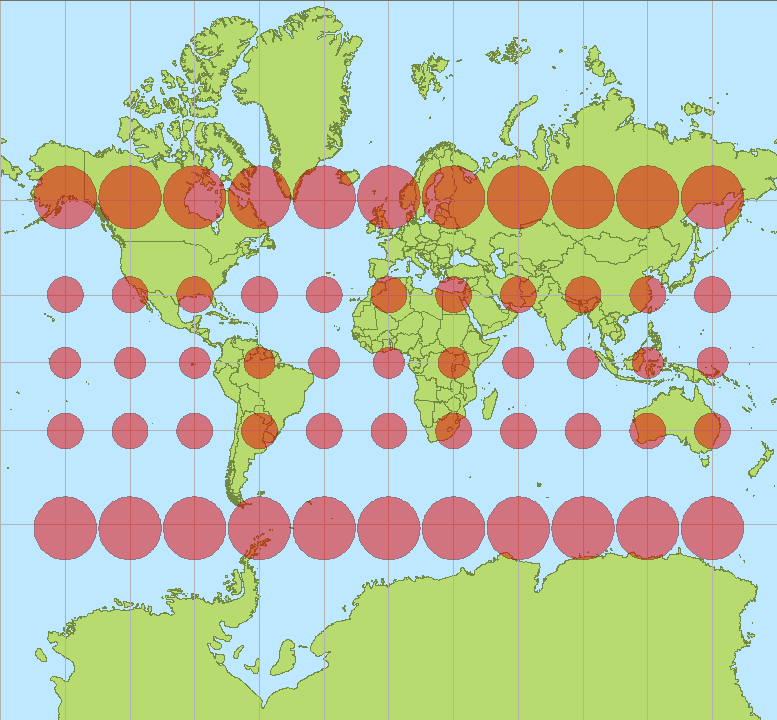
図は [Wikipedia] Stefan Kühn, メルカトル図法 より引用
地球上の直線
一般に曲面上の直線は測地線として定義されます。直感的には2点を結ぶ曲線のうち最短距離となるものに該当します。球面においては、測地線は大円(球の中心を通る平面との交円)になります。
xy平面上に投影した直線
大円は球の中心を通る平面との交円になるので、中心から $(\phi_0,\lambda_0)$ を結ぶ方向を平面の法ベクトルとして
\vec{n} = \left(
\begin{array}{c}
{\rm R}\ \cos\phi_0 \ \cos\lambda_0 \\
{\rm R}\ \cos\phi_0 \ \sin\lambda_0 \\
{\rm R}\ \sin\phi_0
\end{array}
\right)
求める大円上の点 $(\phi,\lambda)$ が満たす条件は、
\begin{array}{l}
\vec{p} = \left(
\begin{array}{c}
{\rm R}\ \cos\phi \ \cos\lambda \\
{\rm R}\ \cos\phi \ \sin\lambda \\
{\rm R}\ \sin\phi
\end{array}
\right) \\
\vec{p} \cdot \vec{n} = 0 \tag{6}
\end{array}
式(5)より $|\phi| \ne \cfrac{\pi}{2}$ の下で、
\begin{array}{l}
\cos\phi = \cfrac{1}{\cosh\cfrac{y}{\rm R}} \\
\sin\phi = \tanh\cfrac{y}{\rm R}
\end{array}
式(3)で示した通り、$|\phi| = \dfrac{\pi}{2}$ はxy平面には現れないので気にせず進みます。式(6)に代入して、
\begin{array}{l}
\cos\phi_0~\cos\lambda_0\cfrac{\cos\cfrac{x}{\rm R}}{\cosh\cfrac{y}{\rm R}} + \cos\phi_0~\sin\lambda_0\cfrac{\sin\cfrac{x}{\rm R}}{\cosh\cfrac{y}{\rm R}} + \sin\phi_0~\tanh\cfrac{y}{\rm R} = 0 \\
\cos\phi_0 \left( \cos\lambda_0~\cos\cfrac{x}{\rm R} + \sin\lambda_0~\sin\cfrac{x}{\rm R} \right) + \sin\phi_0~ \sinh\cfrac{y}{\rm R} = 0 \\
\cos\phi_0 \cos\left( \cfrac{x}{\rm R} - \lambda_0 \right) + \sin\phi_0~ \sinh\cfrac{y}{\rm R} = 0 \tag{7} \\
\end{array}
$\phi_0 \ne 0$の場合は式(7)の両辺を$\sin\phi_0$で割って、
\cfrac{1}{\tan\phi_0} \cos\left(\dfrac{x}{\rm R} - \lambda_0\right) + \sinh\cfrac{y}{\rm R} = 0
ここで $A(x) = \dfrac{1}{\tan\phi_0} \cos\left(\dfrac{x}{\rm R} - \lambda_0\right)$ とおいて、 ${\rm e}^{y/{\rm R}}$ の二次方程式を解くと、
\begin{array}{l}
A(x) + \sinh\cfrac{y}{\rm R} = 0 \\
\exp(2\cfrac{y}{\rm R}) + 2~A(x)~\exp(\cfrac{y}{\rm R})- 1 = 0 \\
y = {\rm R}~\ln\left(-A+\sqrt{A^2+1}\right) \tag{8}
\end{array}
$\phi_0 = 0$ の場合は式(7)に代入して、
\begin{array}{l}
\cos\left(\cfrac{x}{\rm R} - \lambda_0\right) = 0 \\
| \cfrac{x}{\rm R} -\lambda_0 | = \cfrac{\pi}{2} + n \pi \ \ (n = 0,1) \\
\end{array}
y軸平行な直線となり、これは経線に該当します。
$|\phi_0| = \pi/2$ の場合は式(7)に代入して、
\begin{array}{l}
\sinh\cfrac{y}{\rm R} = 0 \\
y = 0
\end{array}
これは赤道に該当します。
東西方向の直線
例として東京 $(\phi_{\rm t},\lambda_{\rm t}) = (35.681367,139.766798)$ (緯度・経度の値はオイラー角)から東西方向に直線を引いてみます。法ベクトル $(\pi/2 - \phi_{\rm t}, \lambda_{\rm t} - \pi)$ に対する大円が目的の直線だから式(8)に代入して
\begin{array}{l}
A(x) &=& \cfrac{1}{\tan(\cfrac{\pi}{2} - \phi_{\rm t})}\ \cos\left( \cfrac{x}{\rm R} - \lambda_{\rm t} + \pi \right) \\
&=& -\tan\phi_{\rm t}\ \cos\left( \cfrac{x}{\rm R} - \lambda_{\rm t}\right) \\
y &=& {\rm R}\ \ln\left( - A + \sqrt{A^2 + 1} \right) \\
&=& {\rm R}\ \ln\left( \tan\phi_{\rm t}\ \cos\left( \cfrac{x}{\rm R} - \lambda_{\rm t}\right) + \sqrt{\tan^2\phi_{\rm t}\ \cos^2\left( \cfrac{x}{\rm R} - \lambda_{\rm t}\right) + 1} \right)
\end{array}
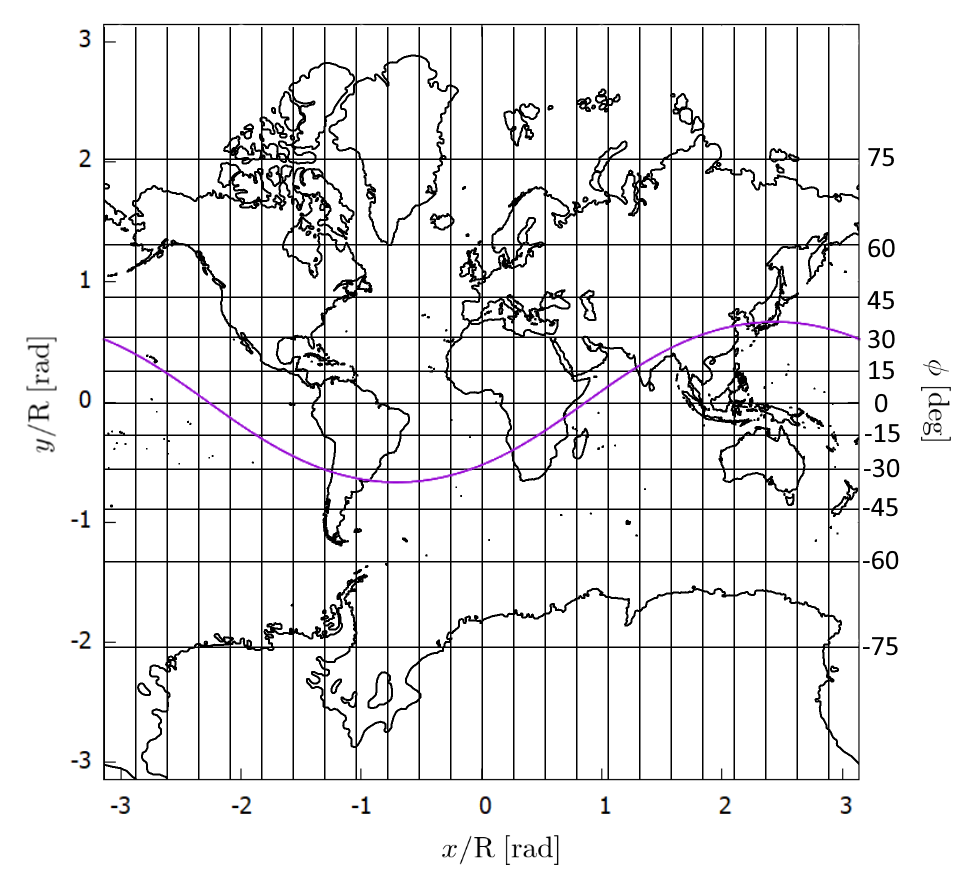
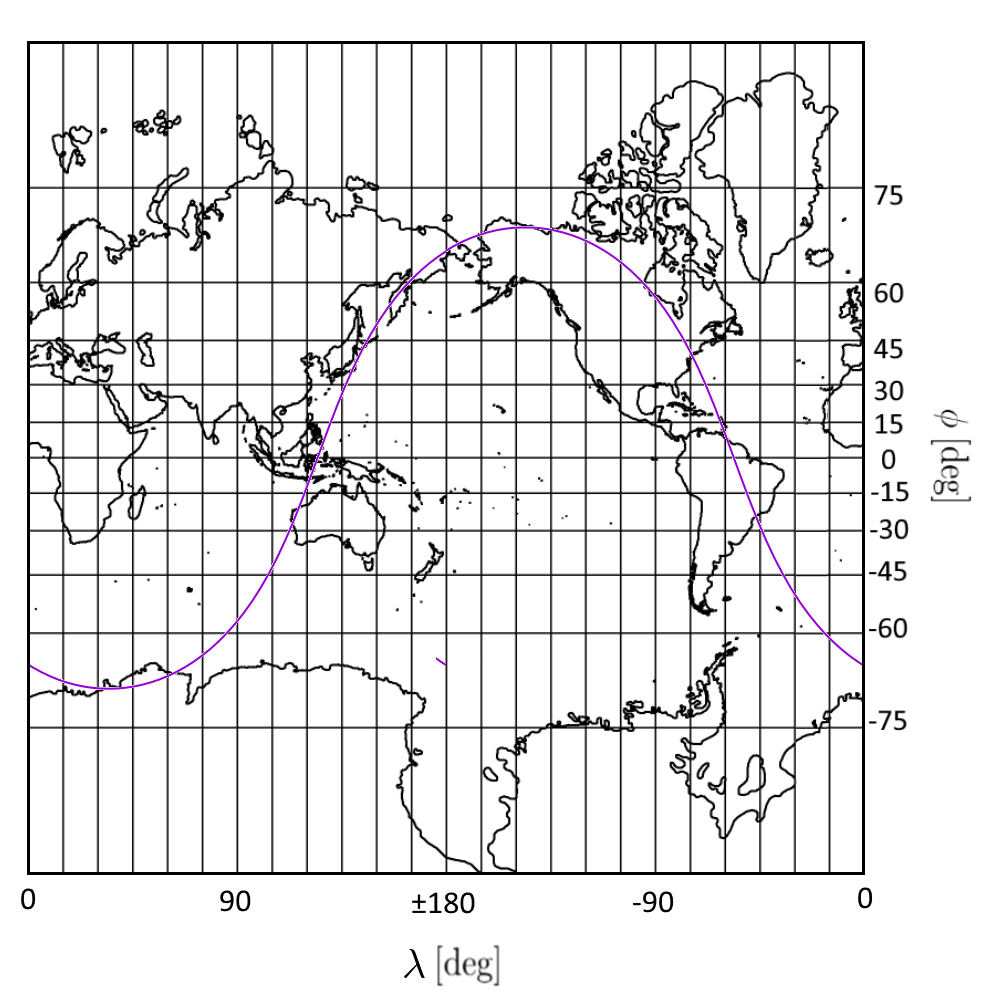
gnuplot で描画すると図のようになります。
gnuplot> set xrange [-pi:pi]
gnuplot> set yrange [-pi:pi]
gnuplot> set size square
gnuplot> phi0 = (90 - 35.681367) * pi / 180
gnuplot> lambda0 = (180 - 139.766798) * pi / 180
gnuplot> A(x) = 1 / tan(phi0) * cos(x-lambda0)
gnuplot> y(x) = log(-A(x) + sqrt(A(x)**2 + 1))
gnuplot> plot y(x) with lines lw 2
2点間の最短距離
球面の測地線は大圏コースとも呼ばれ、2点間を最短距離で結ぶコースであることが知られています。航空機の航路などもこの大圏コースをとる場合が多く、日本からアメリカ本土を目指す飛行機はハワイ上空を通らない、という話が有名です。例として東京 $(\phi_1,\lambda_1) = (35.681367,139.766798)$ とニューヨーク $(\phi_2,\lambda_2) = (40.748424, -73.985664)$ (緯度・経度の値はオイラー角)を結ぶ大圏コースを計算します。
まず目的の大円をつくる平面の法ベクトル $\vec{n}$ を求めますが、これは3次元空間の外積で簡単に表現できます。大きさをすべて1に揃えると便利なので正規化して計算して、
\begin{array}{l}
\cfrac{\vec{p_1}}{\rm R} =\left(
\begin{array}{c}
\cos\phi_1 \ \cos\lambda_1 \\
\cos\phi_1 \ \sin\lambda_1 \\
\sin\phi_1
\end{array}
\right), \ \
\cfrac{\vec{p_2}}{\rm R} = \left(
\begin{array}{c}
\cos\phi_2 \ \cos\lambda_2 \\
\cos\phi_2 \ \sin\lambda_2 \\
\sin\phi_2
\end{array}
\right) \\
\cfrac{\vec{n}}{\rm R} = \left(
\begin{array}{c}
\cos\phi_0 \ \cos\lambda_0 \\
\cos\phi_0 \ \sin\lambda_0 \\
\sin\phi_0
\end{array}
\right) = \cfrac{\vec{p_1} }{\rm R}\times \cfrac{\vec{p_2}}{\rm R}
\end{array}
具体的に計算して、
\frac{\vec{p_1} }{\rm R}\times \frac{\vec{p_2}}{\rm R}
= \left( \begin{array}{c}
0.767\ldots \\ 0.527\ldots \\ 0.342\ldots
\end{array} \right)
= \left( \begin{array}{c}
x_0 \\ y_0 \\ z_0
\end{array} \right)
$ \cos\lambda_0 > 0 , \sin\lambda_0 > 0$ より $ 0 < \lambda_0 < \dfrac{\pi}{2}$ に注意して、
\begin{array}{l}
\phi_0 = \arcsin z_0 = 19.99\ldots \ {\rm deg} \\
\lambda_0 = \arctan\left(\cfrac{y_0}{x_0}\right) = 34.47\ldots \ {\rm deg}
\end{array}
式(8)に代入してプロットすると図のようになります。大圏コースは図示した大円の短い方の弧に該当し、アラスカあたりの上空を通ることが分かります。
本投稿に掲載されたすべての図表は「CC 表示-継承 3.0」の下、配布されています。
[Qiita利用規約] 第7条(投稿内容の著作権)