目的
現在、Deeplearningの応用研究を大学で行なっています。実際に前処理やモデル構築などをしていく中で基礎的な知識を同時並行でおさらいしたいという思いがありchainerやDeeplearningについての基礎的知識をアウトプットしていきます!!
今回はパーセプトロン、ニューラルネット、活性化関数についてです!!
パーセプトロンについて
まず簡単に今後活性化関数を説明していく上でも重要となるパーセプトロン(単層パーセプトロン)についてザッと説明していきます。
パーセプトロンとは以下の式のように表すことができる入出力を持つアルゴリズムです。
a = b + w1 * x1 + w2 * x2
a が0以下なら y = 0
a が0より大きければ y = 1(この状態をよく発火という)
x:入力
w:重み
b:バイアス
y:出力
パーセプトロンは重みとバイアスを調整を調整することによってAND演算やOR演算を実装することができ2層のパーセプトロンならXOR演算(非線形領域)も実装できます。
活性化関数とは
活性化関数とは入力を出力に変換する関数(どのように発火するかを決める関数)です。
a = b + w1 * x1 + w2 * x2
y = h(a)
式で表すと上記のh()にあたる部分が 活性化関数です。
ステップ関数
パーセプトロンにおいては出力が0か1になる「ステップ関数」が活性化関数として使用されます。
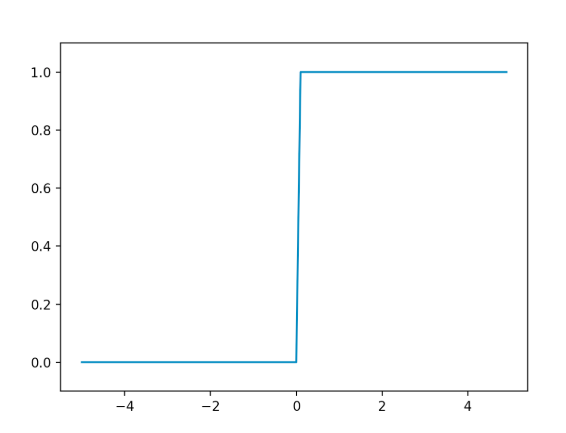
このステップ関数以外の活性化関数を使用することでニューラルネットワークを構築することができます。
シグモイド関数
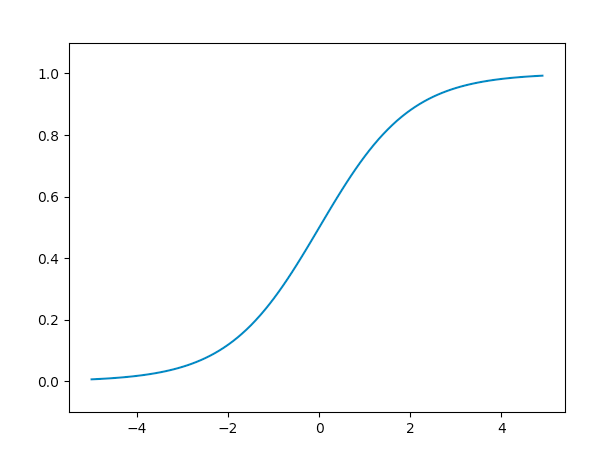
シグモイド関数はニューラルネットワークでよく用いられる活性化関数です。
h(x) = 1/(1+exp(-x))
上記の式で表すことができます。
非線形関数
グラフを見てもわかるようにパーセプトロンは0か1の二値、ニューラルネットは連続的な実数値が流れていることがわかると思います。
共通点としては重要な入力値でなければ小さい値(0に近い)、重要であれば大きな値(1に近い)を返すこと。また、お互い非線形関数であることです。
ニューラルネットでは活性化関数は非線形関数を用いなくてはなりません。
これは線形関数を用いると層を深くすることができなくなり、単層のパーセプトロンと同等のものになってしまうからです。
以下に式でその様子を示します。
h(x) = cx を活性化関数とする。
この場合、この活性化関数は線形ですね。
ではこれに層を加えた出力を見てみましょう。
y = h(h(h(x)))
= c * c * c * x
= c3 * x
a = c3 とすると
y = a * x
結局、線形の関数になってしまうのです。
このことから層を深くするニューラルネットでは活性化関数に非線形関数を用いる必要があります。
まとめ
活性化関数とは入力を出力に変換する関数ということが分かりました。
その中でも線形なものと非線形なものがあり、ニューラルネットでは出力を非線形にすることで層を深くし、より精度の高い結果を出力することが可能になります。
これからも基礎的な事項についてまとめていきますね!!