ランダム・フォレスト分析の基礎まとめ
1. ランダムフォレストの概要
決定木のアンサンブルと見なされます。
アンサンブル学習は「弱いアルゴリズム」を組み合わせてより頑健な「強いアルゴリズム」を構築します。
強いアルゴリズムには汎化誤差が改善され、過学習に陥りにくい。
2. 関連用語
2-1. バギング
データの一部を使って学習し、それを何度も繰り返して最後に合わせる方法。
並列処理が可能。
2-2. ブースティング
データの一部を抽出してそれで弱学習機を作り、最後に合わせるのはバギングと同様。弱学習器を1つずつ順番に構築していく手法で、前回の結果を利用する。
なので計算を並列化できず学習に時間がかかる。
ブースティングでは,各ステップごとに弱学習器を構築して損失関数を最小化する。
その際に,各学習データの扱いはずっと平等ではなく、各学習データのうち,前のステップで間違って識別されたものへのウェイトを重くして,次のステップで間違ったものをうまく識別できるようにしていく。
2-2-1. アダブースト
前回の結果で誤分類された値の重みを大きくするように更新する。ブースティングと単に言えばこれを指すことが多いらしい。
2-2-2. 勾配ブースティング
勾配ブースティングでは,各ステップのパラメータ最適化の際に,勾配降下法を用いている。勾配を求めて学習していく,という形をとるので,損失関数をパラメータ行列で微分してあげるのを繰り返して,所定回数に達したら終了。
2-2-3. GBDT(Gradient Boosting Decision Tree)
弱学習機に決定木を使った勾配ブースティングのこと。
過学習の制御がパラメータ決定の中心になっている。
shrinkage
各ステップの学習が後続ステップの学習に影響を及ぼしてしまうため,個々のステップの影響を下げて学習速度をゆっくりにするパラメータ。
shrinkageのパラメータνは0<ν<1の値を取る。
(xgboostだと,このパラメータはetaで表され,デフォルトは0.3)。
ある程度小さいほうが,過学習が抑制されて精度が上がります.
決定木の制御パラメータ
個々の弱学習器である,決定木自体の表現力を制御するパラメータとして
- 木の深さ(xgboostだとmax_depth)
- 葉の重みの下限(同じくmin_child_weight)
- 葉の追加による損失減少の下限(gamma)
といったものがあります.深さが浅いほど,また下限が大きいほど,当然単純な木になりやすいので過学習の抑制に働きます。
データの割合パラメータ
各ステップで決定木の構築に用いるデータの割合というパラメータもあります。
学習データから非復元抽出したサブサンプルを用いることで,確率的勾配降下法(Stochastic Gradient Descent: SGD)に近い効果が得られます。
これも過学習抑制で精度向上につながります。
2-3. ブートストラップ
1つの標本から復元抽出を繰り返して大量の標本を生成し、それらの標本から推定値 を計算し、母集団の性質やモデルの推測の誤差などを分析する方法。
復元抽出:重複を許したデータ抽出
3. アンサンブル学習(集団学習)
学習器の性能は汎化能力(未学習データに対する予測能力)で評価します。
汎化能力を向上させるためには
• 単一の学習器の性能を向上させる方法
• 個々に学習した複数の学習器を何らかの形で融合させて汎化能力を向上させる方法
の二つが考えられます。
3−1. アンサンブル学習の分類
アンサンブルする学習器の複雑さという基準
(i)複雑な学習器を独立に学習し、それらをアンサンブルする形態
(ii)単純な学習器を逐次的に学習し、それらをアンサンブルする形態
アンサンブル学習器の種類
(a)同じ学習器で学習した結果をアンサンブルする形態
(b)異なる学習器で学習した結果をアンサンブルする形態
の二つの観点がある。
- バギング、ランダムフォレストは(i)(a)
- ブースティングは(ii)(a)
となる。
4. なぜRandomForestは精度が高くなるのか?
RandomForestを含む決定木のような弱学習器は集団学習に向いている。
これはバイアスーバリアンスの観点から説明できます。
バイアスーバリアンス理論によると汎化誤差は次のように分解されます。
汎化誤差 = バイアス + バリアンス + ノイズ
ここでバイアスは モデルの表現力 に由来する誤差、
バリアンスは データセットの選び方 に由来する誤差、
ノイズは 本質的に減らせない誤差 です。
決定木はアルゴリズムの性質上、モデルが学習データからうける影響が大きくバリアンスが高い学習モデルです。RandomForestやbaggingなどの集団学習アルゴリズムは バリアンスを低減させることで 精度を向上を図ります。
一方、SVMであまり集団学習の話を聞かないのは、SVMが 低バリアンス のモデルだから。
5. ランダムフォレストのアルゴリズム
-
大きな n 個の ブートストラップ標本 を復元抽出する。
トレーニングデータセットから n 個のサンプルをランダムに選択。 -
ブートストラップ標本から決定木を成長させる。各ノードで以下の作業を行う。
- d 個の特徴量をランダムに 非復元抽出する。
- 例えば情報利得を最大化することにより、目的関数に従って最適な分割となる特徴量を使ってノードを分割する。
-
ステップ 1,2 をk 回繰り返す。
決定木ごとの予測をまとめて「多数決」に基づいてクラスタラベルを割り当てる。
6. sklearn モジュールで ランダムフォレスト
6-1. 実装例
RandomForestClassifierの呼び出し例
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000, n_features=4,
n_informative=2, n_redundant=0,
random_state=0, shuffle=False)
clf = RandomForestClassifier(max_depth=2, random_state=0)
clf.fit(X, y)
print(clf.feature_importances_)
[ 0.17287856 0.80608704 0.01884792 0.00218648]
print(clf.predict([[0, 0, 0, 0]]))
[1]
6-2. ブートストラップ標本
RandomForestClassifier 実装を初めとするほとんどの実装では、ブートストラップ標本のサイズは、元のトレーニングデータセットのサンプル個数と等しくなるように選択される。
→それにより通常はバイアスとバリアンスが適切に調整される。
6-3. 説明変数
学習用データから、学習させて生成した RandomForestモデル における説明変数の重要度(係数)は、上記例のように
feature_importances_
属性で出力できます。
RandomForestClassifier オブジェクトの主な属性一覧
| 属性 | 説明 |
|---|---|
| estimators_ | The collection of fitted sub-estimators. |
| classes_ | クラスラベルの配列 |
| n_classes_ | 分類したクラス数 |
| n_features_ | 特徴数 |
| n_outputs_ | 出力数 |
| feature_importances_ | 重要度(係数)の配列 |
| oob_score_ | out-of-bag 推定値を用いて得られたトレーニングデータセットのスコア。 |
7. ランダムフォレストによる分類可視化例
決定木の分類結果を可視化する関数の実装。
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
#setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
# 最小値, 最大値からエリアの領域を割り出す
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# resolutionの間隔で区切った領域を定義
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
# print(xx1.shape)
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot all samples
X_test, y_test = X[test_idx, :], y[test_idx]
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
# highlight test samples
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0], X_test[:, 1], c='',
alpha=1.0, linewidth=1, marker='o',
s=55, label='test set')
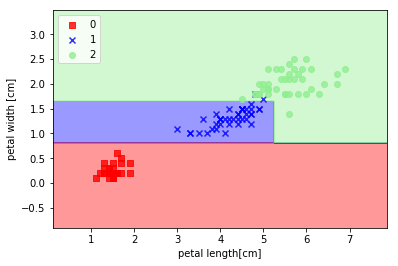
irisデータで DecisionTreeClassifier を利用した分類例。
エントロピーを指標とする決定木のインスタンスを生成して、最大階層3で分類実行しています。
from sklearn.tree import DecisionTreeClassifier
from sklearn.cross_validation import train_test_split
# データを読み込み
from sklearn.datasets import load_iris
iris = load_iris()
# 説明変数 (それぞれ、がく片や花弁の幅、長さを示します)
# irisのデータセットの第3, 4カラム
x = iris.data[:, [2, 3]]
# 目的変数 (0, 1, 2 がそれぞれの品種を表します)
# irisのそれぞれのデータごとのラベル
y = iris.target
# データセットを訓練データとテストデータに分割
# 今はtest_size=0.3なので訓練データ7割テストデータ3割にしている
# sklearn.model_selection.train_test_split
# http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
x_combined = np.vstack((x_train, x_test))
y_combined = np.hstack((y_train, y_test))
# エントロピーを指標とする決定木のインスタンスを生成
tree = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=0)
tree.fit(x_train, y_train)
plot_decision_regions(x_train, y_train, classifier=tree)
plt.xlabel('petal length[cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.show()
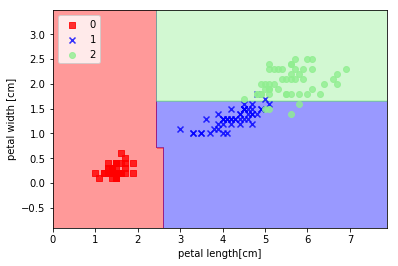
次はirisデータで RandomForestClassifier を利用した分類例。
エントロピーを指標とするランダムフォレストのインスタンスを生成して、10個の決定木からアンサンブル学習を実行しています。
from sklearn.ensemble import RandomForestClassifier
# エントロピーを指標とするランダムフォレストのインスタンス生成
forest = RandomForestClassifier(criterion='entropy',
n_estimators=10, random_state=1, n_jobs=2)
# n_jobs=2 -> CPU コアを2つ使用して並列処理
# n_estimators=10 -> 10個の決定木からランダムフォレストをトレーニング
#
# ランダムフォレストのモデルにトレーニングデータを適合させる
forest.fit(x_train, y_train)
plot_decision_regions(x_combined, y_combined, classifier=forest)
plt.xlabel('petal length[cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.show()
8. xgboostのパラメータ
| 属性 | 説明 |
|---|---|
| max_depth | 木の深さ |
| min_child_weight | 葉の重みの下限 |
| gamma | 葉の追加による損失減少の下限 |
| colsample_bytree | 各ステップの決定木ごとに用いる特徴量をサンプリングする。ランダムフォレストで行われているのと同じで,特徴量同士の交互作用を考慮した形のモデリングができるという利点があります。 |
| nrounds | 木の本数。当然木の本数が多いほうが結果も安定するし精度も上がりますが,その一方で学習に時間がかかってしまいます。 |
ブースティングはパラメータの推定時に前ステップの結果を用いるため、各ステップの推定を同時に行うことができません。
そのためステップ数が増えること(=木の本数が増えること)は,計算時間の増加を招きます。
呼び出しサンプルと初期値
from xgboost import XGBClassifier
classifier = XGBClassifier()
classifier.fit(X_train, y_train)
# XGBClassifier(base_score=0.5, booster='gbtree', #colsample_bylevel=1,
# colsample_bytree=1, gamma=0, learning_rate=0.1, #max_delta_step=0,
# max_depth=3, min_child_weight=1, missing=None, #n_estimators=100,
# n_jobs=1, nthread=None, objective='binary:logistic', #random_state=0,
# reg_alpha=0, reg_lambda=1, scale_pos_weight=1, #seed=None,
# silent=True, subsample=1)
参考資料
- アンサンブル学習
https://www.slideshare.net/holidayworking/ss-11948523 - 回帰モデルの比較 - ARMA vs. Random Forest Regression
http://qiita.com/TomokIshii/items/b3ebe2b60c5d3d5a0d5a - Rとブートストラップ
http://www1.doshisha.ac.jp/~mjin/R/Chap_44/44.html - sklearn.ensemble.RandomForestClassifier
http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html