(追記)
本記事後半部,Random Rorest Regression に関する訂正記事を投稿しました.こちらも参照ください.時系列データ分析の処理でやってはいけないこと(反省を含めて)
Pythonで時系列データ分析を行う場合,統計モデリングのStatsModelsが備えるTimes series analysis (tsa) モジュールを使うのが第1の選択肢になると考えられる.また,機械学習ライブラリ Scikit-learn には別のコンセプトで回帰を行う,決定木回帰(Decision Tree Regression)やRandom Forest Regressionがあるので,これも試してみたいと考え,比較検討した.
(プログラミング環境:Python 2.7.11, Pandas 0.18.0, StatsModels 0.6.1, Scikit-learn 0.17.1 になります.)
伝統的な自己回帰モデルのグループ
時系列データ分析の文献を開くと多くの場合,次の順番で説明が出てくる.
| 略称 | 説明 |
|---|---|
| AR | 自己回帰(Auto Regression)モデル |
| MA | 移動平均(Moving Average)モデル |
| ARMA | 自己回帰移動平均モデル |
| ARIMA | 自己回帰和分移動平均モデル |
各モデルの詳細はWikipedia等を参照していただくとして,基本的にARMAは,AR , MAを含有するモデルであり, ARIMA は,ARMA を含むモデルなので,ライブラリとしては ARIMA がサポートされていれば,上記4つのモデルはすべて対応可能となる.但し,StatsModelsではAPIとしてAR, ARMA, ARIMA が用意されている.
今回,分析を行うデータとして,"Nile" を取り上げた.
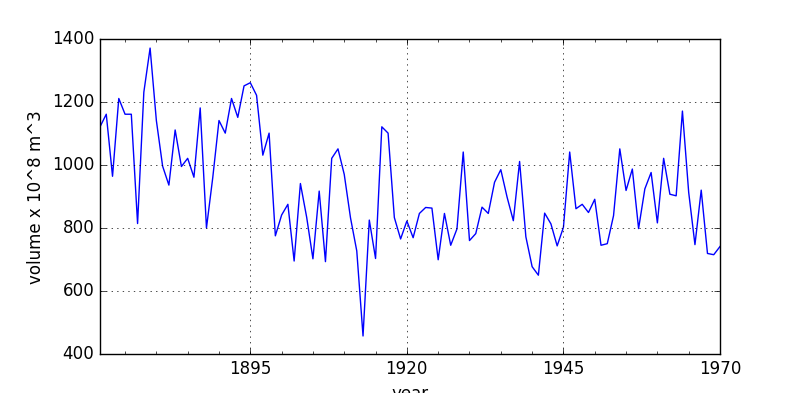
Nile River flows at Ashwan 1871-1970
This dataset contains measurements on the annual flow of the Nile as measured at Ashwan for 100 years from 1871-1970. There is an apparent changepoint near 1898.
アフリカ,ナイル川流量の各年ごとのデータで,StatsModelライブラリ内に用意されているサンプルデータである.
自己回帰モデルでは多くの場合「定常性」がモデル適用の前提条件になっているが,上のプロットでは単調増加,単調減少の様子が見られないので,ARMAモデルを当てはめることにする.
ARMAモデルの次数選択
およそ100年間の時系列データとなっているので,フィット用(訓練用)のデータとして前半70年分,モデルテスト用のデータとして後半30年分を割り当てることとする.ARMAモデルの次数(p, q)を選ぶ必要があるが,まずコレログラムとも呼ばれるACFプロット(Autocorrelation function plot), PACFプロット(Partial autocorrelation plot)を作図してみる.
def load_data():
df_read = sm.datasets.nile.load_pandas().data
s_date = pd.Series(
[pd.to_datetime(str(int(y_str))) for y_str in df_read['year']]
)
df = df_read.set_index(s_date)
df = df.drop('year', axis=1)
return df
df_nile = load_data()
# Plot Time Series Data
ax = df_nile['volume'].plot(figsize=(8,4), grid=True)
ax.set_xlabel('year')
ax.set_ylabel('volume x 10^8 m^3')
plt.show()
# Data Split (70: 30)
# ACF, PACF
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_train.values, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_train.values, lags=40, ax=ax2)
Fig. ACF and PACF plot of "Nile" data
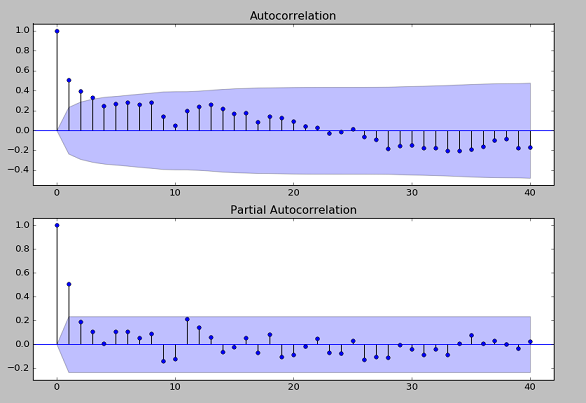
ARMA(p, q) で,ACFプロット(上)より q=[0, 1, 2, 3] が選択肢に入り,PACFプロット(下)より p = [0, 1] が選択肢に入ることが(なんとなく)分かる.一応,ARMA(p=1, q=3) を視野に入れつつ次数選択のユーティリティで情報を出力させると以下のようになった.
info_criteria = sm.tsa.stattools.arma_order_select_ic(
df_train.values, ic=['aic', 'bic']
)
print(info_criteria.aic_min_order)
print(info_criteria.bic_min_order)
ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
"Check mle_retvals", ConvergenceWarning)
>>> (1, 1)
>>> (1, 0)
収束性に関するWarningが出ていることに注意.Warningをふまえた上で,AIC(モデル選択基準値)からはARMA(1, 1), BIC(モデル選択基準値)からはAMMA(1, 0) が良さそうとの情報を得た.よってこの2つのモデルをデータにフィットさせてみる.
arma_10 = sm.tsa.ARMA(df_train, (1, 0)).fit()
arma_11 = sm.tsa.ARMA(df_train, (1, 1)).fit()
これは,特にError, Warningもなく処理された.戻り値 arma_10, arma_11 はフィット後のモデル・オブジェクト(ARMAResultsクラス)である.一応,より高次のモデルARMA(1, 2), ARMA(1, 3) も試してみた.
arma_12 = sm.tsa.ARMA(df_train, (1, 2)).fit()
arma_13 = sm.tsa.ARMA(df_train, (1, 3)).fit()
(中略,Traceback 情報など.)
ValueError: The computed initial AR coefficients are not stationary
You should induce stationarity, choose a different model order, or you can
pass your own start_params.
上のようなValueErrorが発生した.(エラーメッセージは,定常性(stationary)について言及していますが...)パラメータ算定時における収束性に問題がありARMA(1, 2),ARMA(1, 3)への当てはめは難しい状況である.この先,この原因を深く追及してもいいが,今回は,ARMA vs. Random Forest Regressor がテーマであるので,フィットができたARMA(1, 0)とARMA(1, 1) を用いて検討を進める.
ARMAモデルの検証
まず,AICの値を確認する.
print('ARMA(1,0): AIC = %.2f' % arma_10.aic)
print('ARMA(1,1): AIC = %.2f' % arma_11.aic)
>>> ARMA(1,0): AIC = 910.94
>>> ARMA(1,1): AIC = 908.92
AIC値は,ARMA(1, 1)モデルの方が小さい.
次に訓練データ区間(70年分)のモデル推定値とその後のテスト区間(30年)のモデル推定値を算出する.
# in-sample predict
arma_10_inpred = arma_10.predict(start='1871-01-01', end='1940-01-01')
arma_11_inpred = arma_11.predict(start='1871-01-01', end='1940-01-01')
# out-of-sample predict
arma_10_outpred = arma_10.predict(start='1941-01-01', end='1970-01-01')
arma_11_outpred = arma_11.predict(start='1941-01-01', end='1970-01-01')
AICの算定,推定値の算出ともにARMAモデル結果クラス(ARMAResultsクラス)のメソッドで求めることができるような実装となっている.元データの値,推定値をまとめてプロットする.
# plot data and predicted values
def plot_ARMA_results(origdata, pred10in, pred10out, pred11in, pred11out):
px = origdata.index
py1 = origdata.values
plt.plot(px, py1, 'b:', label='orig data')
px_in = pred10in.index
plt.plot(px_in, pred10in.values, 'g')
plt.plot(px_in, pred11in.values, 'c')
px_out = pred10out.index
plt.plot(px_out, pred10out.values, 'g', label='ARMA(1,0)')
plt.plot(px_out, pred11out.values, 'c', label='ARMA(1,1)')
plt.legend()
plt.grid(True)
plt.show()
plot_ARMA_results(df_nile, arma_10_inpred, arma_10_outpred,
arma_11_inpred, arma_11_outpred)
Fig. Nile data - original data and ARMA estimated data
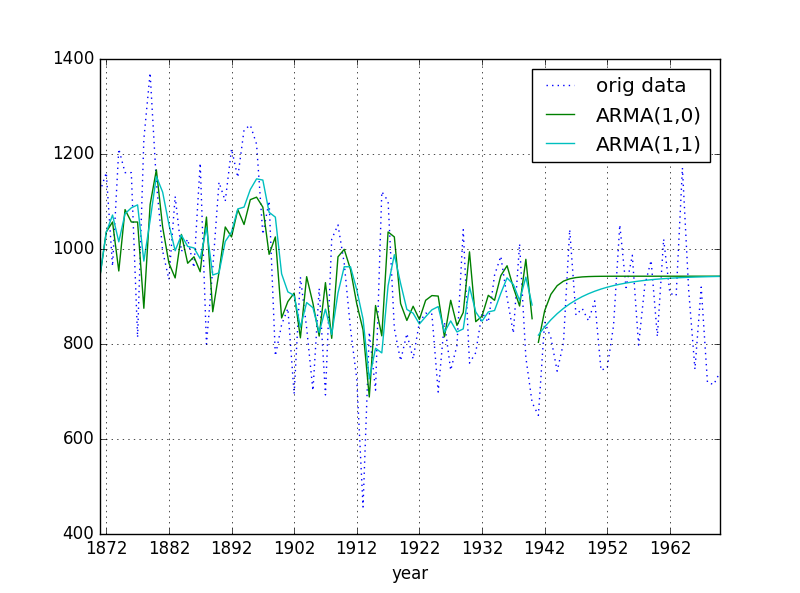
1870年から1940年までが訓練区間 (in-sample),それ以降がテスト区間(out-of-sample)である.少し分かりにくいが,なんとなくARMA(1,1)の方が,実データに近いように見える.後でモデル比較のため,残差からMSE(Mean Squared Error)を求めておく.
# Residue (mse for train)
arma_10_mse_tr = np.array([r ** 2 for r in arma_10.resid]).mean()
arma_11_mse_tr = np.array([r ** 2 for r in arma_11.resid]).mean()
# Residue (mse for test)
arma_10_mse_te = np.array([(df_test.values[i] - arma_10_outpred[i]) **2
for i in range(30)]).mean()
arma_11_mse_te = np.array([(df_test.values[i] - arma_11_outpred[i]) **2
for i in range(30)]).mean()
Random Forest 回帰
Random Forest回帰のベースとなっているのは,決定木回帰(Decision Tree Regression)である.決定木のアルゴリズム自体,大雑把でも理解しておく必要があると思われるが,本記事では説明を省略し,Scikit-learnの機能をブラックボックスとして扱うことにする.Scikit-learnのドキュメントにはExampleがあるが,それを試した結果が下図である.
Fig. Decision Tree Regression Example
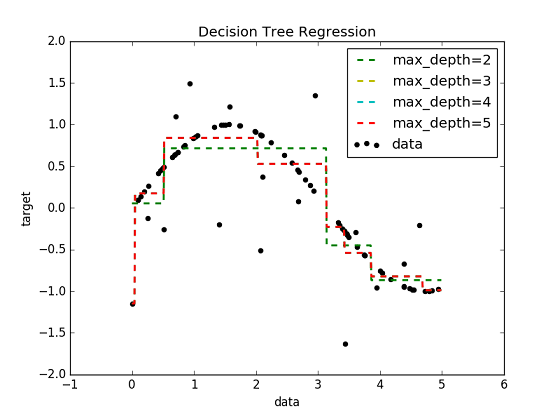
階段状の直線でフィットすることが特徴となっている.今回は単変量の時系列データであるが,いくつかの過去のデータ使って現在の値を推定するモデルとしてみた.具体的には,
Volume_current ~ Volume_Lag1 + Volume_Lag2 + Volume_Lag3
というモデルである.訓練データとテストデータを前回と同じ(70, 30)にしたかったが,Lag値を計算する過程でNaNがでるので,初めの部分をdropna()して,(67, 30) のデータ長とした.
まず,データの前処理を行う.
df_nile['lag1'] = df_nile['volume'].shift(1)
df_nile['lag2'] = df_nile['volume'].shift(2)
df_nile['lag3'] = df_nile['volume'].shift(3)
df_nile = df_nile.dropna()
X_train = df_nile[['lag1', 'lag2', 'lag3']][:67].values
X_test = df_nile[['lag1', 'lag2', 'lag3']][67:].values
y_train = df_nile['volume'][:67].values
y_test = df_nile['volume'][67:].values
Scikit-learnのRandomForestRegressorを使用.
from sklearn.ensemble import RandomForestRegressor
r_forest = RandomForestRegressor(
n_estimators=100,
criterion='mse',
random_state=1,
n_jobs=-1
)
r_forest.fit(X_train, y_train)
y_train_pred = r_forest.predict(X_train)
y_test_pred = r_forest.predict(X_test)
推定値は,下図のようになった.
Fig. Nile data - original data and Random Forest Regression results
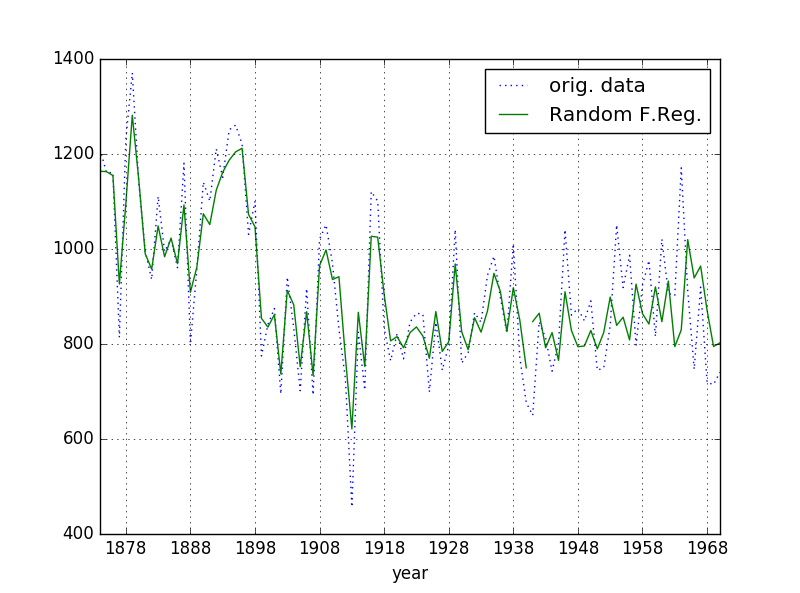
最後にMSEを算定する.
# check residue (mse)
train_resid = y_train - y_train_pred
RFR_mse_train = np.array([r ** 2 for r in train_resid]).mean()
test_resid = y_test - y_test_pred
RFR_mse_test = np.array([r ** 2 for r in test_resid]).mean()
モデル精度比較
各モデルのMSE(Mean Squared Error)を比較する.
| Model | MSE of in-samle (train) | MSE of out-of-sample (test) |
|---|---|---|
| ARMA(1,0) | 24111.0 | 18684.4 |
| ARMA(1,1) | 22757.3 | 16625.8 |
| Random F. Regressor | 3470.1 | 15400.3 |
(MSE : smaller ... better)
次数の異なるARMAモデル同士の比較では,ARMA(1,1) の方が訓練区間,テスト区間ともMSEが小さく精度が良いことが分かるが,これは前に求めたAICの値の比較と整合性がある.
ARMAモデルとRandom Forest回帰モデルの比較では,訓練区間では大きな差をつけてRandom Forest回帰のMSEが小さい値となっている.またテスト区間でもRandom Forest回帰が小さいが,差は約7%である.精度的にはRandom Forest回帰が有利であるが,統計モデルを当てはめたARMAモデルでは,予測中央値の他,信頼区間(例えば95%信頼区間)の情報も得られるという点を考慮すべきと思われる.用途に応じて使い分けたい.
(ARMAとRandom Forest回帰のプロット図を見比べてみると,ラインの様子が大きく異なることに改めて驚かされました.また,どのモデルも十分なパラメータ調整ができていない可能性がある点にご注意ください.)
参考文献 (web site)
- StatsModels Documentation
http://statsmodels.sourceforge.net/stable/index.html - Scikit-learn Documentation
http://scikit-learn.org/stable/ - 現場ですぐ使える時系列データ分析(横内大介 (著), 青木義充 (著))
http://www.amazon.co.jp/ebook/dp/B00KNRL068/ - Python Machine Learning - O'reilly media (By Sebastian Raschka)
http://shop.oreilly.com/product/9781783555130.do