はじめに
今回も始まりました。やってみよう分析!シリーズ
Excelを使うと様々な分析をすることが可能であることを見てきました。まだ紹介していないExcelの機能として、__VBA(Visual Basic for Applications)__と呼ばれるプログラミング言語が搭載されています。VBAを駆使することでExcel上の処理を自動化することができます。例えば、毎週定形レポートを提出するタスクがあるならば、そのレポートを自動生成するマクロを作ると作業効率が格段に上がります。
VBAは事務的な処理だけではなく、簡単な数値計算も実行することが可能です。ここでは数値計算の例として __Q-learning__と呼ばれる強化学習のシミュレーション実装例を紹介します。またQ-learningの行動選択手法として __ε-greedy__と __Softmax__と呼ばれる2つを紹介します。
参考文献
この記事では下記の書籍を参考にしました。理論的背景よりも実装例にフォーカスしています。非常に易しく書かれているので強化学習を専門的に学んだことがない方でも理解しやすいと思います。
- ロボットインテリジェンス―進化計算と強化学習 (図解ロボット技術入門シリーズ), 伊藤 一之, オーム社 (2007/04)
途中の解説で出てくるSoftmax行動選択については下記が参考になります。
- Bandit Algorithms for Website Optimization, John Myles White, Oreilly & Associates Inc; 1版 (2012/12/31)
またSoftmax行動選択では __逆関数法__を使って行動を選択します。逆関数法については下記の資料にわかりやすい解説があります。
- 第7回 確率不等式と擬似乱数(第5章), 講義ノート, 確率と統計 O, 杉山将
強化学習の一般的な解説としては下記2つが参考になります。
-
強化学習, Richard S.Sutton, Andrew G.Barto(著), 三上 貞芳, 皆川 雅章(共訳), 森北出版 (2000/12)
-
強くなるロボティック・ゲームプレイヤーの作り方 ~実践で学ぶ強化学習~, 八谷 大岳, 杉山 将, マイナビ (2008/8/27)
強化学習
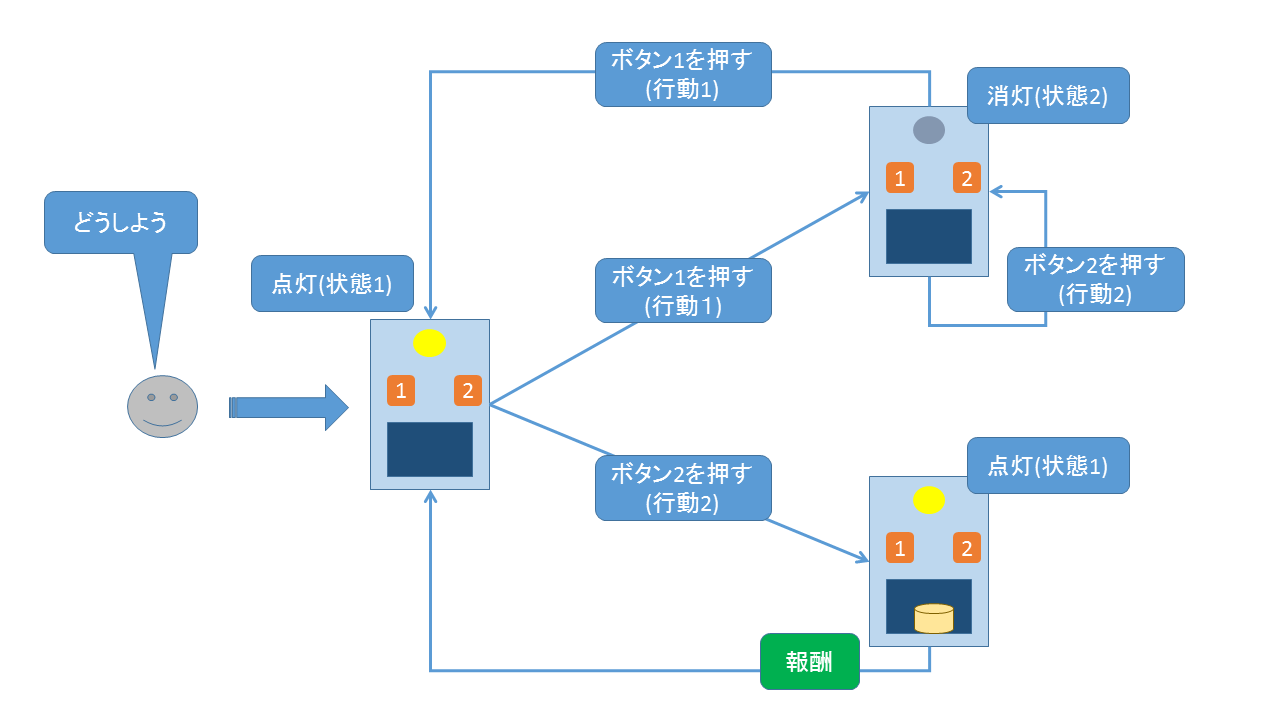
本記事では上記1番目の文献で紹介されているチーズ製造機を例に強化学習を考えてみます。このチーズ製造機は電源状態を表す電球と2つのボタンがついています。ボタン1(電源)を押す( 行動1)と電源が入り電球が点灯( 状態1)、その状態からボタン2を押す( 行動2)とチーズが生成します。電源が入った状態1からまたボタン1を押すと電球が消灯します( 状態2)。初期状態は電源が付いている状態(状態1)としましょう。
このような性質を持つチーズ製造機から効率よくチーズを生成する行動をロボット( エージェント)に学習させることを考えます。学習の流れは下記のような図になります。このフローから学習すべき行動は状態1の時にボタン2を押し、状態2の時にはボタン1を押す事だとわかります。
Q-learning
__Q-learning__と呼ばれる学習手法でチーズ製造機の行動を学習させることを考えてみます。Q-learning(Q学習)では、まず状態 $s$ と行動 $a$ のある関数 $Q(s, a)$ によって行動の報酬への貢献度を評価します。$Q(s,a)$ の更新式は下記のように与えられます。
Q(s, a) \leftarrow (1-\alpha)Q(s, a) + \alpha \Bigl\{ r(s, a) + \gamma \max_{a'} Q(s', a') \Bigr\}
ここで $\alpha$ は学習率($0 < \alpha \leq 1 $)、$\gamma$ は割引率($0 \leq \gamma < 1$)、$r(s,a)$ は状態 $s$ において行動 $a$ を実行した時に獲得される報酬。$s'$ は状態 $s$ において行動 $a$ を実行した結果遷移した状態。$\max_{a'}Q(s',a')$ は状態 $s'$ において行動 $a'=1 \text{ or } a'=2$ を探索した最大の $Q(s',a')$ を表しています。
$Q$値が求められた後、以下で説明する行動選択手法で各状態において $Q(s, a)$ が最大になるような行動が選択されます。$Q$値の評価と行動の選択を繰り返すことで最適な行動の学習が進行します。
行動選択
計算された $Q$値に対して行動を選択する方法として、ここでは __ε-greedy__と __Softmax__を紹介します。2つとも確率的に行動を選択していきます。
ε-greedy
この手法ではある小さい確率 $\epsilon$ で行動1、行動2をランダムに選択。確率 $1 - \epsilon $ で最大の $Q(s,a)$ を与えている行動を選択します。例えば $\epsilon = 0.1$ なら 高い確率($1 - \epsilon = 0.9$) で最大の$Q$値を与えている行動を選択し、小さい確率でランダムに行動を選択します。つまり不適切な行動も非常に小さい確率ですがトライすることになります。
Softmax
Softmax手法ではある状態 $s$ に対して次のSoftmax関数を$Q(s,a)$ を使って次のように定義します($T$ は温度)。
\frac{e^{Q(s,a) / T}}{\sum_{a}e^{Q(s,a) / T}}
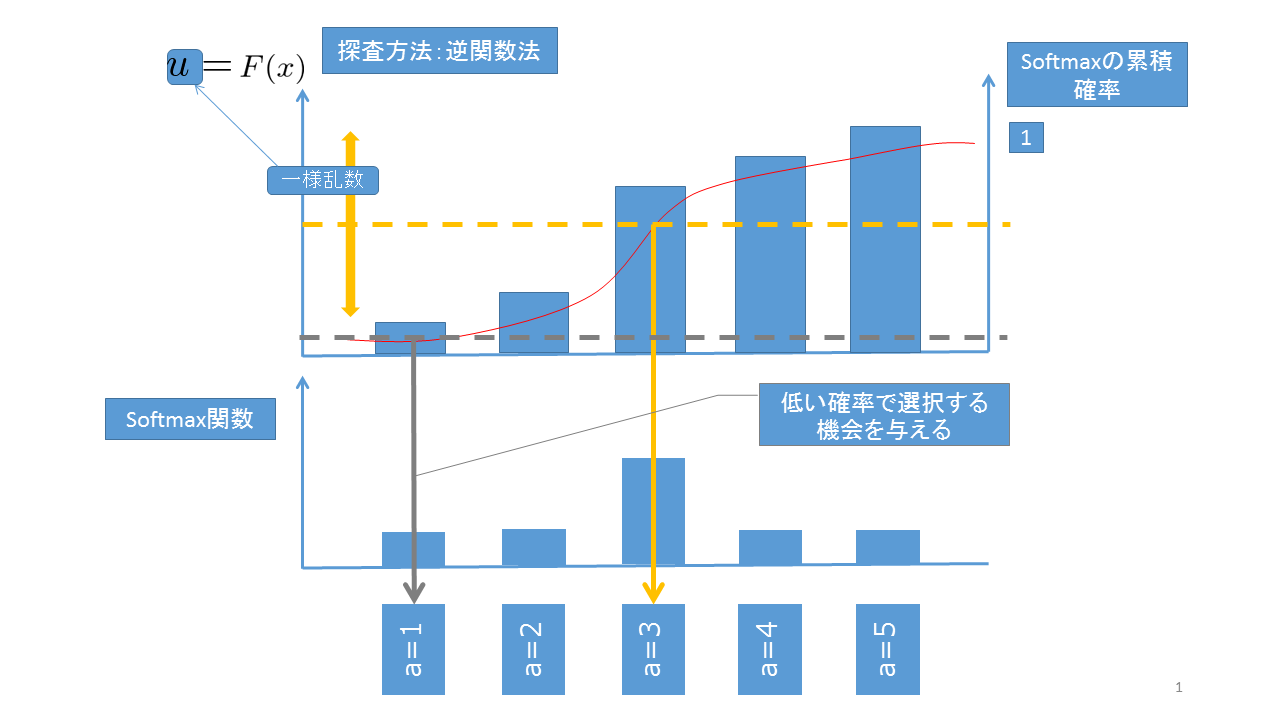
これを選択すべき行動に対する確率分布だとみなして、例えば逆関数法で行動を選択します。$Q$値が大きくなれば自然とその行動のSoxtmax関数の値も大きくなり、その行動が選択されやすくなります。
Q-learning実装例
以下にQ-learningのVBAによる実装例を示します(行動選択はε-greedyとSoftmax)。下記コードを実行するためにはVBAエディタにコードを貼り付けマクロを実行します(事前に開発タブがExcelに出ている状態にします。ココらへんを参照に設定します。)。温度、割引率、学習率の各種パラメータを変えると出力される結果も異なってきます。
'状態sにおける最大のQの値を取得
Function maxQval(s As Integer, numA As Integer, Qtable As Worksheet) As Double
Dim max As Double
Dim i As Integer
max = Application.WorksheetFunction.max(Qtable.Rows(s))
maxQval = max
End Function
'行動選択
Function selectAction(s As Integer, numA As Integer, Qtable As Worksheet) As Integer
Dim max As Integer
Dim i As Integer
Dim numIMax As Integer
Dim iMax() As Integer
ReDim iMax(numA)
numIMax = 1
iMax(numIMax) = 1
max = Qtable.Cells(s, 1)
'配列に最大値のインデックスを代入。
For i = 2 To numA Step 1
If Qtable.Cells(s, i) > max Then
max = Qtable.Cells(s, i)
numIMax = 1
iMax(numIMax) = i
ElseIf Qtable.Cells(s, i) = max Then
numIMax = numIMax + 1
iMax(numIMax) = i
End If
Next i
'count>1のときは配列の要素をランダムで選ぶ。
selectAction = iMax(Int(Rnd * numIMax + 1))
End Function
'epsilonGreedyによる行動選択
Function epsilonGreedy(epsilon As Double, numA As Integer, s As Integer, Qtable As Worksheet) As Integer
Dim x As Integer
If Rnd < epsilon Then
x = Int(Rnd * numA + 1)
Else
x = selectAction(s, numA, Qtable)
End If
epsilonGreedy = x
End Function
'softMaxに使うボルツマンウェイト
Function boltzmannWeight(s As Integer, numA As Integer, t As Double, Qtable As Worksheet) As Double()
Dim z() As Double
ReDim z(numA)
Dim Qsum As Double
Qsum = 0
For i = 1 To numA Step 1
Qsum = Qsum + Math.Exp(Qtable.Cells(s, i) / t)
Next i
For i = 1 To numA Step 1
z(i - 1) = Math.Exp(Qtable.Cells(s, i) / t) / Qsum
Next i
boltzmannWeight = z
End Function
'softMaxによる行動選択
Function softMax(t As Double, numA As Integer, s As Integer, Qtable As Worksheet) As Integer
Dim cumProb As Double
cumProb = 0
Dim index As Integer
Dim x() As Double
ReDim x(numA)
Dim i As Integer
i = 0
x = boltzmannWeight(s, numA, t, Qtable)
'逆関数法で行動のインデックスを取得
For j = 1 To numA Step 1
cumProb = cumProb + x(j - 1)
i = j
If cumProb > Rnd Then
Exit For
End If
Next j
softMax = i
End Function
'メイン
Sub Qlearning()
'a=1:電源スイッチを押す, a=2:チーズ製造ボタンを押す
's=1:電源ON(ライトが点灯), s=2:電源OFF(ライトが消灯)
Dim numA As Integer '行動の数
Dim numS As Integer '状態の数
Dim Qtable As Worksheet
Dim a As Integer '行動
Dim s As Integer '状態
Dim sd As Integer '遷移後の状態
Dim reward As Integer '報酬
Dim qMax As Double 'Q値の最大値
Dim trialMax As Integer '試行回数
Dim stepMax As Integer '1試行あたりの最大の行動回数
Dim alpha As Double '学習率
Dim gamma As Double '割引率
Dim epsilon As Double 'ランダム行動選択の確率
Dim net As Integer '報酬額
Dim t As Double '温度パラメータ
Dim flag As Integer '行動選択手法の選択のためのフラグ
'初期値
numA = 2
numS = 2
alpha = 0.3
gamma = 0.5
epsilon = 0.1
trialMax = 10000
stepMax = 10
net = 10
s = 1
t = 10
flag = 0
Set Qtable = Worksheets("Sheet1")
'セルに初期値を代入
Qtable.Cells(1, 1) = 0
Qtable.Cells(1, 2) = 0
Qtable.Cells(2, 1) = 0
Qtable.Cells(2, 2) = 0
Randomize 'ランダム数の初期化
Dim i, j As Integer
flag = Application.InputBox("choose a selection rule/ 1: epsilonGreedy, 2: softMax", "Selection Rule", "", Type:=1)
If flag = False Then
MsgBox "最初から"
Exit Sub
End If
For i = 1 To trialMax Step 1
For j = 1 To stepMax Step 1
'行動選択
Select Case flag
Case 1
a = epsilonGreedy(epsilon, numA, s, Qtable) 'ε-greedy(f=0)
Case 2
a = softMax(t, numA, s, Qtable) 'ソフトマックス(f=1)
Case Else
MsgBox "最初から"
Exit Sub
End Select
'報酬の付与
reward = 0
If a = 1 Then
If s = 1 Then
sd = 2
Else
sd = 1
End If
Else
sd = s
If s = 1 Then
reward = net
End If
End If
'Qの更新
qMax = maxQval(sd, numA, Qtable)
Qtable.Cells(s, a) = (1 - alpha) * Qtable.Cells(s, a) + alpha * (reward + gamma * qMax)
If reward > 0 Then
s = 1
Exit For '成功したら初期状態へ戻って再試行
Else
s = sd '続行
End If
Next j
Next i
End Sub
実行結果
表示タブからマクロを起動してQlearningを実行します(VBAエディタから実行しても構いません)。
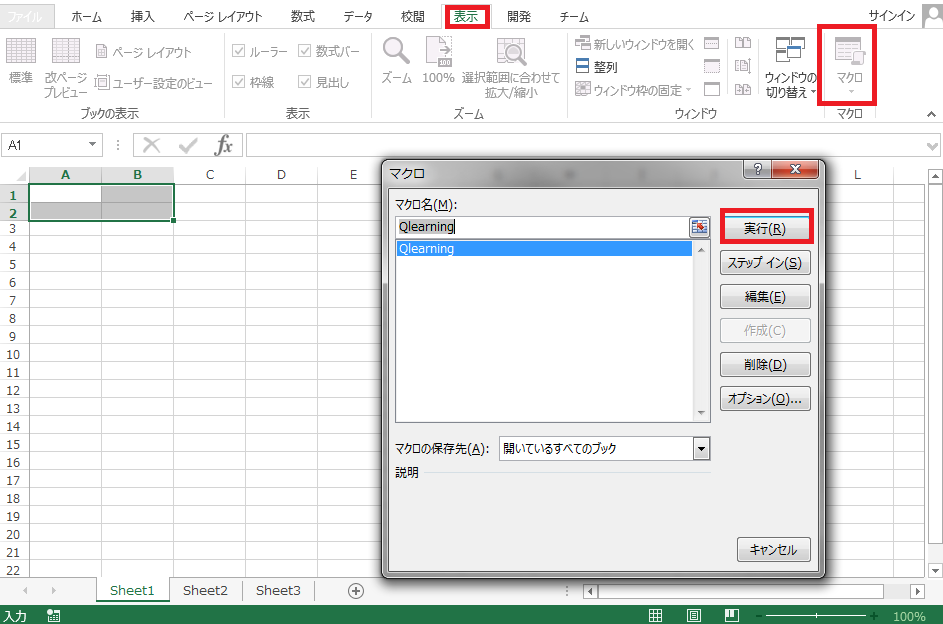
セルA1, A2, B1, B2に$Q$値の初期値0がセットされます。セルはそれぞれ
-
A1は(状態1(電球点灯), 行動1(ボタン1を押す))の $Q(1,1)$ -
A2は(状態2(電球消灯), 行動1(ボタン1を押す))の $Q(2,1)$ -
B1は(状態1(電球点灯), 行動2(ボタン2を押す))の $Q(1,2)$ -
B2は(状態2(電球消灯), 行動2(ボタン2を押す))の $Q(2,2)$
を表しています
行動選択手法を選ぶフォームが立ち上がるので、ε-greedyなら1をSoftmaxなら2を入力してOKを押します。
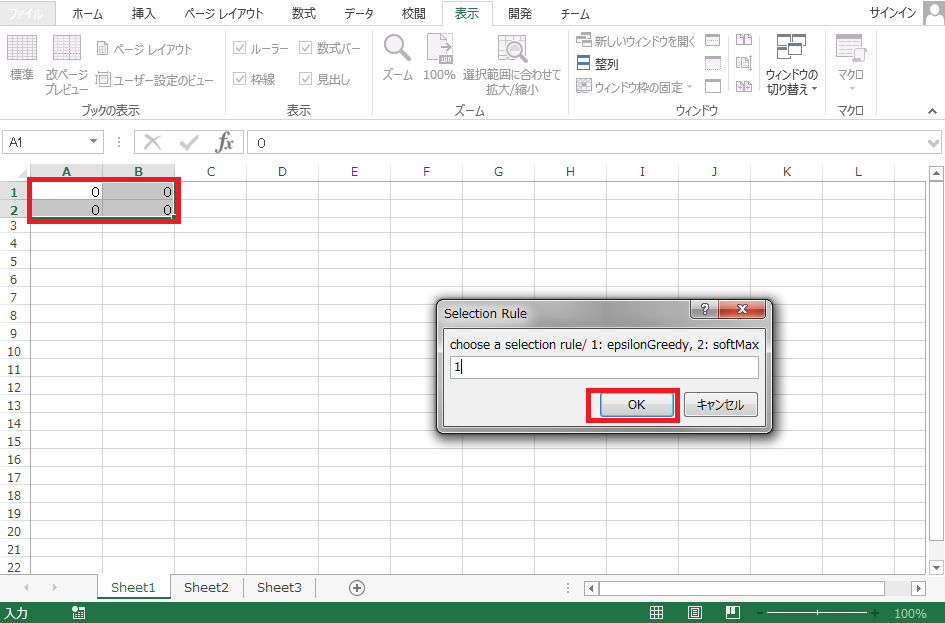
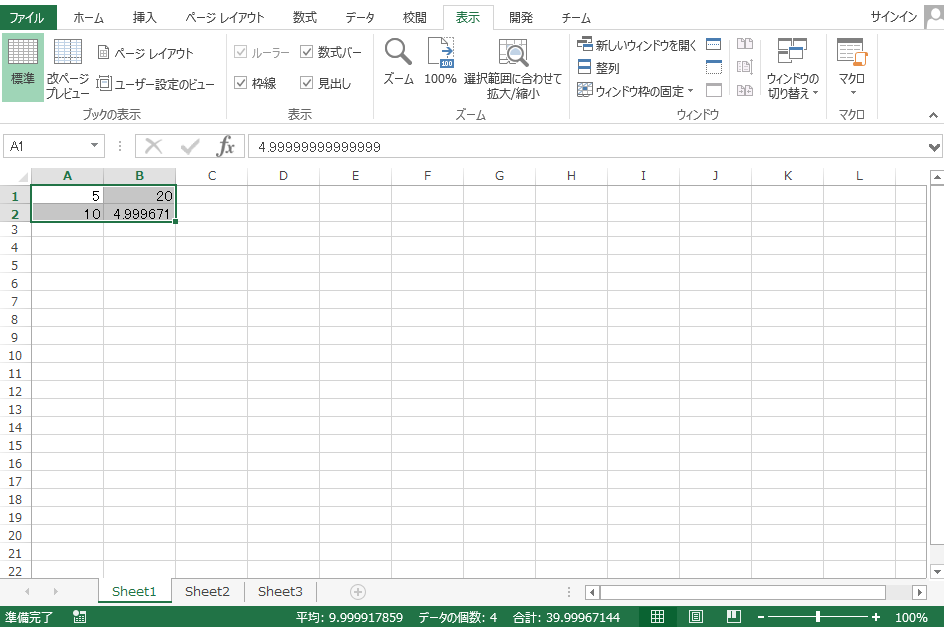
計算が完了すると下記の図のように出力されます。出力結果からセルB1とセルA2の$Q$値が大きくなるように学習が進んだことがわかります。これは学習して欲しかった行動を選択するように学習したことを示しています。つまり学習が進行することで、電球が点灯している時にはボタン2を押してチーズを製造し、電球が消灯しているときはボタン1を押して電球を点灯させるように行動選択するようになっています。
$Q$値の初期値が0から学習が進行しているので、学習の初期の段階では確率的に可能な行動を広く探索しています。このためセルA1やセルB2にもセルA2やセルB1よりも小さい値が出力されています。
まとめ
今回は強化学習の一つであるQ-learningを, 行動選択手法としてε-greedy, Softmax について簡単なExcelのVBA実装例を紹介してきました。VBAを活用するとちょっとした機械学習の実験はできてしまうので便利です。本格的な実装の前の下書きとして、さくっとモデルの色々な振る舞いを調査したい時(特に非エンジニアとコミニュケーションしながらモデルを素早く作る必要がある時)なんかに重宝します。
===========================================
こちらもよろしくおねがいいたします。
入門編
第1部イントロダクション
第2部エクセルで学ぶ分析入門
- 第3章:ExcelとMySQLの連携
- 第4章:ExcelとMySQLの連携2 csvデータのimport
- 第5章:Excelの分析ツールとソルバーの活用(回帰、最小2乗法)
- 第6章:Excelソルバーの応用(ポートフォリオ最適化)
第3部 データ可視化(ビッグデータに限らない)
==================