まえがき
今回も始まりました。やってみよう分析!シリーズ
前章まではExcelとMySQLを連携させ、csvをMySQLに読み込んだりpivotを利用する方法を紹介しました。本章ではMySQLから離れ、Excelのアドインツールである分析ツールとソルバーを紹介します。本章で紹介する項目は下記のとおりです。
- 分析ツールとソルバーの導入
- 分析ツールで回帰
- ソルバーで回帰
- ソルバーの応用:最小2乗法により曲線のフィッティング
※本章はExcel2010以降で動作します。
分析ツール、ソルバーとは
Excelを活用することでpivotを駆使し、ドリルダウン形式の分析はかなりのことが行えます。さらにMySQLと連携させることで中規模程度のデータの分析なら比較的簡単に分析することが可能です。一方、単純なクロス集計以上の分析が必要になる場合もあります。例えば回帰分析、関数のフィッティングやフーリエ変換、相関、t検定などです。
Excelではこれらの分析に対応する便利機能がアドインツールとして備わっています。それが分析ツールとソルバーです。
分析ツールは回帰分析をはじめフーリエ変換、相関、t検定、ヒストグラムなどを扱うことが可能です。ソルバーは与えられた関数を制約条件のもとで最大・最小にする解を探すツールです。ソルバーを用いることで最小2乗法を実行することが可能になります。
本章では回帰分析や最小2乗法を通じて分析ツールやソルバーを紹介したいと思います。
それでは早速始めましょう。
※本章の数式はIEではうまく表示されない可能性があります。その場合にはfirefoxかchromeをご利用ください。
分析ツールとソルバーの導入
Excelのアドインである分析ツールとソルバーを使うための準備を行いましょう。分析ツールとソルバーは デフォルトで使える状態になっていません。使うためにはExcelに対して若干の事前設定が必要です。
Excelを起動してファイルタブを開きます。
続いてオプションを選択、Excelのオプションウィンドウが立ち上がるので、そこで __アドイン__を選びます。
管理の項目の設定ボタンを押します。
アドインウィンドウが立ち上がったらソルバーアドインと分析ツールにチェックを入れます。
これでデータタブの右側にソルバーとデータ分析という項目が出現するはずです。これで分析ツールとソルバーを使う準備が整いました。
分析ツールで回帰
分析ツールを実際に使ってみましょう。データタブのデータ分析を選択します。起動したデータ分析ウィンドウを眺めると様々な分析機能が利用できることがわかります。ここでは具体例として __回帰__を使ってみます。
注意点:
分析ツールの回帰分析は16変数までしか対応していないようです。
16変数以上の回帰を実行したい場合は後に紹介するソルバーを活用します。
回帰分析に使うデータは次の表で与えられているサンプルです。yは目的変数、x1, x2は説明変数です。サンプルデータをラベルからコピーしてExcelのA1セルから貼り付けておきます。
| y | x1 | x2 |
|---|---|---|
| 2.69826805341837 | 1.8 | -2 |
| 6.96569058344701 | 2.6 | -1 |
| 6.18147132412193 | 3.4 | 0 |
| 8.37978437764752 | 4.2 | 1 |
| 6.0051043745755 | 5 | 2 |
| 12.7503658226301 | 5.8 | 3 |
| 12.1576077418813 | 6.6 | 4 |
| 12.5347233929621 | 7.4 | 5 |
| 11.0457038187897 | 8.2 | 5 |
| 13.4184213352584 | 9 | 3 |
| 14.6054042013499 | 9.8 | -6 |
| 12.9727602710346 | 10.6 | -2 |
| 14.3599299573675 | 11.4 | -4 |
| 17.3156976325483 | 12.2 | -2 |
| 18.8655316686173 | 13 | -1 |
| 19.7886318147084 | 13.8 | 0 |
| 18.9788564679526 | 14.6 | 1 |
| 23.7040154134375 | 15.4 | 2 |
| 22.548120870201 | 16.2 | 3 |
| 25.656091697348 | 17 | 4 |
| 24.1410686641567 | 17.8 | 5 |
| 24.2236426127884 | 18.6 | 6 |
| 24.2800396830984 | 19.4 | 7 |
| 29.7739345968256 | 20.2 | 8 |
| 28.2426177814177 | 21 | 4 |
| 26.9600411211083 | 21.8 | 7 |
| 30.0154078000902 | 22.6 | 5 |
| 32.0455071562674 | 23.4 | 6 |
| 30.6867241964618 | 24.2 | 7 |
| 35.8751707541474 | 25 | 8 |
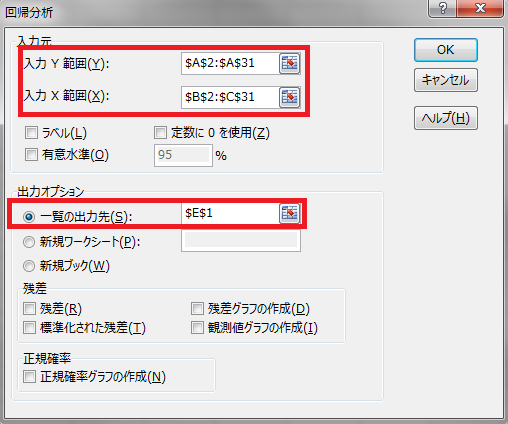
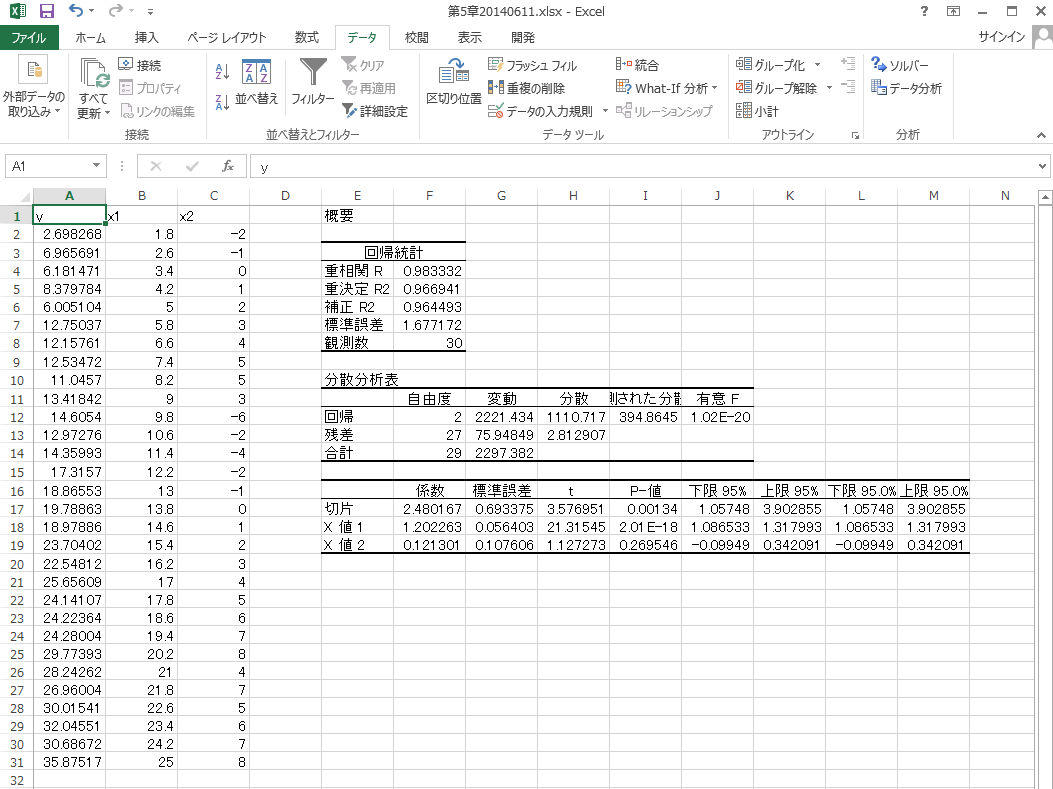
Excelのシート上にはデータがA列にy(A1はラベル), B列にx1(B1はラベル), C列(C1はラベル)にx2が挿入されているとします。その上で回帰分析のウィンドウの入力範囲と出力オプションに次の図のようにセル領域を指定します。
そしてOKボタンを押すと結果が出力されます。結果には推定したパラメータに加えて決定係数やp値等の統計量も同時に表示されるので便利です。
ソルバーで回帰
ソルバーとは
ソルバーはある目的の値を最大または最小化させるためのパラメータ(解)を探すときに使います。解の探索条件として制約条件が付いているケースにも活用できます。
Excelソルバーの解探索の方法にはGRG(Generalized Reduced Gradient)非線形、シンプレックスLP、エボリューショナリーの3つあります。GRG非線形はなめらかな非線形関数の最大最小を探すのに用います。シンプレックスLPは線形問題を解くときに使います。エボリューショナリーは滑らかではない非線形関数に対して問題を解くときに使われます。
回帰直線を求める
ここでは回帰直線を得るために、回帰パラメータを最小2乗法で求める方針で進めます。そのために分析ツールで使ったデータに対して
\sum_{i}(y_{i}-a_{1}x_{1i}-a_{2}x_{2i}-b)^{2}
を最小化させるパラメータa1, a2, bをソルバー(GRG非線形)を使って探すことにします。ソルバーを使って見つけられたパラメータは分析ツールのそれらと同じになるはずです。
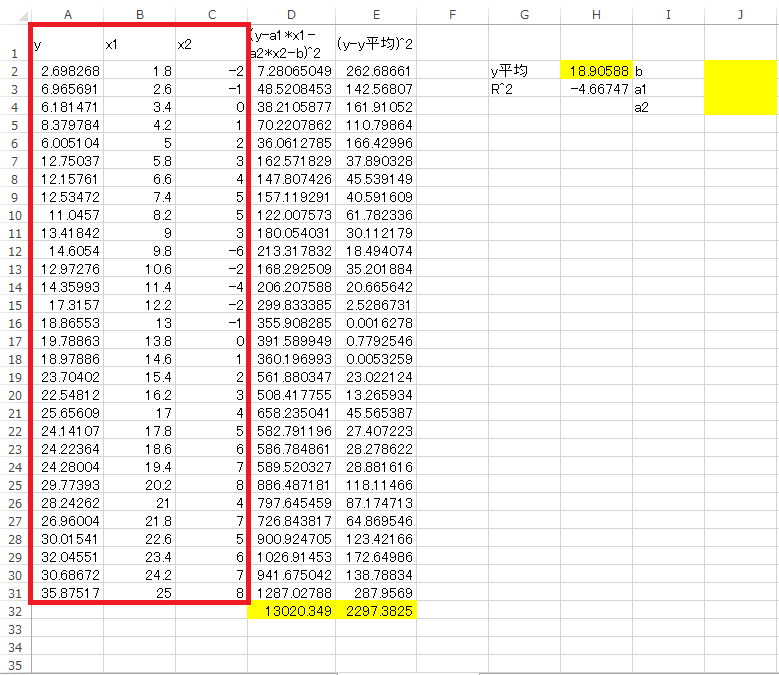
Excelシートの準備
分析ツールの紹介で使ったデータを再度、シートにA1から貼り付けます。
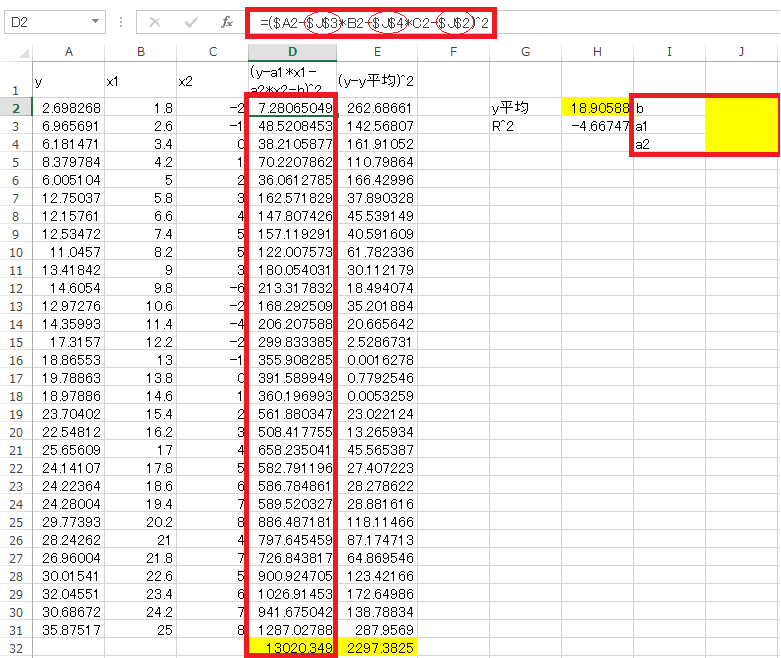
次にセルD2に=($A2-$J$3*B2-$J$4*C2-$J$2)^2と式を入力し31行目までコピーペーストします。ここでJ2, J3, J4はこれから求めるパラメータです。続いてセルD32にD2からD31まで和を入力します(=SUM(D2:D31))。この値が最小2乗法で最小化させる式になります。あとでこの式をソルバーを使って最小化させます。
さらに直線回帰の当てはまりの目安である決定係数R^2を求めます。決定係数R^2としては次の定義を使います。
R^{2} \equiv 1 - \frac{\sum_{i} (y_{i} - a_{1}x_{1i}-a_{2}x_{2i}-b)^{2}}{\sum_{i} (y_{i} - \bar{y})^{2}}
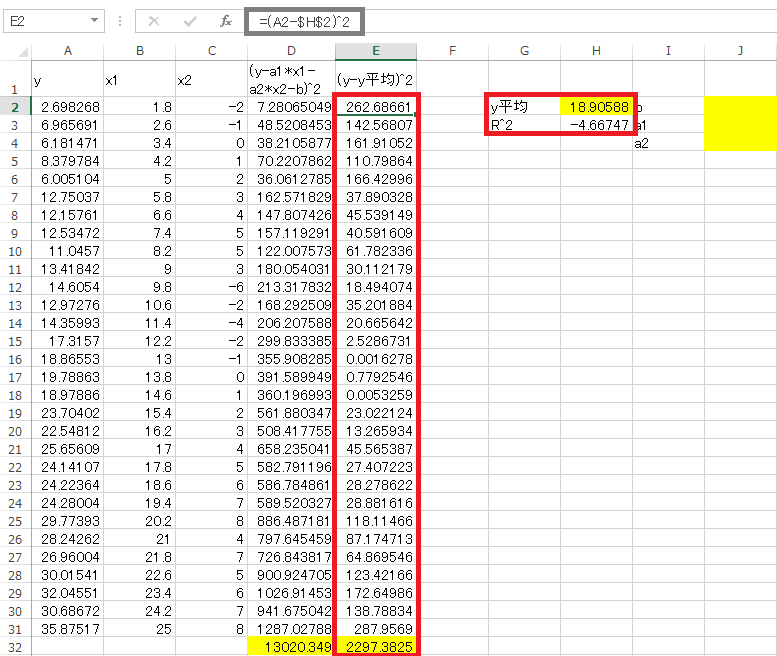
セルH2にyの平均値=AVERAGE(A2:A31)を代入します。次にセルE2に=(A2-$H$2)^2と入力してセルE31までコピーペーストします。次にE列の値を足します=SUM(E2:E31)。最後にセルH3に=1-(D32/E32)を入力します。
これでソルバーを使う準備が完了です。
ソルバー適用
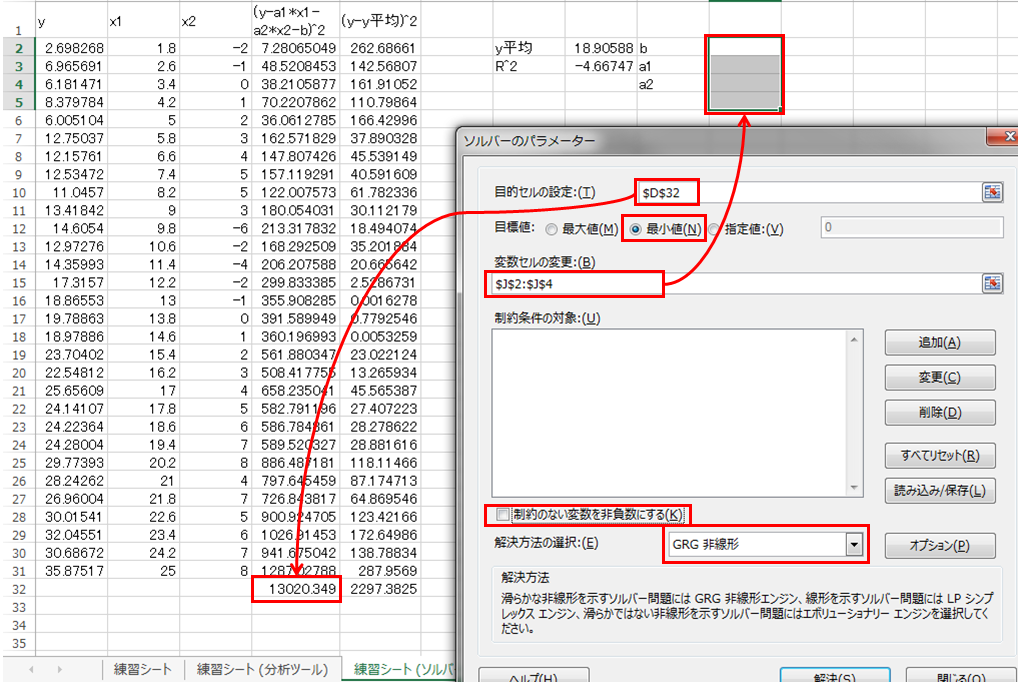
ソルバーを起動させます。Excelのデータタブからソルバーを立ち上げます。ソルバーのウィンドウだ立ち上がったら次のように設定します。
- 目的セルの設定:
$D$32 - 目標値:最小値
- 変数セルの変更:
$J$2:$J$4 - 制約のない変数を非負数にするのチェックを外す
- 解決方法の選択:GRG 非線形
更にソルバーのオプションボタンを押します。GRG非線形タブを開き、微分係数を中央、マルチスタートを使用するを選択します。
ここで微分係数が前方と中央の違いは目的関数f(x)を探索するときに使われる
x_{(t+1)} \simeq x_{(t)} + h \nabla f(x_{(t)}) + \cdots
の偏微分∇の定義の相違です(ここでhは差分のサイズ)。おそらくソルバーウィンドウの前方は前方差分、中央は中央差分を意味していると思われます。例えば、目的関数が1変数xのみに依存する場合、その前方差分と中央差分はそれぞれ
f'(x) = \frac{f(x + h) - f(x)}{h} \\
f'(x) = \frac{f(x + h) - f(x-h)}{2h}
で与えられます。前方差分と中央差分では誤差に相違が現れます(中央差分のほうが誤差が小さい)。今は中央差分を選択します。
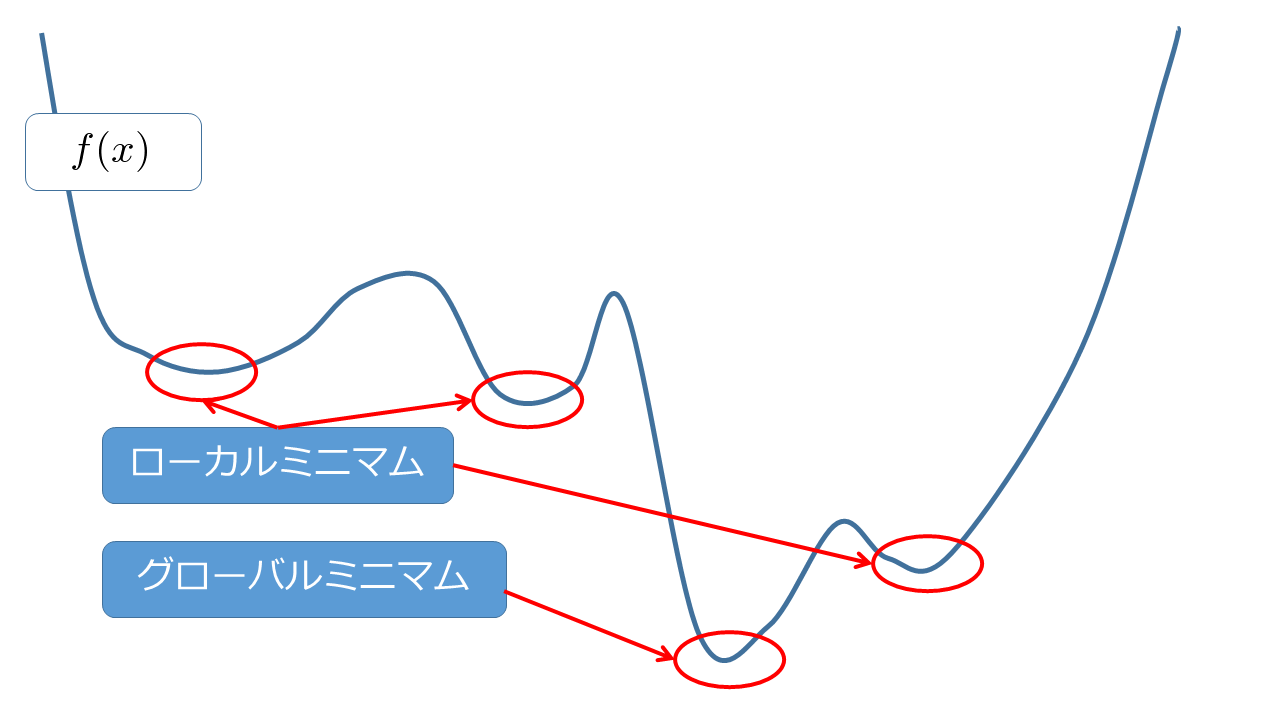
マルチスタートは目的関数の探索を複数の初期点から開始する機能です。一般に目的関数の極値は複数存在します(微分係数が0になる点 = 曲線(曲面)が部分的にフラットになる場所)。そのなかで局所的な最小点(ローカルミニマム)だけではなく、大域的な最小点(グローバルミニマム)を探すためマルチスタートが利用されます。
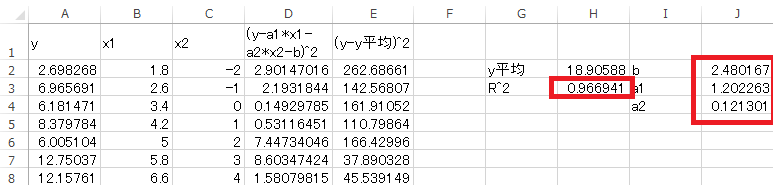
これらの設定でOKボタンを押し、解決ボタンを押します。ソルバーが成功すると決定係数R^2と回帰パラメータa1, a2, bが出力されます。これらの値は分析ツールで求めた重決定R^2, 切片(b), X 値1(a1), X 値2(a2)と(ほぼ)同じになります。
ソルバーの応用:最小2乗法により曲線のフィッティング
線形回帰で紹介したソルバーによる最小2乗法を活用することで、直線だけではなく曲線のフィッティングも可能です。具体的に次のテストデータを記述する関数を最小2乗法でフィッティングしてみます。ここでもyが目的変数、x1が説明変数です。
| y | x1 |
|---|---|
| 0 | 1.8 |
| 0.142083083253392 | 2.6 |
| 0.300563312084574 | 3.4 |
| 0.460554099095599 | 4.2 |
| 0.612299649437676 | 5 |
| 0.750132371006099 | 5.8 |
| 0.871450737653146 | 6.6 |
| 0.975752440276106 | 7.4 |
| 1.0638364450157 | 8.2 |
| 1.1372099161805 | 9 |
| 1.19768292444043 | 9.8 |
| 1.24711236361406 | 10.6 |
| 1.28725401763837 | 11.4 |
| 1.31968773070409 | 12.2 |
| 1.34578899868191 | 13 |
| 1.36672812641056 | 13.8 |
| 1.38348436168448 | 14.6 |
| 1.39686701248518 | 15.4 |
| 1.40753873047023 | 16.2 |
| 1.41603824058394 | 17 |
| 1.42280112554724 | 17.8 |
| 1.42817808177546 | 18.6 |
| 1.43245053041605 | 19.4 |
| 1.43584371895325 | 20.2 |
| 1.43853756892314 | 21 |
| 1.44067556801164 | 21.8 |
| 1.44237200442472 | 22.6 |
| 1.44371781894037 | 23.4 |
| 1.444785317972 | 24.2 |
| 1.44563195641537 | 25 |
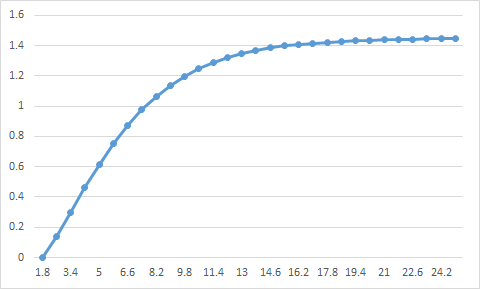
このデータをプロットすると次のような曲線であることがわかります(縦軸y、横軸x1)。
この曲線を次の関数系を仮定してパラメターa1, a2, a3, bを最小2乗法で推定してみます。
\sum_{i}( y_{i} - a_{1}x_{1i} - a_{2} x_{2i}^{2} - a_{3} x_{3i}^{3} - b )^{2}
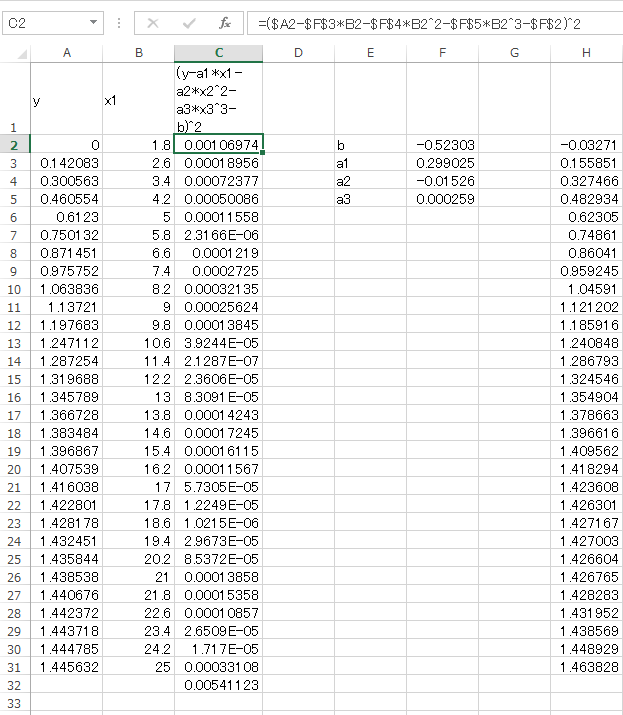
推定する手順は回帰の方法と同じです。上記のデータをExcelシートのセルA1から貼り付けます。セルC2に=($A2-$F$3*B2-$F$4*B2^2-$F$5*B2^3-$F$2)^2と入力し、C31までコピーペーストします。C32にはC2からC31までの和を入力します(=SUM(C2:C31))。
出力される推定パラメータを使った曲線の確認のため、セルH2に=$F$2+$F$3*B2+$F$4*B2^2+$F$5*B2^3を入力しH31までコピーペーストします。
続いてソルバーを起動します。目的セルの設定に$C$32、変数セルの条件に$F$2:$F$5、制約のない変数を非負数にするのチェックを外し、解決の方法の選択でGRG 非線形を選択します。オプションボタンを押し、GRG 非線形タブを開いて微分係数を中央を選択、マルチスタートを使用するにチェックを入れます。そしてOKボタン→解決ボタンでソルバーを実行します。
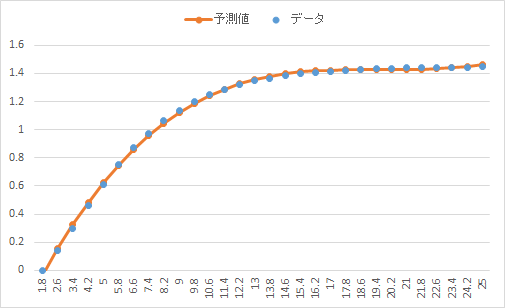
Yのデータ(A列)とフィッティング式から出力されたデータ(H列)をプロットすると次のグラフのようになります。このようにソルバーを使うと曲線をデータから比較的容易に推定できます。
まとめ
本章ではExcelのアドインである分析ツールとソルバーを紹介してきました。ツール利用の具体例として回帰分析や最小2乗法をサンプルデータに対して実行してみました。分析ツールは解析できる変数が16個に限定されていましたが、p値などの統計量も自動で出力してくれるので便利でした。ソルバーは直線回帰以外にも曲線にフィッティングにも応用可能でした。
本章では紹介してきませんでしたが、分析ツールには回帰以外にもフーリエ変換や分散を求めたりと様々な機能が搭載されています。興味を持たれた方はいろいろ試してみることをおすすめします。
ソルバーは解探索したい関数と制約条件さえ与えれば、自動で解を探してくれるので応用の自由度が非常に高いです。次章ではソルバー活用の分析応用例をさらに紹介したいと思います。
===========================================