まえがき
今回も始まりました。やってみよう分析!シリーズ
前章ではExcelの分析ツールとソルバーを活用して回分析や帰や曲線のフィティングの方法を紹介しました。本章では前章に引き続きソルバーに焦点を当て、ソルバーを使ったポートフォリオ最適化問題の解き方について、基本的事項を紹介します。
本章で扱うポートフォリオ最適化問題は金融の例を扱います。想定しているのは、ある投資家が手持ちの資金をいくつかの証券に分散投資する場面を考えます。この時、どのように資金を配分すると最も利益を得ることができるかを考える。これがポートフォリオ最適化問題のあらましです(本章では金融工学を専門的に扱うことは意図していなので、このくらいのイメージで十分です)。
本章で紹介する項目は下記のとおりです。
- ポートフォリオ最適化問題
- 平均-分散モデル
- コンパクト分解表現
- 平均-絶対偏差モデル
- Excelソルバーでポートフォリオ最適化問題を解く
では早速始めましょう!
ポートフォリオ最適化問題を解くときの方針
※本節は難しければこの先の"Excelソルバーで平均-絶対偏差モデルを解く"に進んでください。
まずはじめに問題の詳細に入る前に、ポートフォリオ最適化問題を解くための方針を説明します。次のような具体的問題設定を考えます。
問題
投資家が4つの何らかの証券l_1からl_4に分散投資することを考えます。これら証券の __収益率__がR_i(i=,1,2,3,4)で与えられると、全収益率は __投資配分比率__をw_i( w_1+w_2+w_3+w_4=1)として次の様に与えられます。
r=\sum_{i=1}^{4} E[R_{i}]w_{i}, \qquad \sum_{i=1}^{4}w_{i} = 1, \qquad w_{i} \geq 0
ここでE[*]は期待値を表しています。この全収益率rを、 リスク尺度(risk measure) RMと呼ばれる量を最小化させつつ、ある目標全収益率r_targetより大きくさせる投資配分比率を求める問題を考えます。リスク尺度は投資配分比率の関数です(RM=RM(w))。まとめるとここでのポートフォリオ最適化問題は次のように定式化されます。
\text{Minimize}~~ \text{RM}(w)\\
\text{subject to} \\
r=\sum_{i=1}^{4} E[R_{i}]w_{i} \geq r_{\text{target}}, \qquad \sum_{i=1}^{4}w_{i} = 1, \qquad
w_{i} \geq 0 ~~(i=1,2,3,4)
制約条件の数は必要に応じて更に増えることがあります。
リスク尺度とは
リスク尺度とは、大雑把には全収益率の期待値がどれくらい上下にブレるか示した量です。リスク尺度が大きくなるように投資配分すると、得られるリターンが期待より大きくなる見込みがある一方で、大きく下ブレることも予想されます。逆にリスク尺度が値が小さくなるような投資配分比率であれば、期待収益率が大きく上振れることは少ないですが大きく下振れることを防ぐことができます。
ポートフォリオ最適化ではリスク尺度を最小化させることをよく考えます。これは暗に 投資家がリスク回避を選好していると考えるためです。リスク尺度の選択によって投資配分比率や期待収益率のパフォーマンスが異なってきます。
本章では最適化問題をどうやってExcelソルバーで解くのかに焦点を当てています。ポートフォリオの様々なモデルや特徴については下記の文献をご参照ください。
- 金融工学と最適化 (経営科学のニューフロンティア 5) 枇々木 規雄, 朝倉書店
- 投資信託を用いた個人投資家の資産運用モデル 山本零, 『ファイナンシャル・プランニング研究』NO.8
平均-分散モデル
平均-分散モデルはポートフォリオ選択問題に対する代表的なモデルです。このモデルで期待収益率の分散をリスク尺度とし、それを最小にするように投資配分比率を選択するモデルになっています。
平均-分散モデルでは各証券の収益率の期待値と分散は次のように過去の収益率時系列データR_itから求めることができるとします。
r_{j} \equiv E[R_{j}] = \frac{1}{T}\sum_{t=1}^{T} R_{jt} \\
r = \sum_{i=1}^{4} r_{i}w_{i} \\
V(R) = E[(R-E[R])^{2}] =
\sum_{i=1}^{4} \sum_{j=1}^{4} \Biggl\{ \frac{1}{T} \sum_{t=1}^{T}(R_{it}-r_{i})(R_{jt}-r_{j}) \Biggr\}
w_{i} w_{j}
= \sum_{i=1}^{4} \sum_{j=1}^{4} \sigma_{ij} w_{i} w_{j}
したがって平均-分散モデルのポートフォリオ最適化問題は次のように定式化されます(下記の条件を満たしつつ分散を最小化させるような投資配分比率w_iを見つける問題)。
\text{Minimize}~~ \sum_{i=1}^{4} \sum_{j=1}^{4} \sigma_{ij} w_{i} w_{j} \\
\text{subject to} \\
r \geq r_{\text{target}}, \qquad \sum_{i=1}^{4}w_{i} = 1, \qquad
w_{i} \geq 0 ~~(i=1,2,3,4)
コンパクト分解表現
上記の数理計画問題は __コンパクト分解表現__と呼ばれる形式にも書き換えることが可能です。問題をコンパクト分解表現にすることで問題の見通しが良くなったり、解きやすくなったりするメリットがあります。
平均-分散モデルをコンパクト分解表現に書き換えるために、分散が次のように書き換えることが可能であることに注目します。
V(R) = \frac{1}{T} \sum_{t=1}^{T}
\Biggl\{ (\sum_{i=1}^{4} R_{it} w_{i}-r)(\sum_{j=1}^{4} R_{jt}w_{j}-r) \Biggr\}
\equiv \frac{1}{T} \sum_{t=1}^{T} y_{t}^{2}, \\
y_{t} \equiv \sum_{i=1}^{4} R_{it} w_{i}-r
y_tは新たに導入された変数です。この事実を使うと平均-分散モデルのポートフォリオ最適化問題は次のように書き換えられます。
\text{Minimize}~~ \frac{1}{T} \sum_{t=1}^{T} y_{t}^{2} \\
\text{subject to} \\
\sum_{i=1}^{4} R_{it} w_{i} - y_{t} = r, \\
r \geq r_{\text{target}}, \qquad \sum_{i=1}^{4}w_{i} = 1, \qquad
w_{i} \geq 0 ~~(i=1,2,3,4)
平均-絶対偏差モデル
平均-絶対偏差モデルでは分散の代わりに次の 絶対偏差(absolute deviance)をリスク尺度として採用します。
AD(R) = \frac{1}{T} \sum_{t=1}^{T} \Biggl| \sum_{i=1}^{4}R_{it}w_{i}-r \Biggr|
この量には絶対値が含まれています。コンパクト分解表現を使うと平均-絶対偏差モデルを線形計画問題として扱うことができます。これを実現させるために次のような関係を定義します。
y^{+}_{t} \geq 0, \qquad y^{-}_{t} \geq 0, \\
y^{+}_{t} + y^{-}_{t} = \Biggl| \sum_{i=1}^{4}R_{it}w_{i}-r \Biggr|, \\
y^{+}_{t} - y^{-}_{t} = \sum_{i=1}^{4}R_{it}w_{i}-r \Rightarrow
\sum_{t=1}^{T} y^{+}_{t} =
\begin{cases}
\sum_{t=1}^{T} y_{t} \geq 0 \\
y^{+}_{t} = \sum_{i=1}^{4}R_{it}w_{i}-r +y_{t} \geq 0
\end{cases}
このとき平均-絶対偏差モデルでポートフォリオ最適化問題は次のように線形計画問題として書き表すことができます。
\text{Minimize}~~ \frac{1}{T} \sum_{t=1}^{T} y_{t} ~~~(y^{-}_{t} \equiv y_{t})\\
\text{subject to} \\
\sum_{i=1}^{4} R_{it} w_{i} + y_{t} \geq r ~~(t=1, \cdots , T), \\
y_{t} \geq 0, ~~r \geq r_{\text{target}} ~~(t=1, \cdots , T), \\
\sum_{i=1}^{4}w_{i} = 1, ~~w_{i} \geq 0 ~~(i=1,2,3,4)
書き換えるための条件
絶対偏差ADの絶対値の部分をy_tで書き表せるためには次の条件が必要です。まず上記の絶対偏差が最小になる解が次の条件を満たしているとします。
y^{+}_{t} > 0, ~y_{t} = y^{-}_{t} >0 \rightarrow ( z^{+}_{t},z^{-}_{t} ) =
\begin{cases}
(y^{+}_{t} - y^{-}_{t}, ~0) \text{ if } y^{+}_{t} \geq y^{-}_{t}\\
(0, ~y^{-}_{t} - y^{+}_{t} ) \text{ if } y^{+}_{t} < y^{-}_{t}
\end{cases}
このとき
z^{+}_{t} + z^{-}_{t} < y^{+}_{t} + y^{-}_{t}
となります。これは最小解であると仮定したにもかかわらず、それよりも小さい値が存在することを意味しています。したがって __y^{+}_{t}とy^{-}_{t}はどちらか一方が0であること__が必要です。逆に最小解が見つかった時にはどちらか一方は0であるという事になります。
Excelソルバーで平均-絶対偏差モデルを解く
今までは平均-分散モデルや平均-絶対偏差モデルの理論的背景を説明してきました。ここでは具体的に平均-絶対偏差モデルをExcelソルバーを使って説いてみたいと思います。平均-絶対偏差モデルは上述してきたように線形計画問題として定式化できるので、Excelソルバーで簡単に解くことができます(扱える変数の数に制約はありますが)。線形計画問題用のソルバーライブラリなら様々なプログラミング言語向けで比較的フリーのものを見つけやすいので、そういう意味でも平均-絶対偏差モデルは実用的にも扱いやすいと思われます。
ここで扱うテストデータは下記のものです。これはある4つの仮想収益率を時系列で29日分を表しているとしています。
| 日付 | l_1 | l_2 | l_3 | l_4 |
|---|---|---|---|---|
| 1 | -0.00120153065421321 | 0.0380048089808824 | -0.000303873486371429 | 0.0183133857272363 |
| 2 | -0.00875319764093676 | 0.00750730657101174 | 0.0187881175156959 | 0.00405168168299995 |
| 3 | 0.0141313057519581 | -0.00480224587721186 | 0.0211116532539269 | -0.00859677575024866 |
| 4 | -0.00026089277347954 | -0.00432006835634278 | -0.00671115000654706 | 0.0205754516520216 |
| 5 | 0.0230835221631592 | 0.0428244722829147 | 9.90283983480213E-05 | -0.00247133285460752 |
| 6 | 0.0278628771011717 | -0.019356828954738 | -0.00740798431316384 | -0.00101736234100942 |
| 7 | 0.0130697045380814 | 0.0188506465519101 | -0.00523275574503766 | 0.0445910602540186 |
| 8 | 0.0411167849440832 | -0.0210227558705826 | 0.0105982386670339 | 0.0181642469063737 |
| 9 | 0.00862197349532295 | 0.0194908416797854 | 0.0245934046268627 | 0.00709581280876198 |
| 10 | 0.0166329870758843 | 0.00983444518545119 | 0.030223257019714 | 0.0158169011616007 |
| 11 | 0.0251692450492102 | 0.0234264530594299 | 0.0485315350214701 | 0.0169290052447109 |
| 12 | 0.0036280008797798 | -0.0238983867296893 | 0.0221588090462638 | -0.0212142656439686 |
| 13 | 0.0364523781300635 | 0.0453273177976274 | 0.00684582294461588 | 0.0169143763754707 |
| 14 | 0.0212167263941988 | 0.0351431617328777 | -0.0217647873161181 | 0.0383881403307489 |
| 15 | -0.0165150470435798 | 0.0319588787470421 | 0.0440612973224269 | 0.0371634615256434 |
| 16 | -0.0209412151441614 | -0.00594844301585869 | 0.0390005824355782 | 0.0234988931994846 |
| 17 | -0.0163049250497025 | 0.0235517455011055 | 0.0254367405717981 | 0.0478825651627125 |
| 18 | 0.0218889495295429 | -0.00390039496419029 | 0.00999515377794965 | 0.0025776781494086 |
| 19 | 0.000167684857827004 | 0.000127471697942828 | 0.0187525342938277 | 0.0379500995171109 |
| 20 | 0.0320038917185764 | -0.0158606942769403 | 0.0348337189422131 | -0.00187666832618083 |
| 21 | 0.0181514768796902 | -0.0176344811110534 | -0.0189057906647764 | -0.0208109253641162 |
| 22 | 0.0241881816658587 | 0.0455000763886743 | 0.011393810955836 | 0.0199381468086756 |
| 23 | -0.017270902625127 | -0.01820057224978 | 0.0246536997732942 | 0.0134747443795706 |
| 24 | 0.0336124764557386 | 0.0369219499655584 | 0.033199777646845 | 0.0238727536930151 |
| 25 | -0.000756539563920317 | 0.00565398148175538 | 0.0221568251473784 | 0.00256183858438883 |
| 26 | 0.0458304879491117 | 0.00439694780137093 | 0.025492911991075 | 0.00558063721177299 |
| 27 | 0.0266866459295242 | 0.013707194604382 | 0.0285421934279625 | 0.0272808773191875 |
| 28 | 0.0371346323314259 | 0.0509490436623156 | -0.0220063375794736 | -0.00732380784203699 |
| 29 | 0.0501540409823486 | 0.0297740391226334 | 0.0169058439224333 | 0.00451478718620258 |
改めて平均-絶対偏差モデルの問題を思い出しておきます。R_jtがj番目のt日目収益率を表しているとして下記の問題を解くことで投資配分比率w_iを求めます(T=29)。
\text{Minimize}~~ \frac{1}{T} \sum_{t=1}^{T} y_{t} \\
\text{subject to} \\
r_{j} = \frac{1}{T}\sum_{t=1}^{T} R_{jt}, \qquad r = \sum_{i=1}^{4} r_{i}w_{i} \\
\sum_{i=1}^{4} R_{it} w_{i} + y_{t} \geq r ~~(t=1, \cdots , T), \\
y_{t} \geq 0, ~~r \geq r_{\text{target}} ~~(t=1, \cdots , T), \\
\sum_{i=1}^{4}w_{i} = 1, ~~w_{i} \geq 0 ~~(i=1,2,3,4)
Excelシートの準備
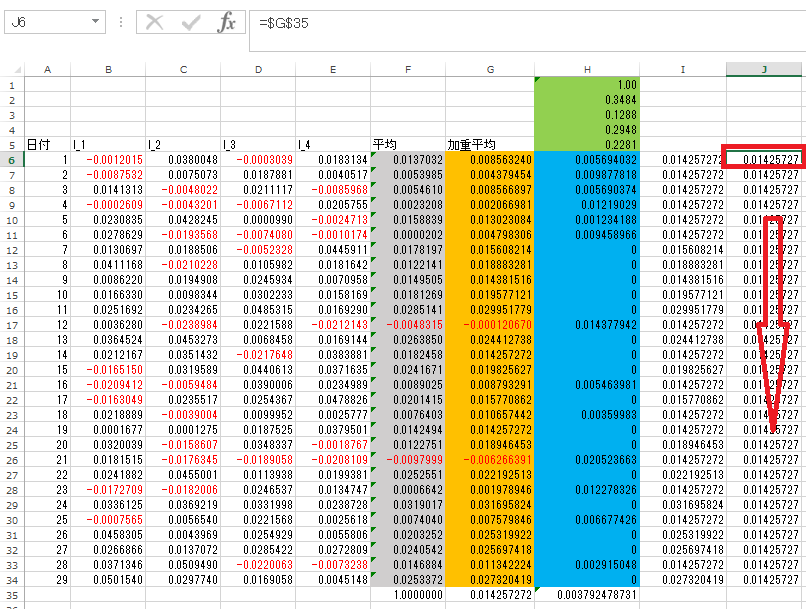
上記テーブルのデータをラベルも含めてまるっとエクセルのシートにA5セルから貼り付けます。
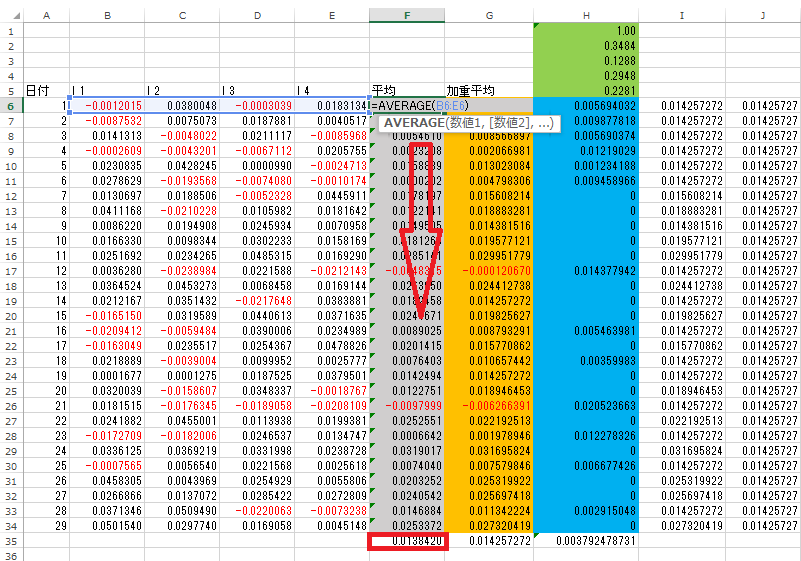
セルF6にl_1からl_4までの平均を算出します。その式を29日めまでコピーペーストします。最後にセルF35にF6からF34までの平均値を入力します(=AVERAGE(F6:F34))。
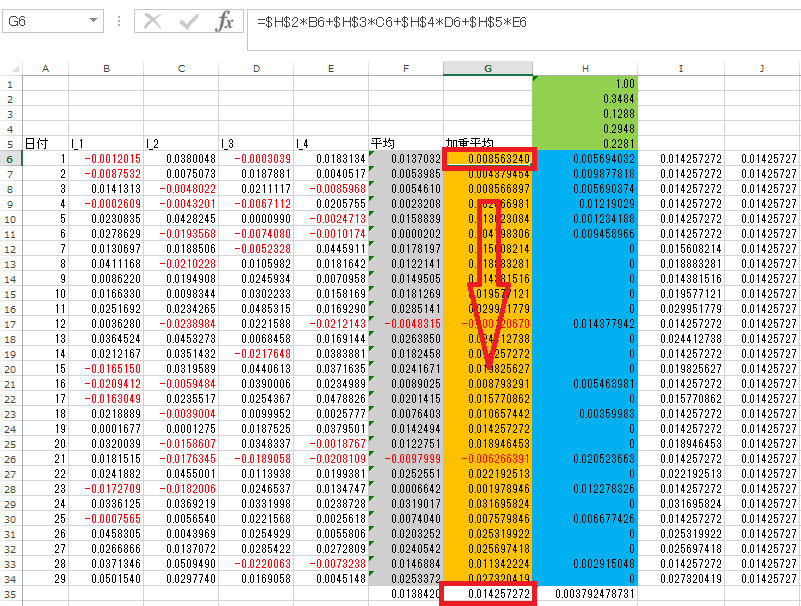
次はG6セルに=$H$2*B6+$H$3*C6+$H$4*D6+$H$5*E6と入力します(投資配分比率がセルH2からH5までw_1からw_4の順で並んでいるとしています)。入力した式を29日めまでコピーペーストします。続いてセルG35にセルG6からG34までの平均値を入力します(=AVERAGE(G6:G34))。
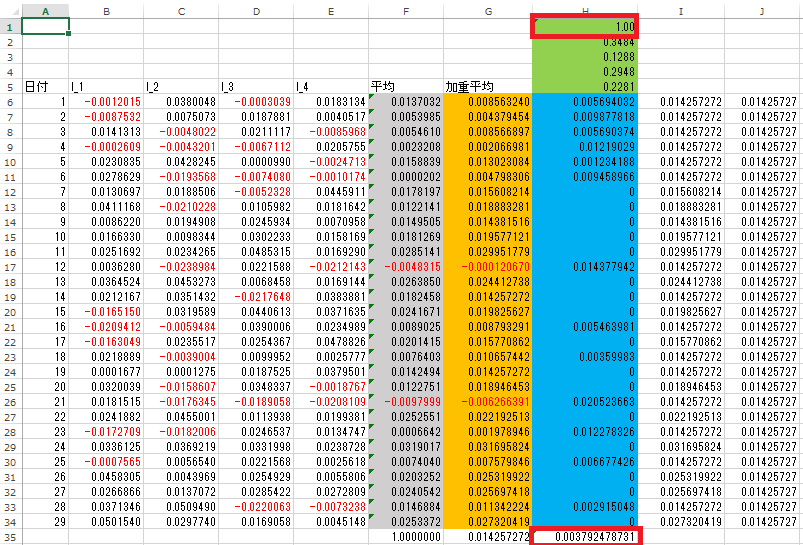
セルH1に=SUM(H2:H5)と入力します。またセルH35に=AVERAGE(H6:H34)と入力します。
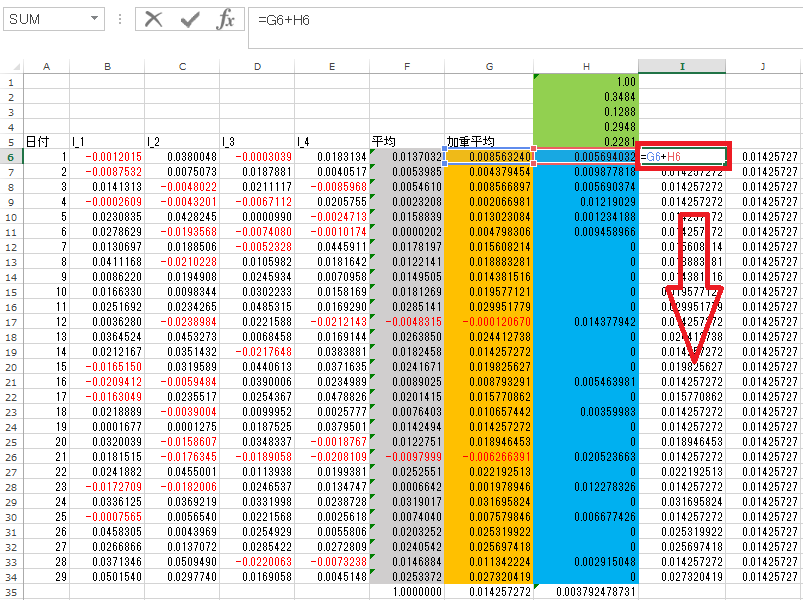
セルI6に=G6+H6と入力します。この式をセルF34までコピーペーストします。
セルJ6に=$G$35と入力してセルF34までコピーペーストします。
ソルバーで解く
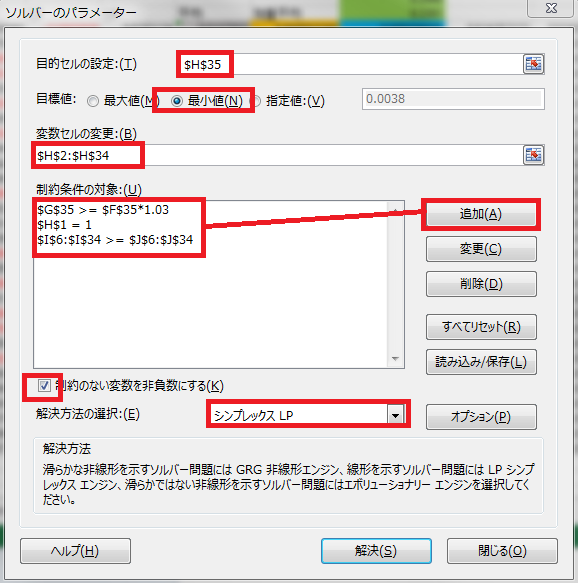
準備してきたシートをもとにソルバーで問題を解いてみます。求めるのは投資配分比率で、エクセルシート上ではセルH2からH5に対応します。
前章で紹介したように、Excelのデータタブからソルバーを起動させます。ソルバーが起動したら下記の設定をします。
- 目的セル:
$H$35 - 目標値:最小値
- 変数セルの変更:
$H$2:$H$34 - 制約条件の対象には下記の3つを設定(追加ボタンより入力)
$G$35 >= $F$35 * 1.03$H$1 = 1$I$6:$I$34 >= $J$6:$J$34- 制約のない変数を非負数にするにチェックを入れる
- 解決方法の選択:シンプレックスLPを選択
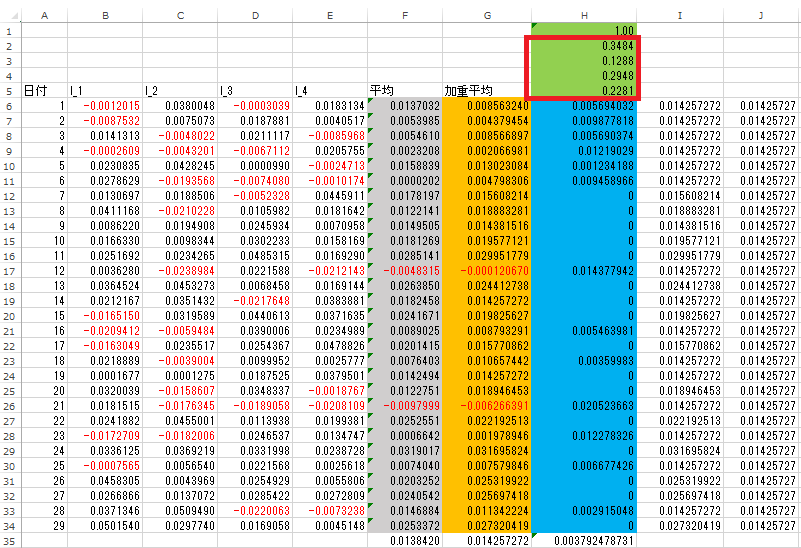
上記のように設定することが、最初に示した平均-絶対偏差モデルの定式化に等しくなっています。設定が完了したら解決ボタンを押します。問題がなければソルバーの結果(投資配分比率)がセルH2からH5に出力されます。
まとめ
本章ではExcelソルバーを使って最適化問題の一つであるポートフォリオ最適化問題を解くことを考えてきました。金融ポートフォリオ最適化モデルとしてよく知られている平均-分散モデルと平均-絶対偏差モデルの最適化問題としての定式化を紹介しました。コンパクト分解表現を使うことで元の問題が簡潔に表現可能で、特に平均-絶対偏差モデルは線形計画問題で定式化できることを紹介しました。最後に平均-絶対偏差モデルをExcelソルバーで解く紹介をしました。
本章で紹介してきたようにExcelソルバーを使うことで、簡単に制約条件付き目的関数の最小/最大を求めることができるので便利です。Excelソルバーには取り扱える変数に上限がありました。しかし、Excel上でロジックをしっかり理解しておくことは、その他のプログラミング言語でソルバーライブラリを使った実装をするときに役立ちます。ぜひExcelソルバーを活用してみてください!!
===========================================
こちらもよろしくおねがいいたします。
入門編
第1部イントロダクション
第2部エクセルで学ぶ分析入門
==================