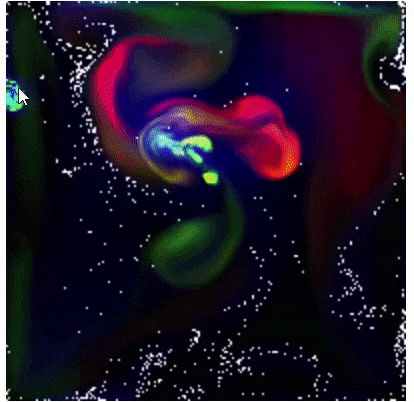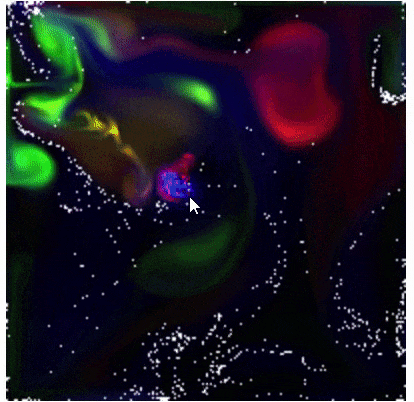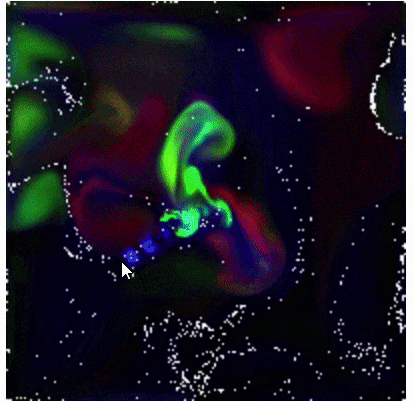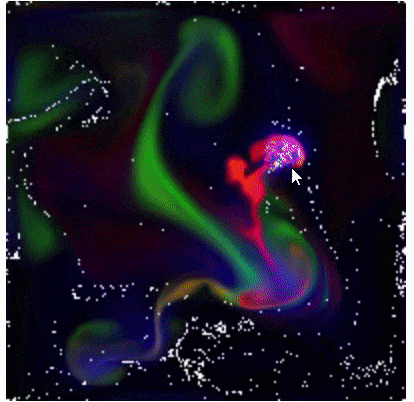
詰め込み感あるタイトルですが、そのままです。

流体シミュレーションに関しては素人なのですが、計算量が多くて、数値計算の典型的な練習問題としてよく扱われますし、 WebAssembly はまさにこんな問題に対して作られた技術だと思えるので、計算速度も見てみたいという気持ちもこめてやってみました。 ¹

成果物はブラウザだけあれば確認できますので自分で確認したいという方はこちらへどうぞ。ソースはこちらです。

せっかく Rust を使ったのですが、プログラミング言語に関する話題は出てきません。

動画

結果から言うと、下のような200x200ピクセルのアニメーション程度であればほぼリアルタイムに計算できます。まあこのくらいなら JavaScript でも最適化できるのではないかという気もします。

本稿では基本的に文献 ² に従って行きます。

非圧縮流体のナビエ・ストークス方程式

有名な奴ですね。
速度場の方程式は次のようなベクトル方程式になります。

$$\frac{\partial \mathbf{u}}{\partial t} = -(\mathbf{u} \cdot \nabla) \mathbf{u} - \nu \nabla^2 \mathbf{u} + \mathbf{f} $$

非圧縮とはいうのですが、流体の動きが見えないと面白くないので、 dye (染料)を速度場に乗せて流します。この染料の密度が従う方程式は次です。

$$\frac{\partial \rho}{\partial t} = -(\mathbf{u} \cdot \nabla) \rho + \kappa \nabla^2 \rho + S$$

シミュレータの仕事は、この偏微分方程式を数値的に解く、別の言い方をすると数値積分するということです。

拡散項

この論文では拡散項のソルバーが繰り返し出てくるのですが、その実装に至った経緯を理解するのが一番の難関でした。

拡散項とは $\nabla^2 a$ のような項のことで、スカラー場のラプラシアンの形をしています。上記のナビエ・ストークス方程式では速度と染料の拡散項が出てきます。特に速度の拡散項は粘性を表すものであり、カルマン渦をシミュレートするには重要です。

普通に考えると、ラプラシアンの離散化は次のように周囲の4セルの差分になると思います。ここでxは次のステップでの場の値、x0は前のステップの値です。

x(i,j) = x(i,j) + a * (x0(i-1,j) + x0(i+1,j) + x0(i,j-1) + x0(i,j+1) - 4*x0(i,j))

しかしながら、この方法で更新するのはうまくいきません。拡散速度の係数 a が1より大きくなると、発振して絶対値が無限大に発散してしまうのです。つまりこの更新ルールは不安定なのです。

と、まあここまでは理解できたのです。実際この方法で実装してみると発散しますし、他の数値計算の問題でも不安定なソルバーが発散するのはよく経験しますので。

しかし、唐突に次のような更新ルールであれば安定であるということが示されます。

x0(i,j) = x(i,j) - a * (x(i-1,j) + x(i+1,j) + x(i,j-1) + x(i,j+1) - 4*x(i,j))

現在の値x0を元に未来の値xを計算するのではなく、未来の値xから現在の値x0を計算するという式です。
これは微分を離散化したものなので、 $t$ だろうが $t+\Delta t$ だろうが極限は同じなわけですが、なぜこの方が安定するのか、その論理がまったくわかりません。

その後の調べで、これはおそらく Implicit method といわれるアプローチだろうという推論に落ち着きました。

Implicit method

Implicit method とは Explicit method に対する対義語です。 Explicit method は、現在の状態 $Y(t)$ からのみ次のタイムステップ $Y(t+1)$ を計算するという、いわゆる陽に解くということです。

$$Y(t+1) = F(Y(t))$$

しかしながら、この方法は誤差が累積していくという特徴があり、精度をよくするのが極めて難しいです。簡単な例でいうと太陽系の軌道シミュレータのようなものであっても、楕円軌道を安定的に描かせることすらできません³。原理的にはタイムステップを小さくしていけば精度は上がっていくわけですが、そのために必要なステップの細かさと計算量の増大は、現実的なものではありません。

Implicit method は、次式のように、次のタイムステップと現在のタイムステップをまとめて方程式を解くという方法です。 Explicit method のように右辺を単純に計算するだけでは次の状態が得られないので、一般的に複雑になります。

$$
G\big(Y(t+1), Y(t)\big) = 0
$$

この問題の場合、 Explicit method であれば次のように離散化でき(タイムステップを上付きの $(t)$ で表しています)、

\begin{align}
\frac{\partial y}{\partial t} &= \nabla^2 y \\
\frac{y^{(t+1)}_{i,j} - y^{(t)}_{i,j}}{\Delta t} &= \frac{y^{(t)}_{i-1,j} + y^{(t)}_{i+1,j} - 2y^{(t)}_{i,j}}{\Delta x} + \frac{y^{(t)}_{i,j-1} + y^{(t)}_{i,j+1} - 2y^{(t)}_{i,j}}{\Delta y} 
\end{align}

係数を $a$ にまとめると次のように書けます($\Delta x$ と $\Delta y$ は同じと見なします)。

y^{(t+1)}_{i,j} = y^{(t)}_{i,j} + a \left(y^{(t)}_{i-1,j} + y^{(t)}_{i+1,j} + y^{(t)}_{i,j-1} + y^{(t)}_{i,j+1} - 4y^{(t)}_{i,j}\right)

これに対し、 Implicit method なら次のように書けるわけです。

\frac{y^{(t+1)} - y^{(t)}}{\Delta t} = \frac{y^{(t+1)}_{i-1,j} + y^{(t+1)}_{i+1,j} - 2y^{(t+1)}_{i,j}}{\Delta x} + \frac{y^{(t+1)}_{i,j-1} + y^{(t+1)}_{i,j+1} - 2y^{(t+1)}_{i,j}}{\Delta y} \\
y^{(t+1)}_{i,j} - a \left(y^{(t+1)}_{i-1,j} + y^{(t+1)}_{i+1,j} + y^{(t+1)}_{i,j-1} + y^{(t+1)}_{i,j+1} - 4y^{(t+1)}_{i,j}\right)
= y^{(t)}_{i,j}

さて、この方程式から $y^{(t+1)}$ を解かなくてはならないわけですが、実際にはこの式は全ての $i,j \in I,J$ について同時に解かなくてはなりませんので、巨大な連立方程式になります。ここで $I,J$ はシミュレーション空間を離散化したマスの $x,y$ 方向のそれぞれの数です。
例えば、200x200のマスに区切った場合、40000個の連立方程式になるわけです。

幸運なことに、これは線形連立方程式ですので原理的には逆行列を求めれば解くことができます。

F \mathbf{y}^{(t+1)} = \mathbf{y}^{(t)} \\
\mathbf{y}^{(t+1)} = F^{-1} \mathbf{y}^{(t)}

しかし40000x40000の逆行列を解くのは現実的ではありません。そこで Gauss-Seidel 法というものを使います。詳しくはリンク先の Wikipedia の記事に丸投げしますが、このような疎な行列で、ある条件を満たせば、反復計算によって近似解を求めることができます。反復計算によって Explicit method よりもステップ当たりの計算量が何倍にもなりますが、それでも40000x40000の逆行列を求めるよりはましです。また、同じシミュレーション精度を求めるのに必要な計算量では Explicit method よりも圧倒的に勝っています。

安定性

さて、 Implicit method が安定性に関して有利である場合があるとはいえ、実際に安定化するかは問題によるそうです。これではいまいち納得がいきません。ここで次の参考動画⁴からの考え方を引用します。

まず、 Explicit method で出てきた更新ルールを単純な形に書き直します。ここで $\mathbf{s}$ は周囲のマスの平均値を表します。

$$
\mathbf{y}^{(t+1)} = \mathbf{y}^{(t)} + a(\mathbf{s}^{(t)} - \mathbf{y}^{(t)})
$$

これは、 $\mathbf{s}^{(t)}$ と $\mathbf{y}^{(t)}$ の線形補間という見方ができます。 $a<1$の間はいいのですが、$1<a$の場合はオーバーシュートしてしまいます。これこそが不安定性の根本的な原因であります。

これに対し、 Implicit method は次のようなものでした。

$$
\mathbf{y}^{(t)} = \mathbf{y}^{(t+1)} - a(\mathbf{s}^{(t+1)} - \mathbf{y}^{(t+1)})
$$

これをちょっと変形すると、

$$
\mathbf{y}^{(t+1)} = \frac{\mathbf{y}^{(t)} + a\mathbf{s}^{(t)}}{1+a}
$$

となります。これは $\mathbf{s}^{(t)}$ と $\mathbf{y}^{(t)}$ の間の補間と見なすこともできますが、線形補間ではなく、なにやら変わった補間です。 $\frac{a}{1+a}$ の値は $a$ がいくら大きくなっても $1$ を超えることはなく、漸近していくだけです。これによって安定性が確保されるというわけです。

移流 (Advection)

移流とはふつうお目にかからない単語ですが、速度ベクトルに乗って属性が運動していくことをいいます。ここでも、計算を最適化するのにひと工夫されています。現在のステップから次のステップの移動位置を求めるのではなく、次のステップの位置から、前のステップのどこから移動してきたかを求め、周囲の４ピクセルから線形補間します。ここでも時間を逆方向に見るような不思議な考え方をします。

ただ、ここの議論は原論文でもわかりやすいので省略します。前述の Implicit method が理解できる人ならつまづくこともないと思います。

発散の除去

我々は非圧縮流体を仮定しましたので、速度場の発散があっては困ります。速度場の発散があるということは、無から有が生じているか、有るものが消えてなくなっているということになります。しかし、今までの計算ではそのような制約はかけていませんでしたので、速度場には発散成分が混入してしまっています。これを除去するために、ヘルムホルツの定理を利用します。

ヘルムホルツの定理とは、任意のベクトル場は回転成分と発散成分に分解できるというものです。たとえばベクトル場 $\mathbf{F}$ は、スカラーポテンシャル $\phi$ とベクトルポテンシャル $\mathbf{A}$ を使って、次のように書けます。

\mathbf{F} = \nabla \phi + \nabla \times \mathbf{A}

スカラー場の勾配は回転成分を持たず、ベクトル場の回転は発散を持たないため、回転成分のみと発散成分のみの成分に分解できるというわけです。

回転成分を直接求めるのは簡単ではないので、まず発散成分を求め、それを元の速度場から引くことによって回転成分を抽出します。

発散成分を求めるにはまず次の式を解いて $\phi$ を求めます。ここで $\mathbf{u}$ は速度場です。

\nabla^2 \phi = \nabla \cdot \mathbf{u}

これを離散化して書くと

\frac{\phi_{i-1,j} + \phi_{i+1,j} - 2\phi_{i,j}}{\Delta x} + \frac{\phi_{i,j-1} + \phi_{i,j+1} - 2\phi_{i,j}}{\Delta y} = \frac{u_{x,i+1,j} - u_{x,i-1,j}}{\Delta x} + \frac{u_{y,i,j+1} - u_{y,i,j-1}}{\Delta y}

右辺は普通に計算できますが、それを満たす左辺はどうやって計算したらいいでしょうか。この式は $IJ$ 個の組み合わせであることを思い起こせば、すべての式を同時に解くしかないということになります。おや、何だか聞き覚えのある話ですね。

F\phi = \nabla \mathbf{u} \\
\phi = F^{-1}\nabla \mathbf{u}

ここでもまた、 Gauss-Seidel 法を使うことができます。実際、同じ関数を流用しています。

この $\phi$ から勾配を求めることによって速度場の発散成分のみ $\mathbf{u}_d$ を抽出します。

\mathbf{u}_d = \nabla \phi

この $\mathbf{u}_d$ を使って発散なし成分を次のように求めることができます。

\mathbf{u}_r = \mathbf{u} - \mathbf{u}_d

温度と対流

さて、ここからは論文から離れて、独自の拡張を施します。煮立った味噌汁の味噌が対流するやつ、あれをやってみたいということです。

対流現象とは、本来は圧力と密度の変化によるものですが、本シミュレーションでは非圧縮流体を仮定していますので、密度は変化しません。それではどうやってモデル化するのかというと、単純に「周りの温度より高い部分は浮かび上がる」「周りの温度より低い部分は沈み込む」というルールを組み込むだけです。

周りの温度より高いか、低いかというのはラプラシアンで表現できます。これに適当な係数をかけて Y 方向の速度変化にしてやれば対流が実現できます。

\frac{\partial u_y}{\partial t} = \gamma \nabla^2 T

当然、温度 $T$ も流体について回る属性ですので、今までの拡散や移流といった現象の対象になります。しかし、これはすでに染料で組んだコードなのでそのまま再利用できます。

結果、下のようなシミュレーションができました。赤は温度の高さを表します。右下に高熱源、左上に低熱源を配置しています。

おまけ

一応速度ベクトルのプロットもやってみたのですが、粒子の動きのほうがわかりやすいですね。

さらにおまけ

粒子の軌跡もプロットしてみました。

感想

流体の「なまめかしい」動きを単純なルールで再現できるのはとても気持ち良いです。しかし単純に見えるルールも、安定的にシミュレートするにはさまざまなテクニックがあり、どうやって思いついたのかわからないような工夫の塊です。流体シミュレーションの世界はまだまだ奥が深そうです。このような問題解決の発想法を身に着けたいものですが、先人の知恵と試行錯誤の結果なので、一朝一夕に身につくものではないのでしょう。

真面目に計算速度を追及するなら CUDA か OpenCL で GPU 計算するのが筋でしょうが、まあオモチャですので。 ↩
https://www.dgp.toronto.edu/public_user/stam/reality/Research/pdf/GDC03.pdf ↩
軌道シミュレータについては、 Runge-Kutta 法が適しています。 ↩
https://youtu.be/qsYE1wMEMPA?t=354 ↩

流体シミュレーションをRustでWebassemblyにしてブラウザで動かしてみた

動画