Heaviside関数を使って?２つの頂点が動点の三角形の面積計算「24年 共通テ 本試験 I 3-2・IA 2-1 2次関数の応用問題」をsympyと作図をやってみたい。

Piecewise関数が、楽でした。
・Piecewise関数とmaximum関数の組み合わせができました。
　??? できないはずです。
Represents an expression, condition pair.
https://docs.sympy.org/latest/modules/functions/elementary.html#piecewise

# ver0.4
from sympy import *
var('t',real=True,positive=True)
Vx=Point(1,0)
Vy=Point(0,1)*2
O =Point(0,0)
B =Point(4,6)
C =Point(0,6)
# 
P =Point(1,0)*t
BQP=Piecewise((Triangle(B,C-Vy*t,P).area,t<3),(Triangle(B,O+Vy*(t-3),P).area,True))
# 
print("# (1)ア    ",        BQP.subs({t:0})     )
print("# (2)イ    ",minimum(BQP,t,Interval(0,3)))
print("# (2)ウエ  ",maximum(BQP,t,Interval(0,3)))
print("# (3)オ    ",minimum(BQP,t,Interval(0,6)))
print("# (3)カキ  ",maximum(BQP,t,Interval(0,6)))
sol=solveset(Le(BQP,10),t,Interval(0,6))     
print("# (4)クケコ",sol.args[1]-sol.args[0])
# (1)ア     12
# (2)イ     8
# (2)ウエ   12
# (3)オ     8
# (3)カキ   13
# (4)クケコ -sqrt(3) + sqrt(2) + 3
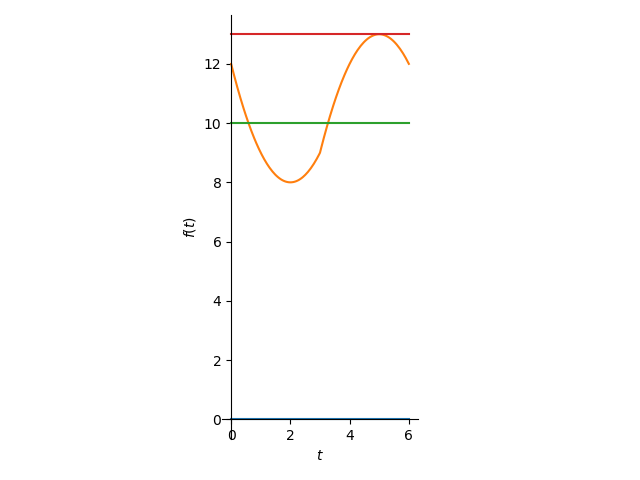
from sympy.plotting import plot
plot(0,BQP,10,13,(t,0,6),aspect_ratio=(1.0,1.0))

以下は、旧です。

旧タイトル)　Heaviside関数を使って?動点が２つの三角形の面積計算「24年 共通テ 本試験 I 3-2・IA 2-1 2次関数の応用問題」をsympyと作図をやってみたい。2024/02/03

・Heaviside関数は、入試範囲外のはずです。
　??? ヘビサイドの展開定理 | 高校数学の美しい物語
・Heaviside関数は、もしかしたら、大学工学系1,2年生のオニイサン、オネエサンの関数だと思います、
　
パイソニスタの方へ
・Heaviside関数の正しい?使い方を教えて下さい。　　 　
　(ver0.2)プログラムは、3秒後、下へ行き過ぎ。
　速度2tを足して水平にしました。さらに、2tを足しました。 追加2024/02/02
　(ver0.1)プログラムは、3秒後から、倍のスピード4tを足しています。
　グラフが、3秒後速度2tで右下さがりだから、4tで上げています。
・Ropenで分割しています。Ropenを使わない方法がありますか？
　solveset関数はできるのに、maximum関数は、できませんでした。
・Singularity functionで、できそうですか？

(参考)
・sympyで「Heaviside step function(ヘヴィサイドの階段関数)」を使ってみた
https://qiita.com/mrrclb48z/items/ef607bd4016bb2541e55#sympy%E3%81%A7
・sympyで「Singularity function(特異関数)」を使ってみた
https://qiita.com/mrrclb48z/items/9e776ca8f365a7a36fc3

オリジナル　

　数学入試問題 様

　上と同じです。大学入試数学問題集成 様＞テキスト 【２】［１］

T氏の数学日記 様
　＞...２つの動点...
　https://mathmathmass.exblog.jp/33659035/

掲示板より ＜ 大学入試数学問題集成 様　
　私の自作の会話あり。小学6年生のタツ郎先生登場。
　https://mathexamtest.bbs.fc2.com/
　24年 共通テ 本試験 I 3-2・IA 2-1　2次関数の応用問題 その1
　2024/01/23 (Tue) 13:00:47 より

sympyのplot関数で作図(Heaviside関数を使って)

・ver0.3。
・Ropen,Lopenは、解決していません。(2024/02/15)
・Heaviside関数を使って、ひとつにできないので、最大値２つの比較です。

# ver0.3
from sympy import *
var('t',real=True)
BQP_03=Triangle((4, 6),(0, 6-t*2  ),(t, 0)).area
BQP_36=Triangle((4, 6),(0, (t-3)*2),(t, 0)).area
BQP   =BQP_03-Heaviside(t-3,H0=1)*BQP_03+Heaviside(t-3,H0=1)*BQP_36
# 
print("# (1)ア    ",        BQP.subs({t:1})           )
print("# (2)イ    ",minimum(BQP,t,Interval.Ropen(0,3)))
print("# (2)ウエ  ",maximum(BQP,t,Interval.Ropen(0,3)))
# print("# (3)オ    ",minimum(BQP,t,Interval(0,6)))
# print("# (3)カキ  ",maximum(BQP,t,Interval(0,6)))
print("# (3)オ    ",min( minimum(BQP,t,Interval.Ropen(0,3)),minimum(BQP,t,Interval.Lopen(3,6))))
print("# (3)カキ  ",max( maximum(BQP,t,Interval.Ropen(0,3)),maximum(BQP,t,Interval.Lopen(3,6))))
sol=solveset(Le(BQP,10),t,Interval(0,6))      
print("# (4)クケコ",sol.args[1]-sol.args[0])
# (1)ア     9
# (2)イ     8
# (2)ウエ   12
# (3)オ     8
# (3)カキ   13
# (4)クケコ -sqrt(3) + sqrt(2) + 3

print("#",BQP_03.subs({t:3}))
print("#",BQP_36.subs({t:3}))
print("#",BQP   .subs({t:3}))
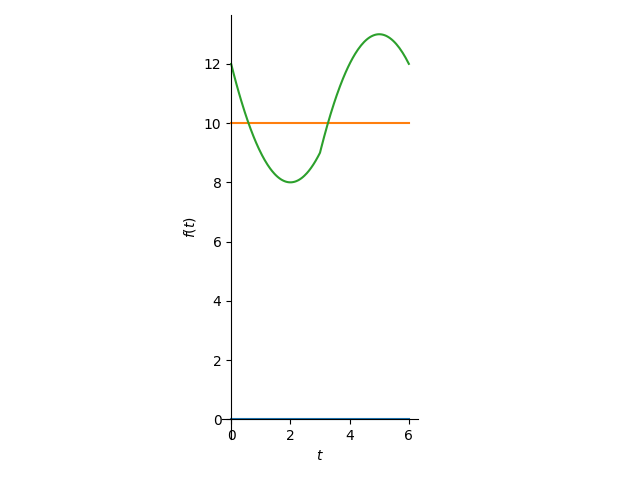
from sympy.plotting import plot
plot(0,10,BQP,(t,0,6),aspect_ratio=(1.0,1.0))
# 9
# 9
# 9

sympyで(Heaviside関数を使って)

・ver0.2。sympy風にしました。ver0.1と同じです。

# ver0.2
from sympy import *
var('t',real=True,positive=True )
Vx=Point(1,0)
Vy=Point(0,1)
B =Point(4,6)
C =Point(0,6)
P =Point(1,0)*t
t3=3
Q =C-2*Vy*t+Heaviside(t-t3,H0=0)*2*Vy*(t-t3)  +Heaviside(t-t3,H0=0)*2*Vy*(t-t3)
BQP=Triangle(B,Q,P).area           
# 
print("# (1)ア    ",BQP.subs({t:0}))
# print("# (2)イ  ",    minimum(BQP,t,Interval(0,t3)))
# print("# (2)ウエ",    maximum(BQP,t,Interval(0,t3)))
print("# (2)イ    ",    minimum(BQP,t,Interval.Ropen(0,t3)))
print("# (2)ウエ  ",    maximum(BQP,t,Interval.Ropen(0,t3)))
print("# (3)オ    ",min(minimum(BQP,t,Interval.Ropen(0,t3)),minimum(BQP,t,Interval.Lopen(t3,6))))
print("# (3)カキ  ",max(maximum(BQP,t,Interval.Ropen(0,t3)),maximum(BQP,t,Interval.Lopen(t3,6))))
sol=solveset(Le(BQP,10),t,Interval(0,6))        # ;print("# sol=",sol)
print("# (4)クケコ",sol.args[1]-sol.args[0])
# (1)ア     12
# (2)イ     8
# (2)ウエ   12
# (3)オ     8
# (3)カキ   13
# (4)クケコ -sqrt(3) + sqrt(2) + 3

・ver0.1

# ver0.1
from sympy import *
var('t',real=True,positive=True )
OC =6
Psp=1
Qsp=2
t3 =Rational(OC,Qsp)
Qy =OC-Qsp*t*Heaviside(t-0,H0=0)+2*Qsp*(t-t3)*Heaviside(t-t3,H0=0)  #;print("# Qy=",Qy  )
BQP=Triangle(Point(4,6),Point(0,Qy),Point(Psp*t,0)).area            #;print("# BQP",BQP)
# 
print("# (1)ア    ",BQP.subs({t:0}))
# print("# (2)イ  ",    minimum(BQP,t,Interval(0,t3)))
# print("# (2)ウエ",    maximum(BQP,t,Interval(0,t3)))
print("# (2)イ    ",    minimum(BQP,t,Interval.Ropen(0,t3)))
print("# (2)ウエ  ",    maximum(BQP,t,Interval.Ropen(0,t3)))
print("# (3)オ    ",min(minimum(BQP,t,Interval.Ropen(0,t3)),minimum(BQP,t,Interval.Lopen(t3,6))))
print("# (3)カキ  ",max(maximum(BQP,t,Interval.Ropen(0,t3)),maximum(BQP,t,Interval.Lopen(t3,6))))
sol=solveset(Le(BQP,10),t,Interval(0,6))        # ;print("# sol=",sol)
print("# (4)クケコ",sol.args[1]-sol.args[0])
# (1)ア     12
# (2)イ     8
# (2)ウエ   12
# (3)オ     8
# (3)カキ   13
# (4)クケコ -sqrt(3) + sqrt(2) + 3

sympyで(オリジナル 様を参考に)

・以下は、Heaviside関数を使っていません。
・A polygon with three vertices and three sides.
https://docs.sympy.org/latest/modules/geometry/polygons.html#sympy.geometry.polygon.Triangle
・小技。10を10.0にすると、小数点表示になります。困りました。

・ver0.1

# ver0.1
from sympy import *
var('t' ,real=True,positive=True)
var('Qy',real=True,positive=True)
OC =6
Psp=1
Qsp=2
t3 =Rational(OC,Qsp)
# 
PBQ_t03=Triangle(Point(Psp*t,0),Point(4,6),Point(0,6-2*t)).area   #;print("# PBQ_t03",PBQ_t03)
PBQ_t36=Triangle(Point(Psp*t,0),Point(4,6),Point(0,2*t-6)).area   #;print("# PBQ_t36",PBQ_t36)
print("# (1)ア    ",PBQ_t03.subs({t:1}))
print("# (2)イ    ",    minimum(PBQ_t03,t,Interval(0,t3)))
print("# (2)ウエ  ",    maximum(PBQ_t03,t,Interval(0,t3)))
print("# (3)オ    ",min(minimum(PBQ_t03,t,Interval(0,t3)),minimum(PBQ_t36,t,Interval(t3,6))))
print("# (3)カキ  ",max(maximum(PBQ_t03,t,Interval(0,t3)),maximum(PBQ_t36,t,Interval(t3,6))))
sol1= solveset(Eq(PBQ_t03,10),t,Interval(0 ,t3)).args[0] ;print("# sol1=",sol1)
sol2= solveset(Eq(PBQ_t36,10),t,Interval(t3,6 )).args[0] ;print("# sol2=",sol2)
print("# (4)クケコ",sol2-sol1)
# (1)ア     9
# (2)イ     8
# (2)ウエ   12
# (3)オ     8
# (3)カキ   13
# sol1= 2 - sqrt(2)
# sol2= 5 - sqrt(3)
# (4)クケコ -sqrt(3) + sqrt(2) + 3

作図

・グラフの勉強中。Heaviside関数は、plot関数が使えるはず？です。
・FreeCADの勉強中

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

いつもと違うおすすめです。

過去問の類題

・梁の？影響線に似ていますか。

・ゼロスタート、ゼロエンド(表現は別件より)

・いつもの自転車君のゆうどうです。
2022年数列に似ていると、思いました。
https://qiita.com/mrrclb48z/items/297442a71820732d3ea3

別件の別件

＞google検索 直線定規でヒットします。